Tri de 1 million de nombres à 8 chiffres en 1 Mo de mémoire vive

Il y a un truc pas mentionné jusqu'ici. Nous supposons que vous n'avez aucun moyen de stocker des données, mais qui n'est pas strictement vrai.

une façon de contourner votre problème est de faire l'horrible chose suivante, qui ne devrait être tentée par personne dans n'importe quelles circonstances: utiliser le trafic réseau pour stocker des données. Et Non, Je ne veux pas dire NAS.

, Vous pouvez trier les nombres avec seulement quelques octets de RAM de la façon suivante:

• première prise 2 variables: COUNTER et VALUE .
• premier ensemble de tous les registres à 0 ;
• chaque fois que vous recevez un entier I , increment COUNTER et mettez VALUE à max(VALUE, I) ;
• envoie ensuite au routeur un paquet ICMP echo request avec les données définies à I. Effacer et je le répète.
• chaque fois que vous recevez le retour ICMP packet, vous extrayez simplement l'entier et le renvoyez à nouveau dans une autre requête echo. Cela produit un nombre énorme de requêtes ICMP contenant les nombres entiers.

une fois COUNTER atteint 1000000 , vous avez toutes les valeurs stockées dans le flux incessant des requêtes ICMP, et VALUE contient maintenant l'entier maximum. Choisis threshold T >> 1000000 . Mettez COUNTER à zéro. Chaque fois que vous recevez une ICMP paquet, incrémenter COUNTER et envoyer l'entier contenu I revenir dans une autre requête echo, sauf si I=VALUE , dans ce cas transmettre à la destination pour les entiers triés. Une fois COUNTER=T , décrément VALUE par 1 , réinitialisez COUNTER à zéro et répétez. Une fois que VALUE atteint zéro, vous devriez avoir transmis tous les entiers dans l'ordre de la plus grande à la plus petite à la destination, et n'avoir utilisé qu'environ 47 bits de RAM pour les deux variables persistantes. (et tout petit montant dont vous avez besoin pour les valeurs temporaires).

je sais que c'est horrible, et je sais qu'il peut y avoir toutes sortes de problèmes pratiques, mais j'ai pensé que cela pourrait faire rire certains d'entre vous ou au moins vous horrifier.

voici du code C++ qui résout le problème.

preuve que les contraintes de mémoire sont satisfaites:

Éditeur: Il n'y a aucune preuve de la capacité de mémoire maximale exigences offert par l'auteur, soit dans ce post ou dans ses blogs. Depuis le nombre de bits nécessaires pour coder une valeur dépend des valeurs précédemment codé, une telle preuve est susceptible non-trivial. L'auteur note que la plus grande taille encodée sur laquelle il pouvait tomber empiriquement était 1011732 , et a choisi la taille de tampon 1013000 arbitrairement.

typedef unsigned int u32;

namespace WorkArea
{
    static const u32 circularSize = 253250;
    u32 circular[circularSize] = { 0 };         // consumes 1013000 bytes

    static const u32 stageSize = 8000;
    u32 stage[stageSize];                       // consumes 32000 bytes

    ...

ensemble, ces deux tableaux prennent 1045000 octets de stockage. Il reste 1048576 - 1045000 - 2×1024 = 1528 octets pour les variables restantes et l'espace de pile.

il court en 23 secondes sur mon Xeon W3520. Vous pouvez vérifier que le programme fonctionne en utilisant le Python suivant script, assumant un nom de programme de sort1mb.exe .

from subprocess import *
import random

sequence = [random.randint(0, 99999999) for i in xrange(1000000)]

sorter = Popen('sort1mb.exe', stdin=PIPE, stdout=PIPE)
for value in sequence:
    sorter.stdin.write('%08d\n' % value)
sorter.stdin.close()

result = [int(line) for line in sorter.stdout]
print('OK!' if result == sorted(sequence) else 'Error!')

une explication détaillée de l'algorithme peut être trouvée dans la série suivante de messages:

• 1MB Tri expliqué
• Codage Arithmétique et la 1MB Problème de Tri
• Codage Arithmétique Utilisant Les Mathématiques À Point Fixe

consultez première bonne réponse ou le plus tard réponse à l'arithmétique codage . ci-dessous vous pouvez trouver un peu de plaisir, mais pas une solution 100% pare-balles.

c'est une tâche assez intéressante et voici une autre solution. J'espère que quelqu'un trouvera le résultat utile (ou du moins intéressant).

Étape 1: structure initiale des données, approximative méthode de compression, résultats de base

faisons quelques mathématiques simples: nous avons 1m (1048576 octets) de RAM initialement disponible pour stocker 10^6 nombres décimaux à 8 chiffres. [0; 99999999]. Donc, pour stocker un nombre 27 bits sont nécessaires (en partant de l'hypothèse que les numéros non signés seront utilisés). Ainsi, pour stocker un flux brut ~3,5 m de RAM sera nécessaire. Quelqu'un a déjà dit que cela ne semblait pas faisable, mais je dirais que la tâche peut être résolue si l'entrée est "assez bonne". Fondamentalement, l'idée est de compresser les données d'entrée avec un facteur de compression de 0,29 ou plus et faire le tri dans une manière appropriée.

résolvons d'abord le problème de la compression. Certains tests pertinents sont déjà disponibles:

http://www.theeggeadventure.com/wikimedia/index.php/Java_Data_Compression

" j'ai fait un test pour compresser un million d'entiers consécutifs en utilisant diverses formes de compression. Les résultats sont les suivants:"

None     4000027
Deflate  2006803
Filtered 1391833
BZip2    427067
Lzma     255040

il ressemble à LZMA ( Lempel–Ziv–Markov chaîne algorithme ) est un bon choix pour continuer. J'ai préparé un simple PoC, mais il y a encore quelques détails à mettre en évidence:

1. la mémoire est limitée de sorte que l'idée est de présenter des nombres et d'utiliser seaux comprimés (dimension dynamique) en stockage temporaire
2. il est plus facile d'obtenir un meilleur facteur de compression avec données, il y a donc une mémoire tampon statique pour chaque seau (les nombres de la mémoire tampon doivent être triés avant LZMA)
3. chaque seau contient une gamme spécifique, de sorte que le tri final peut être fait pour chaque seau séparément
4. la taille du seau peut être correctement réglée, donc il y aura assez de mémoire pour décompresser les données stockées et faire le tri final pour chaque seau séparément

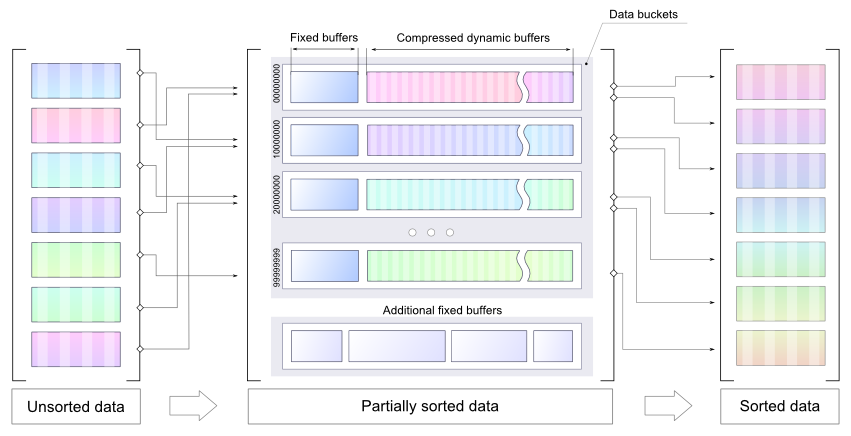
s'il vous Plaît noter, attaché de code est un POC , il ne peut pas être utilisé comme une solution définitive, il démontre simplement l'idée d'utiliser plusieurs petits tampons pour stocker le tri préalable des nombres dans certains de façon optimale (éventuellement compressé). La LZMA n'est pas proposée comme solution définitive. Il est utilisé comme un moyen le plus rapide possible d'introduire une compression à ce PoC.

voir le code PoC ci-dessous (s'il vous plaît noter juste une démo, pour la compilation LZMA-Java seront nécessaires):

public class MemorySortDemo {

static final int NUM_COUNT = 1000000;
static final int NUM_MAX   = 100000000;

static final int BUCKETS      = 5;
static final int DICT_SIZE    = 16 * 1024; // LZMA dictionary size
static final int BUCKET_SIZE  = 1024;
static final int BUFFER_SIZE  = 10 * 1024;
static final int BUCKET_RANGE = NUM_MAX / BUCKETS;

static class Producer {
    private Random random = new Random();
    public int produce() { return random.nextInt(NUM_MAX); }
}

static class Bucket {
    public int size, pointer;
    public int[] buffer = new int[BUFFER_SIZE];

    public ByteArrayOutputStream tempOut = new ByteArrayOutputStream();
    public DataOutputStream tempDataOut = new DataOutputStream(tempOut);
    public ByteArrayOutputStream compressedOut = new ByteArrayOutputStream();

    public void submitBuffer() throws IOException {
        Arrays.sort(buffer, 0, pointer);

        for (int j = 0; j < pointer; j++) {
            tempDataOut.writeInt(buffer[j]);
            size++;
        }            
        pointer = 0;
    }

    public void write(int value) throws IOException {
        if (isBufferFull()) {
            submitBuffer();
        }
        buffer[pointer++] = value;
    }

    public boolean isBufferFull() {
        return pointer == BUFFER_SIZE;
    }

    public byte[] compressData() throws IOException {
        tempDataOut.close();
        return compress(tempOut.toByteArray());
    }        

    private byte[] compress(byte[] input) throws IOException {
        final BufferedInputStream in = new BufferedInputStream(new ByteArrayInputStream(input));
        final DataOutputStream out = new DataOutputStream(new BufferedOutputStream(compressedOut));

        final Encoder encoder = new Encoder();
        encoder.setEndMarkerMode(true);
        encoder.setNumFastBytes(0x20);
        encoder.setDictionarySize(DICT_SIZE);
        encoder.setMatchFinder(Encoder.EMatchFinderTypeBT4);

        ByteArrayOutputStream encoderPrperties = new ByteArrayOutputStream();
        encoder.writeCoderProperties(encoderPrperties);
        encoderPrperties.flush();
        encoderPrperties.close();

        encoder.code(in, out, -1, -1, null);
        out.flush();
        out.close();
        in.close();

        return encoderPrperties.toByteArray();
    }

    public int[] decompress(byte[] properties) throws IOException {
        InputStream in = new ByteArrayInputStream(compressedOut.toByteArray());
        ByteArrayOutputStream data = new ByteArrayOutputStream(10 * 1024);
        BufferedOutputStream out = new BufferedOutputStream(data);

        Decoder decoder = new Decoder();
        decoder.setDecoderProperties(properties);
        decoder.code(in, out, 4 * size);

        out.flush();
        out.close();
        in.close();

        DataInputStream input = new DataInputStream(new ByteArrayInputStream(data.toByteArray()));
        int[] array = new int[size];
        for (int k = 0; k < size; k++) {
            array[k] = input.readInt();
        }

        return array;
    }
}

static class Sorter {
    private Bucket[] bucket = new Bucket[BUCKETS];

    public void doSort(Producer p, Consumer c) throws IOException {

        for (int i = 0; i < bucket.length; i++) {  // allocate buckets
            bucket[i] = new Bucket();
        }

        for(int i=0; i< NUM_COUNT; i++) {         // produce some data
            int value = p.produce();
            int bucketId = value/BUCKET_RANGE;
            bucket[bucketId].write(value);
            c.register(value);
        }

        for (int i = 0; i < bucket.length; i++) { // submit non-empty buffers
            bucket[i].submitBuffer();
        }

        byte[] compressProperties = null;
        for (int i = 0; i < bucket.length; i++) { // compress the data
            compressProperties = bucket[i].compressData();
        }

        printStatistics();

        for (int i = 0; i < bucket.length; i++) { // decode & sort buckets one by one
            int[] array = bucket[i].decompress(compressProperties);
            Arrays.sort(array);

            for(int v : array) {
                c.consume(v);
            }
        }
        c.finalCheck();
    }

    public void printStatistics() {
        int size = 0;
        int sizeCompressed = 0;

        for (int i = 0; i < BUCKETS; i++) {
            int bucketSize = 4*bucket[i].size;
            size += bucketSize;
            sizeCompressed += bucket[i].compressedOut.size();

            System.out.println("  bucket[" + i
                    + "] contains: " + bucket[i].size
                    + " numbers, compressed size: " + bucket[i].compressedOut.size()
                    + String.format(" compression factor: %.2f", ((double)bucket[i].compressedOut.size())/bucketSize));
        }

        System.out.println(String.format("Data size: %.2fM",(double)size/(1014*1024))
                + String.format(" compressed %.2fM",(double)sizeCompressed/(1014*1024))
                + String.format(" compression factor %.2f",(double)sizeCompressed/size));
    }
}

static class Consumer {
    private Set<Integer> values = new HashSet<>();

    int v = -1;
    public void consume(int value) {
        if(v < 0) v = value;

        if(v > value) {
            throw new IllegalArgumentException("Current value is greater than previous: " + v + " > " + value);
        }else{
            v = value;
            values.remove(value);
        }
    }

    public void register(int value) {
        values.add(value);
    }

    public void finalCheck() {
        System.out.println(values.size() > 0 ? "NOT OK: " + values.size() : "OK!");
    }
}

public static void main(String[] args) throws IOException {
    Producer p = new Producer();
    Consumer c = new Consumer();
    Sorter sorter = new Sorter();

    sorter.doSort(p, c);
}
}

avec des nombres aléatoires il produit ce qui suit:

bucket[0] contains: 200357 numbers, compressed size: 353679 compression factor: 0.44
bucket[1] contains: 199465 numbers, compressed size: 352127 compression factor: 0.44
bucket[2] contains: 199682 numbers, compressed size: 352464 compression factor: 0.44
bucket[3] contains: 199949 numbers, compressed size: 352947 compression factor: 0.44
bucket[4] contains: 200547 numbers, compressed size: 353914 compression factor: 0.44
Data size: 3.85M compressed 1.70M compression factor 0.44

pour une simple séquence ascendante (un seau est utilisé) il produit:

bucket[0] contains: 1000000 numbers, compressed size: 256700 compression factor: 0.06
Data size: 3.85M compressed 0.25M compression factor 0.06

MODIFIER

Conclusion:

1. N'essayez pas de tromper le Nature
2. utiliser une compression plus simple avec une empreinte mémoire plus faible
3. quelques indices supplémentaires sont vraiment nécessaires. Il ne semble pas possible de trouver une solution commune à l'épreuve des balles.

Phase 2: compression renforcée, conclusion finale

comme il a déjà été mentionné dans la section précédente, toute technique de compression appropriée peut être utilisée. So let's get se débarrasser de LZMA en faveur d'une approche plus simple et meilleure (si possible). Il y a beaucoup de bonnes solutions, y compris codage arithmétique , arbre Radix etc.

quoi qu'il en soit, le schéma d'encodage simple mais utile sera plus illustratif qu'une autre bibliothèque externe, fournissant un algorithme astucieux. La solution actuelle est assez simple: puisqu'il y a des seaux avec des données partiellement triées, les deltas peuvent être utilisés au lieu de nombre.

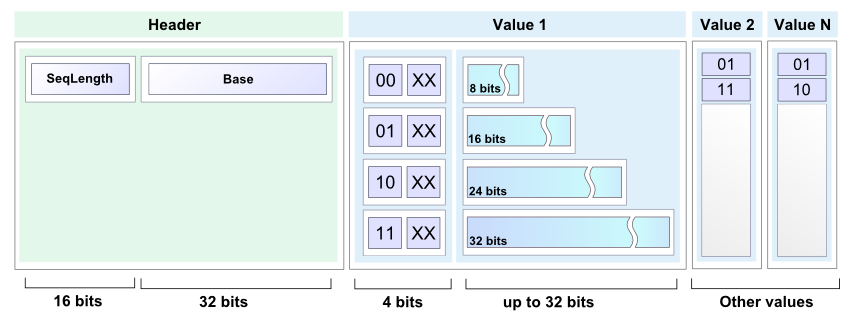
le test D'entrée aléatoire donne des résultats légèrement meilleurs:

bucket[0] contains: 10103 numbers, compressed size: 13683 compression factor: 0.34
bucket[1] contains: 9885 numbers, compressed size: 13479 compression factor: 0.34
...
bucket[98] contains: 10026 numbers, compressed size: 13612 compression factor: 0.34
bucket[99] contains: 10058 numbers, compressed size: 13701 compression factor: 0.34
Data size: 3.85M compressed 1.31M compression factor 0.34

code échantillon

  public static void encode(int[] buffer, int length, BinaryOut output) {
    short size = (short)(length & 0x7FFF);

    output.write(size);
    output.write(buffer[0]);

    for(int i=1; i< size; i++) {
        int next = buffer[i] - buffer[i-1];
        int bits = getBinarySize(next);

        int len = bits;

        if(bits > 24) {
          output.write(3, 2);
          len = bits - 24;
        }else if(bits > 16) {
          output.write(2, 2);
          len = bits-16;
        }else if(bits > 8) {
          output.write(1, 2);
          len = bits - 8;
        }else{
          output.write(0, 2);
        }

        if (len > 0) {
            if ((len % 2) > 0) {
                len = len / 2;
                output.write(len, 2);
                output.write(false);
            } else {
                len = len / 2 - 1;
                output.write(len, 2);
            }

            output.write(next, bits);
        }
    }
}

public static short decode(BinaryIn input, int[] buffer, int offset) {
    short length = input.readShort();
    int value = input.readInt();
    buffer[offset] = value;

    for (int i = 1; i < length; i++) {
        int flag = input.readInt(2);

        int bits;
        int next = 0;
        switch (flag) {
            case 0:
                bits = 2 * input.readInt(2) + 2;
                next = input.readInt(bits);
                break;
            case 1:
                bits = 8 + 2 * input.readInt(2) +2;
                next = input.readInt(bits);
                break;
            case 2:
                bits = 16 + 2 * input.readInt(2) +2;
                next = input.readInt(bits);
                break;
            case 3:
                bits = 24 + 2 * input.readInt(2) +2;
                next = input.readInt(bits);
                break;
        }

        buffer[offset + i] = buffer[offset + i - 1] + next;
    }

   return length;
}

veuillez noter, cette approche:

1. ne consomme pas beaucoup de mémoire
2. fonctionne avec des flux
3. fournit des résultats pas si mauvais

Full le code peut être trouvé ici , les implémentations BinaryInput et BinaryOutput peuvent être trouvées ici

conclusion finale

pas de conclusion finale :) parfois, il est vraiment une bonne idée de déplacer un niveau et de revoir la tâche à partir d'un méta-niveau point de vue.

c'était amusant de passer du temps avec cette tâche. BTW, Il ya beaucoup des réponses intéressantes ci-dessous. Je vous remercie de votre attention et de votre accueil chaleureux.

la réponse de Gilmanov est très erronée dans ses hypothèses. Il commence à spéculer basé sur une inutile mesure d'un million suite entiers. Cela signifie pas de lacunes. Ces écarts aléatoires, si petits soient-ils, en font vraiment une mauvaise idée.

essayez vous-même. Obtenez 1 million de nombres entiers aléatoires de 27 bits, triez-les , compressez avec 7-Zip , xz, tout LZMA que vous voulez. Le résultat est supérieur à 1,5 MB. La prémisse sur le haut est la compression des nombres séquentiels. Même delta codant de ce qui est sur 1.1 MB . Et peu importe, ceci utilise plus de 100 Mo de RAM pour la compression. Donc même les entiers compressés ne correspondent pas au problème et peu importe l'utilisation de la mémoire vive .

c'est triste de voir que les gens aiment les graphismes et la rationalisation.

#include <stdint.h>
#include <stdlib.h>
#include <time.h>

int32_t ints[1000000]; // Random 27-bit integers

int cmpi32(const void *a, const void *b) {
    return ( *(int32_t *)a - *(int32_t *)b );
}

int main() {
    int32_t *pi = ints; // Pointer to input ints (REPLACE W/ read from net)

    // Fill pseudo-random integers of 27 bits
    srand(time(NULL));
    for (int i = 0; i < 1000000; i++)
        ints[i] = rand() & ((1<<27) - 1); // Random 32 bits masked to 27 bits

    qsort(ints, 1000000, sizeof (ints[0]), cmpi32); // Sort 1000000 int32s

    // Now delta encode, optional, store differences to previous int
    for (int i = 1, prev = ints[0]; i < 1000000; i++) {
        ints[i] -= prev;
        prev    += ints[i];
    }

    FILE *f = fopen("ints.bin", "w");
    fwrite(ints, 4, 1000000, f);
    fclose(f);
    exit(0);

}

compresse maintenant les ints.bin avec LZMA...

$ xz -f --keep ints.bin       # 100 MB RAM
$ 7z a ints.bin.7z ints.bin   # 130 MB RAM
$ ls -lh ints.bin*
    3.8M ints.bin
    1.1M ints.bin.7z
    1.2M ints.bin.xz

je pense qu'une façon de penser à ce sujet est d'un point de vue combinatoire: combien de combinaisons possibles de commandes de nombres triés y a-t-il? Si nous donnons la combinaison 0,0,0,....,0 le code 0, et 0,0,0,...1 ,le code 1, et 99999999, 99999999, ... 99999999 le code N, qu'est-ce que N? En d'autres termes, quelle est la raison de l'espace?

Eh bien, une façon de penser à ce sujet est de remarquer qu'il s'agit d'une bijection du problème de trouver le nombre de chemins monotones dans un N X M grille, où N = 1 000 000 et M = 100 000 000. En d'autres termes, si vous avez une grille qui est de 1.000.000 de large et 100.000.000 de haut, combien de chemins Les plus courts du bas gauche au haut droit sont là? Les chemins Les plus courts exigent bien sûr que vous ne vous déplaciez que vers la droite ou vers le haut (si vous vous déplaciez vers le bas ou vers la gauche, vous annuleriez le progrès déjà accompli). Pour voir comment c'est une bijection de notre problème de tri des nombres, observez ce qui suit:

Vous pouvez imaginer jambe horizontale dans notre chemin comme un nombre dans notre ordre, où la position Y de la jambe représente la valeur.

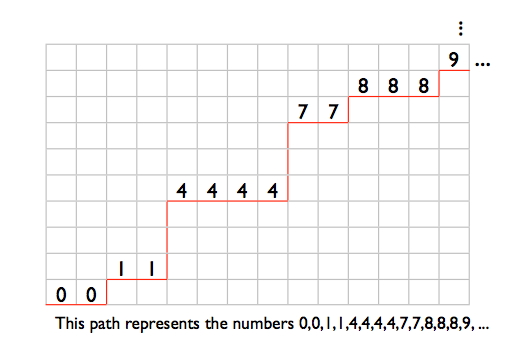
donc si le chemin se déplace simplement à droite tout le chemin jusqu'à la fin, puis saute tout le chemin vers le haut, qui est équivalent à l'ordre 0,0,...De 0. si elle commence plutôt par sauter tout le chemin vers le haut et puis se déplace vers la droite 1 000 000 de fois, qui est équivalent à 999999999999999999999,..., 99999999. Un le chemin où il se déplace droit une fois, puis vers le haut une fois, puis à droite une fois, puis vers le haut une fois, etc à la toute fin (puis saute nécessairement tout le chemin vers le haut), est équivalent à 0,1,2,3,...,999999.

heureusement pour nous ce problème a déjà été résolu, une telle grille A (N + M) choisir (M) chemins:

(1,000,000 + 100,000,000) choisir (100,000,000) ~= 2.27 * 10^2436455

N est donc égal à 2,27 * 10^2436455, et donc le code 0 représente 0,0,0,...,0 et le code 2.27 * 10^2436455 et certaines modifications représentent 9999999999999,..., 99999999.

pour stocker tous les numéros de 0 à 2.27 * 10^2436455 vous avez besoin de lg2 (2.27 * 10^2436455) = 8.0937 * 10^6 bits.

1 mégaoctet = 8388608 bits > 8093700 bits

il semble donc que nous avons au moins assez de place pour stocker le résultat! Maintenant, bien sûr, le point intéressant est de faire le tri comme le flux de nombres dans. Pas sûr que la meilleure approche à ce sujet est donné que nous avons 294908 bits restants. J'imagine qu'une technique intéressante serait de supposer à chaque point qu'il s'agit de l'Ordre Entier, trouver le code pour cet ordre, et puis comme vous recevez un nouveau nombre remontant et mettant à jour le code précédent. La main de vague de vague de la main.

Mes suggestions ici doivent beaucoup à de Dan solution

tout d'abord, je suppose que la solution doit traiter toutes les listes d'entrées possibles. Je pense que les réponses ne font pas cette hypothèse (qui l'OMI est une énorme erreur).

on sait qu'aucune forme de compression sans perte ne réduira la taille de toutes les entrées.

Toutes les réponses supposer qu'ils seront en mesure d'appliquer compression assez efficace pour leur permettre d'espace supplémentaire. En fait, un morceau d'espace supplémentaire assez grand pour contenir une partie de leur liste partiellement remplie dans une forme non compressée et leur permettre d'effectuer leurs opérations de tri. C'est juste une mauvaise hypothèse.

pour une telle solution, toute personne ayant une connaissance de la façon dont ils font leur compression sera en mesure de concevoir certaines données d'entrée qui ne compriment pas bien pour ce schéma, et la "solution" se cassera très probablement alors en raison de manquer d'espace.

à la place, j'adopte une approche mathématique. Nos sorties possibles sont toutes les listes de longueur len consistant d'éléments dans la gamme 0..MAX. Ici le LEN est de 1.000.000 et notre MAX est de 100.000.000.

pour Len et MAX arbitraires, la quantité de bits nécessaires pour encoder cet état est:

Log2 (MAX Multichoose LEN)

ainsi pour nos nombres, une fois que nous avons terminé la réception et le tri, nous aurons besoin d'au moins Log2 (100.000.000 MC 1.000.000) bits pour stocker notre résultat d'une manière qui peut distinguer de façon unique toutes les sorties possibles.

This is ~= 988ko . Nous avons donc assez d'espace pour conserver notre résultat. De ce point de vue, c'est possible.

[supprimé divagations inutiles maintenant qu'il existe de meilleurs exemples...]

meilleure réponse est ici .

Une autre bonne réponse est ici et utilise essentiellement insertion trier comme la fonction d'étendre la liste par un élément (tampons quelques éléments et pré-tri, pour permettre l'insertion de plus d'un à la fois, économise un peu de temps). utilise un bon encodage d'état compact aussi, seaux de deltas de sept bits

supposons que cette tâche soit possible. Juste avant la sortie, il y aura une représentation en mémoire des millions de nombres assortis. Combien de ces représentations? Puisqu'il peut y avoir des nombres répétés, nous ne pouvons pas utiliser nCr (choisir), mais il y a une opération appelée multichoose qui fonctionne sur multisets .

• Il y a 2.2e2436455 façons de choisir un million de nombres dans la plage de 0..99,999,999.
• qui nécessite 8,093,730 bits pour représenter chaque combinaison possible, ou 1,011,717 octets.

ainsi théoriquement il peut être possible, si vous pouvez venir avec une représentation saine (assez) de la liste triée des nombres. Par exemple, une représentation insensée peut nécessiter une table de recherche de 10 Mo ou des milliers de lignes de code.

cependant, si "1m RAM" signifie un million d'octets, alors clairement il n'y a pas assez d'espace. Le fait que 5% de mémoire en plus le rend théoriquement possible me suggère que la représentation devra être très efficace et probablement pas saine.

(ma réponse originale était fausse, désolé pour le mauvais calcul, voir ci-dessous la pause.)

et ça?

les 27 premiers bits stockent le nombre le plus bas que vous avez vu, puis la différence au nombre suivant vu, encodé comme suit: 5 bits pour stocker le nombre de bits utilisés pour stocker la différence, puis la différence. Utilisez 00000 pour indiquer que vous avez vu ce numéro à nouveau.

Cela fonctionne parce que plus les nombres sont insérée, la différence moyenne entre les nombres diminue, donc vous utilisez moins de bits pour stocker la différence que vous ajoutez plus de nombres. Je crois que cela s'appelle une liste delta.

le pire cas que je puisse penser est tous les nombres uniformément espacés (par 100), par exemple en supposant 0 est le premier nombre:

000000000000000000000000000 00111 1100100
                            ^^^^^^^^^^^^^
                            a million times

27 + 1,000,000 * (5+7) bits = ~ 427k

Reddit à la rescousse!

Si tout ce que vous avait à faire était de les trier, ce problème serait facile. Il faut 122k (1 million de bits) pour stocker les nombres que vous avez vus (0ème bit Sur si 0 a été vu, 2300ème bit Sur si 2300 a été vu, etc.

vous lisez les nombres, les stockez dans le champ de bits, puis décalez les bits tout en gardant un compte.

MAIS, vous devez vous rappeler combien vous l'avez vu. J'ai été inspiré par la réponse de la sous-liste ci-dessus pour trouver ce schéma:

au lieu d'utiliser un bit, utilisez 2 ou 27 bits:

• 00 signifie que vous n'avez pas vu le numéro.
• 01 signifie que vous l'avez vu une fois
• 1 signifie que vous l'avez vu, et les 26 bits sont au nombre de fois.

je pense que cela fonctionne: s'il n'y a pas de doublons, vous avez une liste de 244k. Dans le pire des cas, vous voyez chaque nombre deux fois (si vous voyez un nombre trois fois, il raccourcit le reste de la liste pour vous), ce qui signifie que vous avez vu 50.000 de plus que une fois, et vous avez vu 950.000 items 0 ou 1 fois.

50,000 * 27 + 950,000 * 2 = 396.7 K.

vous pouvez apporter d'autres améliorations si vous utilisez le codage suivant:

0 signifie que vous n'avez pas vu le nombre 10 signifie que vous avez vu une fois 11 est la façon de compter

, ce qui donnera en moyenne 280,7 k de stockage.

EDIT: mes calculs du dimanche matin étaient faux.

Dans le pire des cas, nous voyons 500 000 nombres deux fois, donc les maths deviennent:

500,000 *27 + 500,000 *2 = 1.77 M

l'encodage alternatif résulte en un stockage moyen de

500,000 * 27 + 500,000 = 1.70 M

: (

il y a une solution à ce problème pour toutes les entrées possibles. Tricher.

1. lire les valeurs de m sur TCP, où m est proche du max qui peut être trié en mémoire, peut-être n/4.
2. trier les 250.000 (ou ainsi) nombres et les produire.
3. répéter pour les 3 autres trimestres.
4. permet au récepteur de fusionner les 4 listes de nombres qu'il a reçues pendant qu'il les traite. (Il n'est pas beaucoup plus lent que d'utiliser un liste unique.)

je voudrais essayer une Radix Arbre . Si vous pouviez stocker les données dans un arbre, vous pourriez alors faire une commande de traverse pour transmettre les données.

Je ne suis pas sûr que vous pourriez ajuster ceci en 1MB, mais je pense que cela vaut la peine d'essayer.

Quel genre d'ordinateur utilisez-vous? Il n'a peut-être pas d'autre stockage local "normal", mais a-t-il une RAM Vidéo, par exemple? 1 mégapixel x 32 bits par pixel (say) est assez proche de la taille de votre entrée de données.

(je demande en grande partie à la mémoire de l'ancien Acorn RISC PC , qui pourrait "emprunter" VRAM pour étendre la RAM système disponible, si vous choisissez une faible résolution ou un mode d'écran couleur-profondeur faible!). C'était plutôt utile sur une machine avec seulement quelques Mo de mémoire vive normale.

une représentation d'arbre radix serait proche de traiter ce problème, puisque l'arbre radix profite de la"compression de préfixe". Mais il est difficile de concevoir une représentation d'arbre radix qui pourrait représenter un seul noeud dans un octet -- deux est probablement à propos de la limite.

mais, quelle que soit la façon dont les données sont représentées, une fois qu'elles sont triées, elles peuvent être stockées sous forme comprimée par préfixe, où les nombres 10, 11 et 12 seraient représentés, disons, par 001b, 001b, 001b, indiquant un incrément de 1 par rapport au nombre précédent. Peut-être, alors, 10101b représenterait un accroissement de 5, 1101001b un accroissement de 9, etc.

il y a 10^6 valeurs dans une gamme de 10^8, donc il y a une valeur pour cent points de code en moyenne. Stockez la distance entre le nième point et le (N+1)th. Les valeurs dupliquées ont un saut de 0. Cela signifie que le skip a besoin d'une moyenne d'un peu moins de 7 bits pour stocker, de sorte qu'un million d'entre eux s'adaptera heureusement dans nos 8 millions de bits de stockage.

ces skips doivent être encodés dans un bitstream, disons par Huffman encoding. L'Insertion se fait par itération à travers le flux de bits et réécrire après la nouvelle valeur. Sortie en parcourant et de la rédaction des valeurs implicites. Pour des raisons pratiques, il veut probablement être fait comme, disons, 10^4 listes couvrant 10^4 points de code (et une moyenne de 100 valeurs) chacun.

un bon arbre Huffman pour les données aléatoires peut être construit a priori en supposant une distribution de Poisson (moyenne=variance = 100) Sur la longueur des bennes, mais des statistiques réelles peuvent être maintenues sur l'entrée et utilisées pour générer un arbre optimal pour traiter avec les cas pathologiques.

j'ai un ordinateur avec 1M de RAM et aucun autre stockage local

une autre façon de tricher: vous pourriez utiliser un stockage non local (en réseau) à la place (votre question n'exclut pas cela) et appeler un service en réseau qui pourrait utiliser un simple port de mergesort sur disque (ou juste assez de RAM pour trier en mémoire, puisque vous n'avez besoin d'accepter que des numéros 1M), sans avoir besoin des solutions (certes extrêmement ingénieuses) déjà données.

cela pourrait être de la triche, mais il n'est pas clair si vous êtes à la recherche d'une solution à un problème réel, ou un puzzle qui invite à la flexion des règles... si ce dernier, alors un simple tricheur peut obtenir de meilleurs résultats qu'une solution complexe mais "authentique" (qui, comme d'autres l'ont souligné, ne peut fonctionner que pour des entrées compressibles).

je pense que la solution est de combiner des techniques d'encodage vidéo, à savoir la transformation cosinus discrète. Dans la vidéo numérique, plutôt l'enregistrement de la modification de la luminosité ou de la couleur de la vidéo comme des valeurs régulières telles que 110 112 115 116, chacun est soustrait de la dernière (similaire à l'encodage de longueur d'exécution). 110 112 115 116 devient 110 2 3 1. Les valeurs, 2 3 1 nécessitent moins de bits que les originaux.

alors disons que nous créons une liste des valeurs d'entrée arrivée sur le socket. Nous stockons dans chaque élément, non pas la valeur, mais le décalage de celui qui est devant lui. Nous trions au fur et à mesure, de sorte que les compensations ne seront que positives. Mais le décalage pourrait être de 8 chiffres décimaux de large, ce qui correspond à 3 octets. Chaque élément ne peut pas être de 3 octets, donc nous avons besoin de les emballer. Nous pourrions utiliser le bit supérieur de chaque octet comme un "bit continue", indiquant que le octet suivant fait partie du nombre et les 7 bits inférieurs de chaque octet doivent être combinés. zéro est valable pour les doublons.

comme la liste se remplit, les nombres doivent être rapprochés ensemble, ce qui signifie en moyenne seulement 1 octet est utilisé pour déterminer la distance à la valeur suivante. 7 bits de valeur et 1 bit d'offset si cela vous convient, mais il peut y avoir un sweet spot qui nécessite moins de 8 bits pour une valeur "continue".

J'ai fait une expérience. J'utilise un générateur de nombres aléatoires et je peux ajuster un million de nombres décimaux à 8 chiffres triés dans environ 1279000 octets. Moyen l'espace entre chaque nombre est régulièrement 99...

public class Test {
    public static void main(String[] args) throws IOException {
        // 1 million values
        int[] values = new int[1000000];

        // create random values up to 8 digits lrong
        Random random = new Random();
        for (int x=0;x<values.length;x++) {
            values[x] = random.nextInt(100000000);
        }
        Arrays.sort(values);

        ByteArrayOutputStream baos = new ByteArrayOutputStream();

        int av = 0;    
        writeCompact(baos, values[0]);     // first value
        for (int x=1;x<values.length;x++) {
            int v = values[x] - values[x-1];  // difference
            av += v;
            System.out.println(values[x] + " diff " + v);
            writeCompact(baos, v);
        }

        System.out.println("Average offset " + (av/values.length));
        System.out.println("Fits in " + baos.toByteArray().length);
    }

    public static void writeCompact(OutputStream os, long value) throws IOException {
        do {
            int b = (int) value & 0x7f;
            value = (value & 0x7fffffffffffffffl) >> 7;
            os.write(value == 0 ? b : (b | 0x80));
        } while (value != 0);
    }
}

nous pourrions jouer avec la pile de réseau pour envoyer les numéros dans l'ordre trié avant que nous avons tous les numéros. Si vous envoyez 1M de données, TCP/IP le cassera en paquets de 1500 octets et les diffusera vers la cible. Chaque paquet recevra un numéro de séquence.

on peut le faire à la main. Juste avant de remplir notre mémoire vive, nous pouvons trier ce que nous avons et envoyer la liste à notre cible, mais laisser des trous dans notre séquence autour de chaque nombre. Puis traiter la 2ème 1/2 de la les nombres de la même façon en utilisant ces trous dans la séquence.

la pile de réseau située à l'extrémité du réseau assemblera le flux de données résultant dans l'ordre de séquence avant de le remettre à l'application.

il utilise le réseau pour effectuer un tri de fusion. C'est un piratage total, mais j'ai été inspiré par l'autre piratage de réseau répertorié précédemment.

Google 's (bad), de HN fil. Le style de magasin compte.

votre structure de données initiale est '99999999: 0' (tous les zéros, n'ont pas vu de nombres) et puis disons que vous voyez le nombre 3,866,344 de sorte que votre structure de données devient '3866343: 0,1:1,96133654: 0' comme vous pouvez voir les nombres seront toujours alterner entre le nombre de bits zéro et le nombre de bits '1' de sorte que vous pouvez juste supposer que les nombres impairs représentent 0 bits et le même les numéros 1 bits. Cela devient (3866343,9,96133654)

Leur problème ne semble pas couvrir les doublons, mais disons qu'ils utilisent "0:1" pour les doublons.

Gros problème #1: les insertions de 1M entiers âges .

gros problème #2: comme toutes les solutions d'encodage delta, certaines distributions ne peuvent pas être couvertes de cette façon. Par exemple, des entiers de 1m avec des distances 0: 99 (par exemple + 99 chacun un.) Maintenant, pensez la même chose, mais avec random distance dans la gamme de 0:99 . (Note: 99999999/1000000 = 99,99)

L'approche de Google est à la fois indigne (lente) et incorrecte. Mais pour leur défense, leur problème aurait été légèrement différent.

pour représenter le tableau trié on peut simplement stocker le premier élément et la différence entre les éléments adjacents. De cette façon, nous sommes concernés par l'encodage 10^6 éléments qui peuvent résumer au plus 10^8. Appelons ça D . Pour coder les éléments de D on peut utiliser un code Huffman . Le dictionnaire pour le code de Huffman peut être créé sur la route et le tableau mis à jour chaque fois qu'un nouvel élément est inséré dans le tableau trié (tri d'insertion). Notez que lorsque le dictionnaire change à cause d'un nouvel élément, l'ensemble du tableau doit être mis à jour pour correspondre au nouveau codage.

le nombre moyen de bits pour encoder chaque élément de D est maximisé si nous avons le même nombre de chaque élément unique. Dire éléments d1 , d2 ,..., dN dans D affiche F times. Dans ce cas (dans le pire des cas nous avons à la fois 0 et 10^8 dans la séquence d'entrée) nous avons 151970920"

somme(1<= je <= N ) F . di = 10^8

où

somme(1<= je <= N ) F = 10^6, ou F =10^6/ N et de la fréquence normalisée sera p = F /10^=1/ N

le nombre moyen de bits sera-log2(1/ P ) = log2 ( N ). Dans ces circonstances, nous devrions trouver un cas qui maximise N . Cela se produit si nous avons des nombres consécutifs pour di à partir de 0, ou, di = je -1, donc

10^8= somme (1<= i < = N ) F . di = somme(1<= je <= N ) (10^6/ N ) (je-1) = (10^6/ N ) N ( n -1)/2

c'est à dire

N < = 201. Et pour ce cas le nombre moyen de bits est log2 (201)=7.6511 ce qui signifie que nous aurons besoin d'environ 1 octet par élément d'entrée pour sauvegarder le tableau trié. Notez que cela ne signifie pas D en général ne peut pas avoir plus de 201 éléments. Elle montre juste que si les éléments de D sont distribués uniformément, il ne peut pas ont plus de 201 valeurs uniques.

j'exploiterais le comportement de retransmission de TCP.

1. Rendre le composant TCP créer une grande fenêtre de réception.
2. reçoivent un certain nombre de paquets sans leur envoyer d'ACK.
   • le Processus de ceux en passe de créer certains (préfixe) comprimé structure de données
   • Envoyer en double accusé de réception pour le dernier paquet n'est plus nécessaire/attendre pour la retransmission timeout
   • Goto 2
3. tous les paquets ont été acceptés

cela suppose une sorte de bénéfice de seaux ou de laissez-passer multiples.

probablement en triant les lots / seaux et en les fusionnant. - >arbres radix

utiliser cette technique pour accepter et trier les 80% premiers puis lire les 20% derniers, vérifier que les 20% derniers ne contiennent pas des nombres qui se poseraient dans les 20% premiers des nombres les plus bas. Puis envoyer les 20% plus bas numéros, Supprimer de mémoire, accepter les 20% restants de nouveaux numéros et fusionner.**

si le flux d'entrée pouvait être reçu quelques fois ce serait beaucoup plus facile (aucune information à ce sujet, l'idée et le temps-Problème de performance).

alors, nous pourrions compter les valeurs décimales. Avec les valeurs comptées, il serait facile de faire le flux de sortie. Compresser en comptant les valeurs. Il dépend de ce que serait dans le flux d'entrée.

si le flux d'entrée pouvait être reçu plusieurs fois ce serait beaucoup plus facile (pas d'information à ce sujet, l'idée et le temps-Problème de performance). Ensuite, nous pourrions compter les valeurs décimales. Avec les valeurs comptées, il serait facile de rendre le flux de sortie. Compresser en comptant les valeurs. Cela dépend de ce que serait dans le flux d'entrée.

est un problème secondaire. Comme d'autres l'ont dit, simplement stocker les entiers est difficile, et ne peut pas travailler sur toutes les entrées , car 27 bits par nombre serait nécessaire.

mon point de vue sur ceci est: stocker seulement les différences entre les entiers consécutifs (triés), car ils seront très probablement petits. Ensuite, utilisez un schéma de compression, par exemple avec 2 bits supplémentaires par nombre d'entrée, pour coder combien de bits le nombre est stocké. Quelque chose comme:

00 -> 5 bits
01 -> 11 bits
10 -> 19 bits
11 -> 27 bits

il devrait être possible de stocker un nombre suffisant de listes d'entrées possibles à l'intérieur de la contrainte mémoire donnée. Les maths de la façon de choisir le schéma de compression pour qu'il fonctionne sur le nombre maximum d'entrées, sont au-delà de moi.

j'espère que vous serez en mesure d'exploiter domaine-connaissances spécifiques de votre entrée pour trouver un assez bon système de compression integer basé sur cela.

Oh et puis, vous faites un tri d'insertion sur cette liste triée que vous recevez des données.

vise maintenant à une solution réelle, couvrant tous les cas possibles d'entrée dans la gamme de 8 chiffres avec seulement 1MB de RAM. NOTE: les travaux en cours se poursuivront demain. En utilisant le codage arithmétique des deltas des ints triés, le pire des cas pour 1M des ints triés coûterait environ 7bits par entrée (depuis 99999999/1000000 est 99, et log2(99) est presque 7 bits).

mais vous avez besoin des entiers 1m triés pour obtenir 7 ou 8 bits! Des séries plus courtes auraient des deltas plus grands, donc plus bits par élément.

je travaille à en prendre le plus possible et à comprimer (presque) sur place. Le premier lot de près de 250K ints aurait besoin d'environ 9 bits chacun au mieux. Donc le résultat devrait prendre environ 275KB. Répétez plusieurs fois avec le reste de la mémoire libre. Puis décompressez-fusionner-en-place-compresser ces morceaux compressés. C'est assez dur , mais possible. Je pense que.

les listes fusionnées se rapprocheraient de plus en plus des 7 entier cible. Mais je ne sais pas combien d'itérations il faudrait de la boucle de fusion. Peut-être 3.

mais l'imprécision de la mise en œuvre du codage arithmétique pourrait rendre cela impossible. Si ce problème est possible, il serait extrêmement serré.

des volontaires?

vous avez juste besoin de stocker les différences entre les numéros dans la séquence, et d'utiliser un encodage pour compresser ces numéros de séquence. Nous avons 2^23 bits. Nous le diviserons en morceaux de 6bits, et laisserons Le Dernier bit indiquer si le nombre s'étend à 6 autres bits (5bits plus morceau extensible).

ainsi, 000010 est 1, et 000100 est 2. 000001100000 c'est 128. Maintenant, nous considérons le pire cast en représentant des différences dans la séquence d'un nombre allant jusqu'à 10 000 000. Y les différences supérieures à 2^5, 10.000.000/2^10 les différences supérieures à 2^10, et 10.000.000/2^15 les différences supérieures à 2^15, etc.

ainsi, nous ajoutons combien de bits il faudra pour représenter notre séquence. Nous avons 1.000.000*6 + roundup(10,000,000/2^5)*6+roundup(10,000,000/2^10)*6+roundup(10,000,000/2^15)*6+roundup(10,000,000/2^20)*4=7935479.

2^24 = 8388608. Depuis 8388608 > 7935479, nous devrions facilement avoir assez de mémoire. Nous aurez probablement besoin d'un peu de mémoire pour stocker la somme de où sont quand nous insérer de nouveaux numéros. Nous passons ensuite à travers la séquence, et trouver où insérer notre nouveau numéro, diminuer la différence suivante si nécessaire, et tout déplacer après elle droite.

si nous ne savons rien de ces nombres, nous sommes limités par les contraintes suivantes:

• nous avons besoin de charger tous les numéros avant de pouvoir les trier,
• l'ensemble des nombres n'est pas compressible.

si ces hypothèses sont valables, il n'y a aucun moyen d'effectuer votre tâche, car vous aurez besoin d'au moins 26.575.425 bits de stockage (3.321.929 octets).

Que pouvez-vous nous dire à propos de vos données ?

le truc est de représenter l'état des algorithmes, qui est un multi-set entier, comme un flux comprimé de" increment counter"="+ "et"output counter"="!" caractère. Par exemple, l'ensemble {0,3,3,4} serait représenté comme "!+++!!+!", suivi par un certain nombre de "+" caractères. Pour modifier le multi-set vous diffusez les caractères, en gardant seulement un montant constant décompressé à la fois, et faire des changements inplace avant de les diffuser à nouveau sous forme comprimée.

détails

nous savons qu'il y a exactement 10^6 nombres dans le jeu final, donc il y a tout au plus 10^6 "!" caractère. Nous savons aussi que notre gamme de taille a 10^8, ce qui signifie qu'au plus 10^8 "+" caractères. Le nombre de façons dont nous pouvons organiser 10^6 "!"s parmi 10 ^ 8" + "s est (10^8 + 10^6) choose 10^6 , et donc en spécifiant un arrangement particulier prend ~0.965 MiB ` de données. Ce sera un ajustement serré.

Nous pouvons traiter chaque caractère indépendant sans dépasser notre quota. Il y a exactement 100 fois plus de "+" caractères de "!"caractères, ce qui simplifie à 100:1 chances de chaque caractère étant un "+" si nous oublions qu'ils sont dépendants. Odds of 100: 101 correspond à ~0.08 bits par caractère , pour un total presque identique de ~0.965 MiB (ignorer la dépendance a un coût de seulement ~12 bits dans ce cas!).

la technique la plus simple pour stocker des caractères indépendants avec une probabilité préalable connue est codage Huffman . Notez que nous avons besoin d'un arbre d'une taille irréalisable (un arbre huffman pour des blocs de 10 caractères a un coût moyen par bloc d'environ 2,4 bits, pour un total de ~2,9 Mib. Un arbre huffman pour des blocs de 20 caractères a un coût moyen par bloc d'environ 3 bits, ce qui est un total de ~1,8 MiB. Nous allons sans doute avoir besoin d'un bloc de taille de l'ordre d'un cent, ce qui implique plus de noeuds dans notre arbre que tout l'équipement informatique qui a jamais existé peut stocker.). Cependant, ROM est techniquement "libre" selon le problème et les solutions pratiques qui tirent profit de la régularité dans l'arbre sera essentiellement le même.

Pseudo-code

• suffisamment grand arbre de huffman (ou similaire par bloc de compression de données) stockés dans la mémoire ROM
• commence par une chaîne compressée de 10^8 "+" caractères.
• pour insérer le nombre N, filtrer la chaîne compressée jusqu'à ce que les caractères N " + "soient passés puis insérer un"!". Streamer la chaîne recompressée sur la précédente comme vous allez, en gardant une quantité constante de blocs tamponnés pour éviter les dépassements / sous-passes.
• répéter un million de fois: [input, stream decompress>insert>compress], puis décompresser en sortie

nous avons 1 MB - 3 KB RAM = 2^23 - 3*2^13 bits = 8388608-24576 = 8364032 bits disponibles.

nous sommes donnés 10^6 nombres dans une gamme de 10^8. Cela donne un écart moyen de ~100 < 2^7 = 128

considérons d'abord le problème plus simple des nombres relativement uniformément espacés quand tous les écarts sont < 128. Cela est facile. Il suffit de stocker le premier numéro et les 7-bits lacunes:

(27 bits) + 10^6 nombres d'intervalle de 7 bits = 7000027 bits requis

Note les nombres répétés ont des écarts de 0.

mais que se passe-t-il si nous avons des trous plus grands que 127?

OK, disons qu'une taille d'espacement < 127 est représentée directement, mais une taille d'espacement de 127 est suivie d'un encodage continu à 8 bits pour la longueur d'espacement réelle:

 10xxxxxx xxxxxxxx                       = 127 .. 16,383
 110xxxxx xxxxxxxx xxxxxxxx              = 16384 .. 2,097,151

etc.

notez que cette représentation de nombre décrit sa propre longueur de sorte que nous savons quand le prochain numéro d'écart commence.

avec seulement de petites lacunes < 127, cela nécessite encore 7000027 bits.

il peut y avoir jusqu'à (10^8)/(2^7) = 781250 23-Nombre de bits, nécessitant un supplément de 16*781.250 = 12.500.000 bits, ce qui est trop. Nous avons besoin d'une représentation plus compacte et lentement croissante des écarts.

la taille moyenne de l'écart est de 100 donc si nous les réorganisons comme [100, 99, 101, 98, 102, ..., 2, 198, 1, 199, 0, 200, 201, 202, ...] et l'indexer avec une base de Fibonacci binaire dense encodage sans zéros (par exemple, 11011=8+5+2+1=16) avec des nombres délimités par '00', Je pense que nous pouvons garder la représentation de l'écart assez courte, mais il a besoin de plus d'analyse.

tout en recevant le flux faire ces étapes.

1ère série raisonnables taille de bloc

Pseudo-Code idée:

1. La première étape serait de trouver tous les doublons et de les coller dans un dictionnaire avec son compte et de les supprimer.
2. la troisième étape serait de placer le nombre qui existe dans l'ordre de leurs étapes algorithmiques et de les placer dans les compteurs dictionnaires spéciaux avec le premier numéro et leur pas comme n, n+1 ... ,n+2, 2n, 2n+1, 2n+2...
3. commencer à compresser en morceaux quelques gammes raisonnables de nombre comme chaque 1000 ou jamais 10000 les nombres restants qui semblent moins souvent à répéter.
4. décompresser cette plage si un nombre est trouvé et l'ajouter à la plage et le laisser non compressé pendant un certain temps plus longtemps.
5. sinon il suffit d'ajouter ce nombre à un byte [chunkSize]

Continuez les 4 premières étapes tout en recevant le flux. La dernière étape serait soit d'échouer si vous avez dépassé la mémoire ou de commencer à outputing le résultat une fois que toutes les données sont collectées en commençant à trier les plages et recracher les résultats dans l'ordre et de décompresser ceux qui ont besoin d'être non compressé et les trier lorsque vous arrivez à eux.

ceci suppose la base 10 et comme exemple, votre mémoire utilise des mots de 8 bits: Mémoire cartographier la gamme entière des nombres en utilisant des incréments de 3 bits. Les 3 premiers bits correspondraient au nombre 0. Le deuxième ensemble de 3 bits correspondrait au nombre 1. 300 millièmes série de 3-bit serait la carte au numéro 300k. Répétez ceci jusqu'à ce que vous ayez tracé tous les numéros à 8 chiffres. Cela totaliserait 375k octets au total si la plage de mémoire était continue.

Le 1er peu des 3 marquerait la présence du nombre. Les 2 bits suivants indiqueraient la quantité de doublons qui pourraient être représentés en octets(1..3) si aucun, le champ des doublons sera 00. Il y aura une deuxième liste qui utilise un compteur qui augmente chaque fois qu'un champ de 3 bits est marqué comme ayant un duplicata. S'il est marqué avec 1, il aura une plage de bits unique pour compter la quantité de doublons qu'il a. 8 bits peut représenter une plage 255.

comme je perds la notion des pensées. La deuxième liste tiendra compte du nombre de doublons pour chaque numéro. si le 255e numéro a un duplicata et est le premier à avoir un duplicata, son index dans la liste sera 0. Si 23,543 est le deuxième nombre à avoir un double de son index sera 1. Se laver,se lever et se répéter.

dans le pire des cas, vous avez des numéros de 500k avec des doubles. Ceci peut être représenté par un octet(depuis le 1er s'inscrit dans facile). Donc 375kB (idéalement) + 500KB bytes est proche .875MO. Selon votre processeur cela devrait laisser assez de place pour les pointeurs, l'indexation et tous les autres trucs amusants.

si vous avez un numéro unique qui a 1m doubles. tous vous avez besoin est de 3 octets, puisque limitée à 1M numéros, c'est tout ce que vous avez à vous soucier. Donc, sur votre deuxième liste, il sera juste 3 exemptions du montant total.

maintenant pour la partie amusante. La deuxième liste devront être triés pour chaque nouveau numéro. Dans le champ 3 bits les 2 dernières sont le nombre d'octets que contient le nombre de doublons. Étant donné que la deuxième liste devrait être en ordre, elle devra être triée. Puisque la quantité d'octets peut varier. Pensez insertion tri!

cela garderait la quantité de pointeurs et de choses que vous devez augmenter au minimum de sorte que vous devriez avoir un peu de flexibilité avec les octets peut-être 250k laissés.

GoodLuck! Cela semble tellement plus élégant dans mon esprit...