Trier les coordonnées de latitude et de longitude en quadrilatère ordonné dans le sens horaire

Compte tenu des points:

   4  +        [d]            [g]                 
      |                             
   3 [a]            [e]                 
      |                             
   2  +                  [f]       [h]    
      |                             
   1  +   [b]                             
      |                             
   0  +----+---[c]---+----+----+----+
      0    1    2    3    4    5    6

Vous voulez trouver la marche liée suivante:

   4  +     ___[d]------------[g]                 
      |  __/                     \    
   3 [a]/           [e]__         \       
      | \             \_ ```---    \  
   2  +  \              `[f]   \___[h]    
      |   \           __/            
   1  +   [b]      __/                   
      |      \    /                
   0  +----+--`[c]---+----+----+----+
      0    1    2    3    4    5    6

?

Si c'est correct, voici un moyen:

• trouver la plus haute point, P_haut, dans l'ensemble des points. En cas d'égalité, choisissez le point avec la plus petite coordonnée x
• trier tous les points en comparant les pentes m_{, je} et m_j les lignes de chaque paire de points (à l'exclusion de P_haut!) P_{, je} et P_j faire quand passant par P_haut
  • si m_{, je} et m_j sont égaux, de laisser le point P_{, je} ou P_j le plus proche de P_haut arrivé, premier
  • si m_{, je} est positif et m_j est négatif (ou nul), P_j vient en premier
  • si M _i et m _j sont tous deux positifs ou négatifs, laissez le point appartenant à la ligne avec la plus grande pente venir en premier

Voici une démo rapide pour la carte:

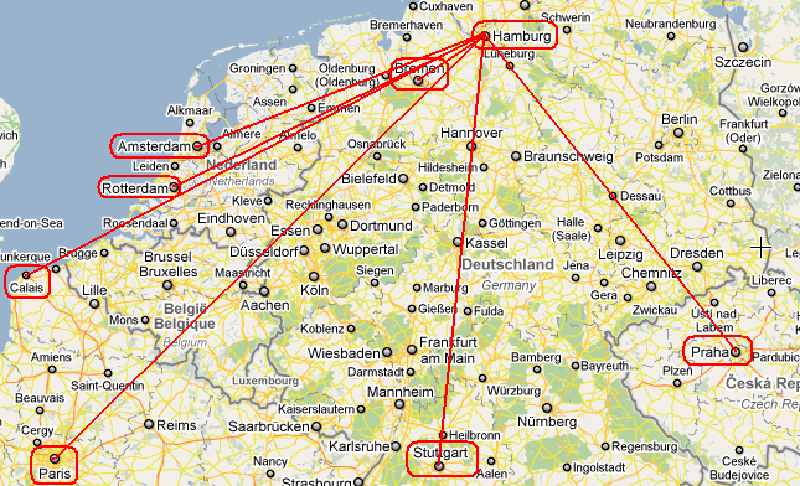
(je connais peu de JavaScript, donc je pourrais, ou probablement avoir violé certaines conventions de code JavaScript...):

var points = [
    new Point("Stuttgard", 48.7771056, 9.1807688),
    new Point("Rotterdam", 51.9226899, 4.4707867),
    new Point("Paris", 48.8566667, 2.3509871),
    new Point("Hamburg", 53.5538148, 9.9915752),
    new Point("Praha", 50.0878114, 14.4204598),
    new Point("Amsterdam", 52.3738007, 4.8909347),
    new Point("Bremen", 53.074981, 8.807081),
    new Point("Calais", 50.9580293, 1.8524129),
];
var upper = upperLeft(points);

print("points :: " + points);
print("upper  :: " + upper);
points.sort(pointSort);
print("sorted :: " + points);

// A representation of a 2D Point.
function Point(label, lat, lon) {

    this.label = label;
    this.x = (lon + 180) * 360;
    this.y = (lat + 90) * 180;

    this.distance=function(that) {
        var dX = that.x - this.x;
        var dY = that.y - this.y;
        return Math.sqrt((dX*dX) + (dY*dY));
    }

    this.slope=function(that) {
        var dX = that.x - this.x;
        var dY = that.y - this.y;
        return dY / dX;
    }

    this.toString=function() {
        return this.label;
    }
}

// A custom sort function that sorts p1 and p2 based on their slope
// that is formed from the upper most point from the array of points.
function pointSort(p1, p2) {
    // Exclude the 'upper' point from the sort (which should come first).
    if(p1 == upper) return -1;
    if(p2 == upper) return 1;

    // Find the slopes of 'p1' and 'p2' when a line is 
    // drawn from those points through the 'upper' point.
    var m1 = upper.slope(p1);
    var m2 = upper.slope(p2);

    // 'p1' and 'p2' are on the same line towards 'upper'.
    if(m1 == m2) {
        // The point closest to 'upper' will come first.
        return p1.distance(upper) < p2.distance(upper) ? -1 : 1;
    }

    // If 'p1' is to the right of 'upper' and 'p2' is the the left.
    if(m1 <= 0 && m2 > 0) return -1;

    // If 'p1' is to the left of 'upper' and 'p2' is the the right.
    if(m1 > 0 && m2 <= 0) return 1;

    // It seems that both slopes are either positive, or negative.
    return m1 > m2 ? -1 : 1;
}

// Find the upper most point. In case of a tie, get the left most point.
function upperLeft(points) {
    var top = points[0];
    for(var i = 1; i < points.length; i++) {
        var temp = points[i];
        if(temp.y > top.y || (temp.y == top.y && temp.x < top.x)) {
            top = temp;
        }
    }
    return top;
}

Note: vous devriez doubler, ou tripler vérifier les conversions de lat,lon à x,y car je suis un novice s'il s'agit de SIG!!! Mais peut-être que vous n'avez même pas besoin de convertir quoi que ce soit. Si vous ne le faites pas, la fonction upperLeft peut simplement renvoyer le point le plus bas au lieu du point le plus élevé, en fonction de l'emplacement des points en question. Encore: triple vérifiez ces hypothèses!

Lorsque exécute l'extrait ci-dessus , ce qui suit est imprimé:

points :: Stuttgard,Rotterdam,Paris,Hamburg,Praha,Amsterdam,Bremen,Calais
upper  :: Hamburg
sorted :: Hamburg,Praha,Stuttgard,Paris,Bremen,Calais,Rotterdam,Amsterdam

Fonction De Distance Alternative

function distance(lat1, lng1, lat2, lng2) {
  var R = 6371; // km
  var dLat = (lat2-lat1).toRad();
  var dLon = (lng2-lng1).toRad();
  var a = Math.sin(dLat/2) * Math.sin(dLat/2) +
          Math.cos(lat1.toRad()) * Math.cos(lat2.toRad()) *
          Math.sin(dLon/2) * Math.sin(dLon/2);
  var c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
  return R * c;
}