Résoudre le problème NP-complete dans XKCD
du problème/de La bande dessinée en question: http://xkcd.com/287/
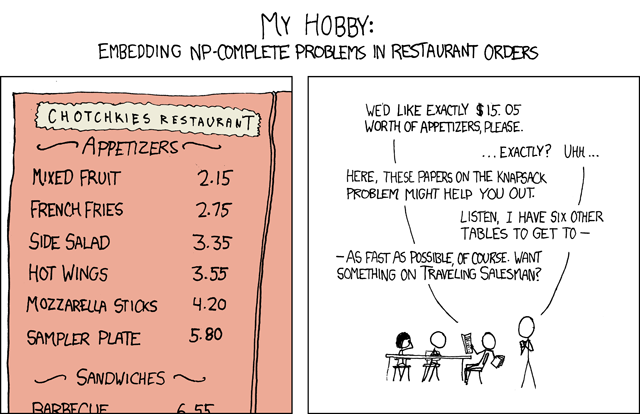
je ne suis pas sûr que c'est la meilleure façon de le faire, mais voici ce que j'ai trouvé jusqu'à présent. J'utilise CFML, mais ça devrait être lisible par n'importe qui.
<cffunction name="testCombo" returntype="boolean">
<cfargument name="currentCombo" type="string" required="true" />
<cfargument name="currentTotal" type="numeric" required="true" />
<cfargument name="apps" type="array" required="true" />
<cfset var a = 0 />
<cfset var found = false />
<cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
<cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />
<cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />
<cfif arguments.currentTotal eq 15.05>
<!--- print current combo --->
<cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />
<cfreturn true />
<cfelseif arguments.currentTotal gt 15.05>
<cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />
<cfreturn false />
<cfelse>
<!--- less than 15.05 --->
<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />
<cfset found = testCombo(arguments.currentCombo, arguments.currentTotal, arguments.apps) />
</cfif>
</cfloop>
</cffunction>
<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />
<cfloop from="1" to="6" index="b">
<cfoutput>#testCombo(apps[b].name, apps[b].cost, apps)#</cfoutput>
</cfloop>
le code ci-dessus me dit que la seule combinaison qui s'élève à $ 15.05 est 7 commandes de fruits mélangés, et il faut 232 exécutions de mon fonction testCombo à remplir.
y a-t-il un meilleur algorithme pour trouver la bonne solution? Ai-je venir à la bonne solution?
15 réponses
le point à propos d'un NP-problème complet n'est pas qu'il est délicat sur un petit ensemble de données, mais que la quantité de travail pour le résoudre augmente à une vitesse supérieure à polynomial, i.e. il n'y a pas d'algorithme O(N^x).
Si l'heure de la complexité est O(n!), comme dans (je crois) les deux problèmes mentionnés ci-dessus, qui est dans NP.
il donne toutes les permutations des solutions, mais je pense que je bats tout le monde pour la taille du code.
item(X) :- member(X,[215, 275, 335, 355, 420, 580]).
solution([X|Y], Z) :- item(X), plus(S, X, Z), Z >= 0, solution(Y, S).
solution([], 0).
Solution avec swiprolog:
?- solution(X, 1505).
X = [215, 215, 215, 215, 215, 215, 215] ;
X = [215, 355, 355, 580] ;
X = [215, 355, 580, 355] ;
X = [215, 580, 355, 355] ;
X = [355, 215, 355, 580] ;
X = [355, 215, 580, 355] ;
X = [355, 355, 215, 580] ;
X = [355, 355, 580, 215] ;
X = [355, 580, 215, 355] ;
X = [355, 580, 355, 215] ;
X = [580, 215, 355, 355] ;
X = [580, 355, 215, 355] ;
X = [580, 355, 355, 215] ;
No
N'est-il pas plus élégant avec la récursion (en Perl)?
#!/usr/bin/perl
use strict;
use warnings;
my @weights = (2.15, 2.75, 3.35, 3.55, 4.20, 5.80);
my $total = 0;
my @order = ();
iterate($total, @order);
sub iterate
{
my ($total, @order) = @_;
foreach my $w (@weights)
{
if ($total+$w == 15.05)
{
print join (', ', (@order, $w)), "\n";
}
if ($total+$w < 15.05)
{
iterate($total+$w, (@order, $w));
}
}
}
sortie
marco@unimatrix-01:~$ ./xkcd-knapsack.pl
2.15, 2.15, 2.15, 2.15, 2.15, 2.15, 2.15
2.15, 3.55, 3.55, 5.8
2.15, 3.55, 5.8, 3.55
2.15, 5.8, 3.55, 3.55
3.55, 2.15, 3.55, 5.8
3.55, 2.15, 5.8, 3.55
3.55, 3.55, 2.15, 5.8
3.55, 5.8, 2.15, 3.55
5.8, 2.15, 3.55, 3.55
5.8, 3.55, 2.15, 3.55
même si knapsack est NP complet, c'est un problème très spécial: le programme dynamique habituel pour lui est en fait excellent ( http://en.wikipedia.org/wiki/Knapsack_problem )
et si vous faites la bonne analyse, il s'avère que C'est O(nW), n étant le nombre d'articles, et W étant le nombre cible. Le problème est quand vous devez DP sur un grand W, c'est quand nous obtenons le comportement NP. Mais pour la plupart, knapsack est assez bien sage et vous pouvez résoudre vraiment grandes instances de sans problèmes. En ce qui concerne les problèmes NP complets vont, knapsack est l'un des plus faciles.
Voici la solution en utilisant constraint.py
>>> from constraint import *
>>> problem = Problem()
>>> menu = {'mixed-fruit': 2.15,
... 'french-fries': 2.75,
... 'side-salad': 3.35,
... 'hot-wings': 3.55,
... 'mozarella-sticks': 4.20,
... 'sampler-plate': 5.80}
>>> for appetizer in menu:
... problem.addVariable( appetizer, [ menu[appetizer] * i for i in range( 8 )] )
>>> problem.addConstraint(ExactSumConstraint(15.05))
>>> problem.getSolutions()
[{'side-salad': 0.0, 'french-fries': 0.0, 'sampler-plate': 5.7999999999999998, 'mixed-fruit': 2.1499999999999999, 'mozarella-sticks': 0.0, 'hot-wings': 7.0999999999999996},
{'side-salad': 0.0, 'french-fries': 0.0, 'sampler-plate': 0.0, 'mixed-fruit': 15.049999999999999, 'mozarella-sticks': 0.0, 'hot-wings': 0.0}]
ainsi la solution est de commander une assiette de sampler, un fruit mélangé, et 2 ordres des ailes chaudes, ou commander 7 fruits mélangés.
Voici une solution avec F#:
#light
type Appetizer = { name : string; cost : int }
let menu = [
{name="fruit"; cost=215}
{name="fries"; cost=275}
{name="salad"; cost=335}
{name="wings"; cost=355}
{name="moz sticks"; cost=420}
{name="sampler"; cost=580}
]
// Choose: list<Appetizer> -> list<Appetizer> -> int -> list<list<Appetizer>>
let rec Choose allowedMenu pickedSoFar remainingMoney =
if remainingMoney = 0 then
// solved it, return this solution
[ pickedSoFar ]
else
// there's more to spend
[match allowedMenu with
| [] -> yield! [] // no more items to choose, no solutions this branch
| item :: rest ->
if item.cost <= remainingMoney then
// if first allowed is within budget, pick it and recurse
yield! Choose allowedMenu (item :: pickedSoFar) (remainingMoney - item.cost)
// regardless, also skip ever picking more of that first item and recurse
yield! Choose rest pickedSoFar remainingMoney]
let solutions = Choose menu [] 1505
printfn "%d solutions:" solutions.Length
solutions |> List.iter (fun solution ->
solution |> List.iter (fun item -> printf "%s, " item.name)
printfn ""
)
(*
2 solutions:
fruit, fruit, fruit, fruit, fruit, fruit, fruit,
sampler, wings, wings, fruit,
*)
vous avez toutes les combinaisons correctes maintenant, mais vous vérifiez encore beaucoup plus que vous avez besoin de (comme en témoignent les nombreuses permutations votre résultat montre). De plus, vous omettez le dernier article qui atteint la note de 15.05.
j'ai une version PHP qui fait 209 itérations de l'appel récursif (il fait 2012 si j'obtiens toutes les permutations). Vous pouvez réduire votre compte si juste avant la fin de votre boucle, vous tirez sur l'élément que vous venez de vérifier.
Je ne connais pas la syntaxe de CF, mais ce sera quelque chose comme ceci:
<cfelse>
<!--- less than 15.50 --->
<!--<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />-->
<cfset found = testCombo(CC, CT, arguments.apps) />
------- remove the item from the apps array that was just checked here ------
</cfif>
</cfloop>
EDIT: Pour référence, voici ma version de PHP:
<?
function rc($total, $string, $m) {
global $c;
$m2 = $m;
$c++;
foreach($m as $i=>$p) {
if ($total-$p == 0) {
print "$string $i\n";
return;
}
if ($total-$p > 0) {
rc($total-$p, $string . " " . $i, $m2);
}
unset($m2[$i]);
}
}
$c = 0;
$m = array("mf"=>215, "ff"=>275, "ss"=>335, "hw"=>355, "ms"=>420, "sp"=>580);
rc(1505, "", $m);
print $c;
?>
sortie
mf mf mf mf mf mf mf
mf hw hw sp
209
EDIT 2:
puisqu'expliquer pourquoi vous pouvez supprimer les éléments prendra un peu plus que je ne pourrais rentrer dans un commentaire, je l'ajoute ici.
En Gros, chaque récursion trouvera toutes les combinaisons qui inclure l'élément de recherche actuel (p. ex., la première étape permettra de tout trouver, y compris au moins un fruit mélangé). La meilleure façon de le comprendre est de tracer l'exécution, mais depuis que va prendre beaucoup d'espace, je vais le faire comme si la cible était 6.45.
MF (2.15)
MF (4.30)
MF (6.45) *
FF (7.05) X
SS (7.65) X
...
[MF removed for depth 2]
FF (4.90)
[checking MF now would be redundant since we checked MF/MF/FF previously]
FF (7.65) X
...
[FF removed for depth 2]
SS (5.50)
...
[MF removed for depth 1]
à ce stade, nous avons vérifié chaque combinaison qui comprend un fruit mélangé, il n'est donc pas nécessaire de vérifier les fruits mélangés à nouveau. Vous pouvez utiliser la même logique pour tailler le tableau à chacune des profondeurs récurrences.
tracer à travers elle comme ceci a réellement suggéré un autre léger gain de temps -- sachant que les prix sont triés de bas en haut signifie que nous n'avons pas besoin de continuer à vérifier les articles une fois que nous allons au-dessus de la cible.
je voudrais faire une suggestion au sujet de la conception de l'algorithme lui-même (qui est comment j'ai interprété l'intention de votre question originale). Voici un fragment de la solution j'ai écrit:
....
private void findAndReportSolutions(
int target, // goal to be achieved
int balance, // amount of goal remaining
int index // menu item to try next
) {
++calls;
if (balance == 0) {
reportSolution(target);
return; // no addition to perfect order is possible
}
if (index == items.length) {
++falls;
return; // ran out of menu items without finding solution
}
final int price = items[index].price;
if (balance < price) {
return; // all remaining items cost too much
}
int maxCount = balance / price; // max uses for this item
for (int n = maxCount; 0 <= n; --n) { // loop for this item, recur for others
++loops;
counts[index] = n;
findAndReportSolutions(
target, balance - n * price, index + 1
);
}
}
public void reportSolutionsFor(int target) {
counts = new int[items.length];
calls = loops = falls = 0;
findAndReportSolutions(target, target, 0);
ps.printf("%d calls, %d loops, %d falls%n", calls, loops, falls);
}
public static void main(String[] args) {
MenuItem[] items = {
new MenuItem("mixed fruit", 215),
new MenuItem("french fries", 275),
new MenuItem("side salad", 335),
new MenuItem("hot wings", 355),
new MenuItem("mozzarella sticks", 420),
new MenuItem("sampler plate", 580),
};
Solver solver = new Solver(items);
solver.reportSolutionsFor(1505);
}
...
(notez que le constructeur fait trier les éléments de menu en augmentant le prix, pour permettre la terminaison anticipée en temps constant lorsque le solde restant est plus petit que n'importe quel élément de menu restant.)
la sortie d'un échantillon est:
7 mixed fruit (1505) = 1505
1 mixed fruit (215) + 2 hot wings (710) + 1 sampler plate (580) = 1505
348 calls, 347 loops, 79 falls
la suggestion de conception que je veux souligner est que dans le code ci-dessus, chaque appel imbriqué (récursif) de findAndReportSolution(...) traite de la quantité d'exactement un élément de menu, identifié par l'argument index . En d'autres termes, le nichage récursif suit le comportement d'un ensemble en ligne de boucles imbriquées; l'Extérieur compte les utilisations possibles du premier élément de menu, le suivant compte les utilisations du second menu item, etc. (Sauf, bien sûr, l'utilisation de la récursion libère le code de la dépendance d'un nombre spécifique d'éléments de menu!)
je suggère que cela facilite la conception du code, et facilite la compréhension de ce que fait chaque invocation (en tenant compte de toutes les utilisations possibles d'un élément spécifique, en déléguant le reste du menu aux appels subordonnés). Il évite également l'explosion combinatoire de produire tous les arrangements d'une solution à plusieurs éléments (comme dans la seconde ligne de la sortie ci-dessus, qui ne se produit qu'une fois, au lieu de plusieurs fois avec des ordres différents des articles).
j'essaie d'optimiser l ' "évidence" du code, plutôt que d'essayer de minimiser le nombre d'appels d'une méthode spécifique. Par exemple, la conception ci-dessus permet à un appel délégué de déterminer si une solution a été atteinte, plutôt que d'envelopper cette vérification autour du point de l'appel, ce qui réduirait le nombre d'appels au détriment de l'encombrement code.
Hmm, tu sais ce qui est bizarre. La solution est sept du premier article sur le menu.
puisque cela devait évidemment être résolu par le papier et le crayon dans un court laps de temps, pourquoi ne pas diviser le total de l'ordre par le prix de chaque article pour voir si par hasard ils ont commandé des multiples d'un article?
par exemple,
15.05/2.15 = 7 fruits mélangés 15.05/2.75 = 5.5 frites.
et puis passer à autre chose pour des combinaisons simples...
15 / (2.15 + 2.75) = 3.06122449 mélange de fruits avec des frites.
en d'autres termes, supposer que la solution est censée être simple et soluble par un humain sans accès à un ordinateur. Tester ensuite si la (les) solution(s) la(les) plus simple (s), la (les) plus évidente (s) (et donc cachée (s) à la vue de tous) fonctionne (s).
je jure que je tire ceci au coney local ce week-end quand je commande 4,77 $ d'entrées (y compris taxes) à 4h30 après la fermeture du club.
en python.
J'ai eu quelques problèmes avec "global vars" donc j'ai mis la fonction comme méthode d'un objet. Il est récursif et il s'appelle 29 fois pour la question dans la bande dessinée, s'arrêtant au premier match réussi
class Solver(object):
def __init__(self):
self.solved = False
self.total = 0
def solve(s, p, pl, curList = []):
poss = [i for i in sorted(pl, reverse = True) if i <= p]
if len(poss) == 0 or s.solved:
s.total += 1
return curList
if abs(poss[0]-p) < 0.00001:
s.solved = True # Solved it!!!
s.total += 1
return curList + [poss[0]]
ml,md = [], 10**8
for j in [s.solve(p-i, pl, [i]) for i in poss]:
if abs(sum(j)-p)<md: ml,md = j, abs(sum(j)-p)
s.total += 1
return ml + curList
priceList = [5.8, 4.2, 3.55, 3.35, 2.75, 2.15]
appetizers = ['Sampler Plate', 'Mozzarella Sticks', \
'Hot wings', 'Side salad', 'French Fries', 'Mixed Fruit']
menu = zip(priceList, appetizers)
sol = Solver()
q = sol.solve(15.05, priceList)
print 'Total time it runned: ', sol.total
print '-'*30
order = [(m, q.count(m[0])) for m in menu if m[0] in q]
for o in order:
print '%d x %s \t\t\t (%.2f)' % (o[1],o[0][1],o[0][0])
print '-'*30
ts = 'Total: %.2f' % sum(q)
print ' '*(30-len(ts)-1),ts
sortie:
Total time it runned: 29
------------------------------
1 x Sampler Plate (5.80)
2 x Hot wings (3.55)
1 x Mixed Fruit (2.15)
------------------------------
Total: 15.05
en fait, j'ai encore remanié mon algorithme. Il y avait plusieurs combinaisons correctes que je manquais, et c'était dû au fait que je revenais dès que le coût dépassait 15.05 -- Je ne me souciais pas de vérifier d'autres articles (moins chers) que je pouvais ajouter. Voici mon nouvel algorithme:
<cffunction name="testCombo" returntype="numeric">
<cfargument name="currentCombo" type="string" required="true" />
<cfargument name="currentTotal" type="numeric" required="true" />
<cfargument name="apps" type="array" required="true" />
<cfset var a = 0 />
<cfset var found = false />
<cfset var CC = "" />
<cfset var CT = 0 />
<cfset tries = tries + 1 />
<cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
<cfset combos = combos + 1 />
<cfset CC = listAppend(arguments.currentCombo, arguments.apps[a].name) />
<cfset CT = arguments.currentTotal + arguments.apps[a].cost />
<cfif CT eq 15.05>
<!--- print current combo --->
<cfoutput><strong>#CC# = 15.05</strong></cfoutput><br />
<cfreturn true />
<cfelseif CT gt 15.05>
<!--<cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />-->
<cfelse>
<!--- less than 15.50 --->
<!--<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />-->
<cfset found = testCombo(CC, CT, arguments.apps) />
</cfif>
</cfloop>
<cfreturn found />
</cffunction>
<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />
<cfset tries = 0 />
<cfset combos = 0 />
<cfoutput>
<cfloop from="1" to="6" index="b">
#testCombo(apps[b].name, apps[b].cost, apps)#
</cfloop>
<br />
tries: #tries#<br />
combos: #combos#
</cfoutput>
sortie:
Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit,Mixed Fruit = 15.05
Mixed Fruit,hot wings,hot wings,sampler plate = 15.05
Mixed Fruit,hot wings,sampler plate,hot wings = 15.05
Mixed Fruit,sampler plate,hot wings,hot wings = 15.05
false false false hot wings,Mixed Fruit,hot wings,sampler plate = 15.05
hot wings,Mixed Fruit,sampler plate,hot wings = 15.05
hot wings,hot wings,Mixed Fruit,sampler plate = 15.05
hot wings,sampler plate,Mixed Fruit,hot wings = 15.05
false false sampler plate,Mixed Fruit,hot wings,hot wings = 15.05
sampler plate,hot wings,Mixed Fruit,hot wings = 15.05
false
tries: 2014
combos: 12067
je pense que cela peut avoir toutes les combinaisons correctes, mais ma question tient toujours: y a-t-il une meilleure algorithme?
apprendre de réponse de @rcar , et un autre remaniement plus tard, j'ai le suivant.
comme avec tant de choses que je code, je me suis refactorisé de CFML à CFScript, mais le code est essentiellement le même.
j'ai ajouté dans sa suggestion d'un point de départ dynamique dans le tableau (au lieu de passer le tableau par valeur et de changer sa valeur pour les récursions futures), ce qui m'a amené aux mêmes statistiques qu'il obtient (209 récursions, 571 les vérifications de prix de combinaison (itérations de boucle), et puis amélioré sur cela en supposant que le tableau sera trié par coût -- parce qu'il est -- et de rompre dès que nous allons au-dessus du prix cible. Avec la rupture, il nous en reste 209 récursions et 376 itérations en boucle.
quelles autres améliorations pourrait-on apporter à l'algorithme?
function testCombo(minIndex, currentCombo, currentTotal){
var a = 0;
var CC = "";
var CT = 0;
var found = false;
tries += 1;
for (a=arguments.minIndex; a <= arrayLen(apps); a++){
combos += 1;
CC = listAppend(arguments.currentCombo, apps[a].name);
CT = arguments.currentTotal + apps[a].cost;
if (CT eq 15.05){
//print current combo
WriteOutput("<strong>#CC# = 15.05</strong><br />");
return(true);
}else if (CT gt 15.05){
//since we know the array is sorted by cost (asc),
//and we've already gone over the price limit,
//we can ignore anything else in the array
break;
}else{
//less than 15.50, try adding something else
found = testCombo(a, CC, CT);
}
}
return(found);
}
mf = {name="mixed fruit", cost=2.15};
ff = {name="french fries", cost=2.75};
ss = {name="side salad", cost=3.35};
hw = {name="hot wings", cost=3.55};
ms = {name="mozarella sticks", cost=4.20};
sp = {name="sampler plate", cost=5.80};
apps = [ mf, ff, ss, hw, ms, sp ];
tries = 0;
combos = 0;
testCombo(1, "", 0);
WriteOutput("<br />tries: #tries#<br />combos: #combos#");
voici l'implémentation simultanée dans Clojure. Pour calculer (items-with-price 15.05) prend environ 14 récursions de génération de combinaison, et environ 10 contrôles de possibilité. Il m'a fallu environ 6 minutes pour calculer (items-with-price 100) sur mon Intel Q9300.
cela donne seulement la première réponse trouvée, ou nil s'il n'y en a pas, comme c'est tout le problème appelle. Pourquoi faire plus de travail qu'on vous a demandé de faire ;) ?
;; np-complete.clj
;; A Clojure solution to XKCD #287 "NP-Complete"
;; By Sam Fredrickson
;;
;; The function "items-with-price" returns a sequence of items whose sum price
;; is equal to the given price, or nil.
(defstruct item :name :price)
(def *items* #{(struct item "Mixed Fruit" 2.15)
(struct item "French Fries" 2.75)
(struct item "Side Salad" 3.35)
(struct item "Hot Wings" 3.55)
(struct item "Mozzarella Sticks" 4.20)
(struct item "Sampler Plate" 5.80)})
(defn items-with-price [price]
(let [check-count (atom 0)
recur-count (atom 0)
result (atom nil)
checker (agent nil)
; gets the total price of a seq of items.
items-price (fn [items] (apply + (map #(:price %) items)))
; checks if the price of the seq of items matches the sought price.
; if so, it changes the result atom. if the result atom is already
; non-nil, nothing is done.
check-items (fn [unused items]
(swap! check-count inc)
(if (and (nil? @result)
(= (items-price items) price))
(reset! result items)))
; lazily generates a list of combinations of the given seq s.
; haven't tested well...
combinations (fn combinations [cur s]
(swap! recur-count inc)
(if (or (empty? s)
(> (items-price cur) price))
'()
(cons cur
(lazy-cat (combinations (cons (first s) cur) s)
(combinations (cons (first s) cur) (rest s))
(combinations cur (rest s))))))]
; loops through the combinations of items, checking each one in a thread
; pool until there are no more combinations or the result atom is non-nil.
(loop [items-comb (combinations '() (seq *items*))]
(if (and (nil? @result)
(not-empty items-comb))
(do (send checker check-items (first items-comb))
(recur (rest items-comb)))))
(await checker)
(println "No. of recursions:" @recur-count)
(println "No. of checks:" @check-count)
@result))
Si vous voulez un algorithme optimisé, il est préférable d'essayer les prix dans l'ordre décroissant. Qui vous permet d'utiliser autant de la quantité restante d'abord et ensuite voir comment le reste peut être rempli.
aussi, vous pouvez utiliser les mathématiques pour comprendre la quantité maximale de chaque aliment pour commencer chaque fois afin que vous n'essayez pas des combinaisons qui dépasseraient le but de 15,05$.
cet algorithme a seulement besoin d'essayer 88 combinaisons pour obtenir une réponse complète et cela ressemble au plus bas qui a été affiché jusqu'à présent:
public class NPComplete {
private static final int[] FOOD = { 580, 420, 355, 335, 275, 215 };
private static int tries;
public static void main(String[] ignore) {
tries = 0;
addFood(1505, "", 0);
System.out.println("Combinations tried: " + tries);
}
private static void addFood(int goal, String result, int index) {
// If no more food to add, see if this is a solution
if (index >= FOOD.length) {
tries++;
if (goal == 0)
System.out.println(tries + " tries: " + result.substring(3));
return;
}
// Try all possible quantities of this food
// If this is the last food item, only try the max quantity
int qty = goal / FOOD[index];
do {
addFood(goal - qty * FOOD[index],
result + " + " + qty + " * " + FOOD[index], index + 1);
} while (index < FOOD.length - 1 && --qty >= 0);
}
}
Voici la sortie montrant les deux solutions:
9 tries: 1 * 580 + 0 * 420 + 2 * 355 + 0 * 335 + 0 * 275 + 1 * 215 88 tries: 0 * 580 + 0 * 420 + 0 * 355 + 0 * 335 + 0 * 275 + 7 * 215 Combinations tried: 88