Lissage des valeurs au fil du temps: moyenne mobile ou quelque chose de mieux?
Je Code quelque chose au moment où je prends un tas de valeurs au fil du temps à partir d'une boussole matérielle. Cette boussole est très précise et se met à jour très souvent, avec le résultat que si elle bouge légèrement, je me retrouve avec la valeur étrange qui est sauvagement incompatible avec ses voisins. Je veux adoucir ces valeurs.
après avoir fait quelques lectures, il semblerait que ce que je veux, c'est un filtre passe-haut, un filtre passe-bas ou une moyenne mobile. Déménagement moyenne je peux descendre avec, juste garder un historique des 5 dernières valeurs ou peu importe, et utiliser la moyenne de ces valeurs en aval dans mon code où j'ai été une fois juste en utilisant la valeur la plus récente.
qui devrait, je pense, lisser ces jiggles bien, mais il me frappe que c'est probablement tout à fait inefficace, et c'est probablement l'un de ces problèmes connus pour les programmeurs appropriés à laquelle il ya une solution mathématique intelligente vraiment soignée.
je suis, cependant, l'un de ces affreux programmeurs autodidactes sans éducation formelle dans quoi que ce soit, même vaguement lié à CompSci ou les mathématiques. Un peu de lecture suggère que cela peut être un filtre passe haut ou bas, mais je ne trouve rien qui explique en termes compréhensibles pour un hack comme moi ce que l'effet de ces algorithmes serait sur un tableau de valeurs, et encore moins comment les mathématiques fonctionne. La réponse donnée ici , par exemple, techniquement répond à ma question, mais seulement en termes compréhensibles pour ceux qui savez probablement déjà comment résoudre le problème.
ce serait une personne très charmante et intelligente qui pourrait expliquer le genre de problème que c'est, et comment les solutions fonctionnent, en termes compréhensibles pour un diplômé en Arts.
5 réponses
si votre moyenne mobile doit être longue pour obtenir le lissage requis, et que vous n'avez pas vraiment besoin d'une forme particulière du noyau, alors vous êtes mieux si vous utilisez une moyenne mobile qui se décompose exponentiellement:
a(i+1) = tiny*data(i+1) + (1.0-tiny)*a(i)
où vous choisissez tiny pour être une constante appropriée (par exemple si vous choisissez tiny = 1 - 1/N, il aura la même quantité de moyenne comme une fenêtre de taille N, mais distribué différemment sur les points plus anciens).
de toute façon, puisque la valeur suivante de la moyenne mobile dépend seulement de la précédente et de vos données, vous n'avez pas à garder une queue ou quoi que ce soit. Et vous pouvez penser à quelque chose comme, "Eh bien, j'ai un nouveau point, mais je n'y crois pas vraiment, donc je vais garder 80% de mon ancienne estimation de la mesure, et ne faire confiance à ce nouveau point de données que 20%". C'est à peu près la même chose que de dire, "Eh bien, je ne fais confiance à ce nouveau point 20%, et je vais utiliser 4 autres points que je fais confiance à la même montant", sauf qu'au lieu de prendre explicitement les 4 autres points, vous supposez que la moyenne que vous avez fait la dernière fois était raisonnable de sorte que vous pouvez utiliser votre travail précédent.
si vous essayez de supprimer la valeur impaire occasionnelle, un filtre passe-bas est la meilleure des trois options que vous avez identifiées. Les filtres passe-bas permettent des changements de vitesse tels que ceux causés par la rotation manuelle d'une boussole, tout en rejetant les changements de vitesse tels que ceux causés par des bosses sur la route, par exemple.
une moyenne mobile ne sera probablement pas suffisante, car les effets d'un seul "blip" dans vos données affecteront plusieurs valeurs, en fonction de la taille de votre fenêtre moyenne mobile.
si les valeurs impaires sont facilement détectables, vous pouvez même être mieux avec un algorithme de suppression des défauts qui les ignore complètement:
if (abs(thisValue - averageOfLast10Values) > someThreshold)
{
thisValue = averageOfLast10Values;
}
voici un graphique de guick pour illustrer:
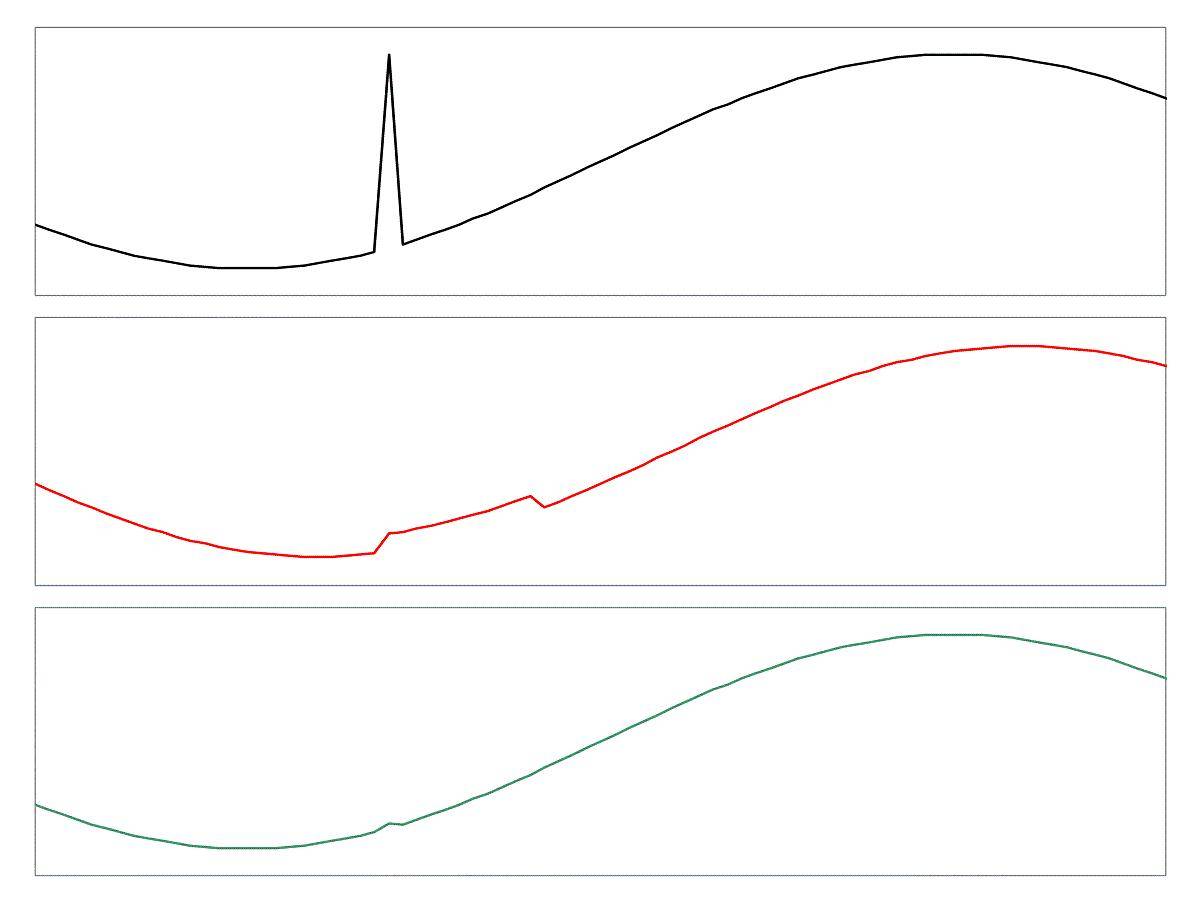
le premier graphique est le signal d'entrée, avec un bug désagréable. Le deuxième graphique montre l'effet d'un déplacement de 10 échantillons moyen. Le graphique final est une combinaison de la moyenne de 10 échantillons et de l'algorithme simple de détection de bug illustré ci-dessus. Lorsque le problème est détecté, la moyenne de 10 échantillons est utilisée à la place de la valeur réelle.
moyenne mobile je peux descendre avec ... mais il me semble que c'est probablement tout à fait inefficace.
il n'y a vraiment aucune raison qu'une moyenne mobile soit inefficace. Vous gardez le nombre de points de données que vous voulez dans un tampon (comme une file circulaire). Sur chaque nouveau point de données, vous insérez la valeur la plus ancienne et la soustrayez d'une somme, et poussez la plus récente et ajoutez-la à la somme. Donc chaque nouveau point de données ne nécessite vraiment qu'un pop / push, un addition et une soustraction. Votre moyenne mobile est toujours ce décalage somme divisée par le nombre de valeurs dans votre tampon.
il obtient un petit plus difficile si vous recevez des données en même temps de multiples threads, mais puisque vos données proviennent d'un dispositif matériel qui semble très douteux pour moi.
OH et aussi: d'horribles programmeurs autodidactes s'unissent! ;)
une moyenne mobile décroissant exponentiellement peut être calculée "à la main" avec seulement la tendance si vous utilisez les valeurs appropriées. Voir http://www.fourmilab.ch/hackdiet/e4/ pour avoir une idée sur la manière de le faire rapidement avec un stylo et du papier si vous êtes à la recherche pour "de façon exponentielle lissés en moyenne mobile à 10% de lissage". Mais puisque vous avez un ordinateur, vous voulez probablement faire le déplacement binaire par opposition au déplacement décimal ;)
par ici, vous tous besoin d'une variable pour votre valeur actuelle et l'autre pour la moyenne. La moyenne suivante peut alors être calculée à partir de cela.
il y a une technique appelée Porte de gamme qui fonctionne bien avec les échantillons non essentiels de faible fréquence. en supposant l'utilisation de l'une des techniques de filtre mentionnées ci-dessus (moyenne mobile, exponentielle), une fois que vous avez "suffisant" l'histoire (une constante de temps) vous pouvez tester le nouvel échantillon de données entrantes pour la vraisemblance, avant il est ajouté au calcul.
il faut avoir une certaine connaissance de la vitesse de changement maximale raisonnable du signal. l'échantillon brut est comparé à la valeur lissée la plus récente, et si la valeur absolue de cette différence est supérieure à la fourchette permise, l'échantillon est jeté (ou remplacé par une valeur heuristique, par exemple). une prédiction basée sur la pente; différentielle ou la "tendance" de prédiction de la valeur de la double lissage exponentiel)