Données de lissage dans la courbe de Contour avec Matplotlib
je travaille sur la création d'un tracé de contour en utilisant Matplotlib. J'ai toutes les données dans un tableau multidimensionnel. Il est 12 long environ 2000 large. Donc, il est en fait une liste de 12 listes de 2000 dans la longueur. J'ai le contour de la parcelle ça marche, mais je dois lisser les données. J'ai lu beaucoup de exemple. Malheureusement, je n'ai pas le bagage mathématique pour comprendre ce qui est passe avec eux.
alors, comment puis-je lisser ces données? J'ai un exemple de à quoi ressemble mon graphique et ce que je veux que ça ressemble plus à ça.
C'est mon graphe:
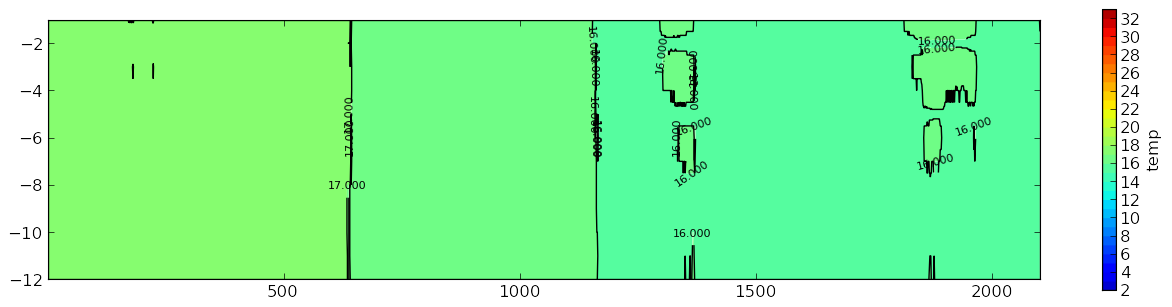
Ce que je veux qu'il ressemble plus trop similaire:
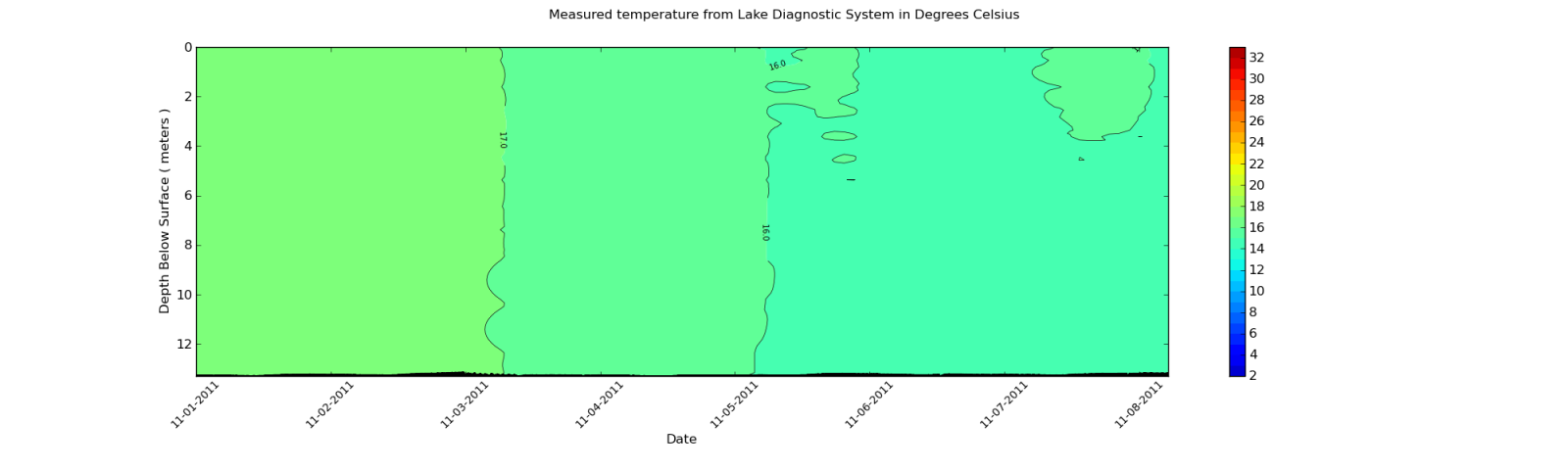
Qu'est-ce que cela signifie que je dois lisser le tracé du contour comme dans la deuxième parcelle?
les données que j'utilise sont extraites d'un fichier XML. Mais, je vais montrer la sortie de une partie de la matrice. Comme chaque élément du tableau est d'environ 2000 articles de long, I affiche seulement un extrait.
voici un échantillon:
[27.899999999999999, 27.899999999999999, 27.899999999999999, 27.899999999999999,
28.0, 27.899999999999999, 27.899999999999999, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.0, 28.100000000000001, 28.100000000000001,
28.0, 28.100000000000001, 28.100000000000001, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.100000000000001, 28.100000000000001,
28.100000000000001, 28.100000000000001, 28.0, 27.899999999999999, 28.0,
27.899999999999999, 27.800000000000001, 27.899999999999999, 27.800000000000001,
27.800000000000001, 27.800000000000001, 27.899999999999999, 27.899999999999999, 28.0,
27.800000000000001, 27.800000000000001, 27.800000000000001, 27.899999999999999,
27.899999999999999, 27.899999999999999, 27.899999999999999, 28.0, 28.0, 28.0, 28.0,
28.0, 28.0, 28.0, 28.0, 27.899999999999999, 28.0, 28.0, 28.0, 28.0, 28.0,
28.100000000000001, 28.0, 28.0, 28.100000000000001, 28.199999999999999,
28.300000000000001, 28.300000000000001, 28.300000000000001, 28.300000000000001,
28.300000000000001, 28.399999999999999, 28.300000000000001, 28.300000000000001,
28.300000000000001, 28.300000000000001, 28.300000000000001, 28.300000000000001,
28.399999999999999, 28.399999999999999, 28.399999999999999, 28.399999999999999,
28.399999999999999, 28.300000000000001, 28.399999999999999, 28.5, 28.399999999999999,
28.399999999999999, 28.399999999999999, 28.399999999999999]
gardez à l'esprit que ceci n'est qu'un extrait. La dimension des données est de 12 lignes par 1959 colonnes. Les colonnes changent selon les données importées du XML fichier. Je peux regarder les valeurs après que j'ai utilisé le Gaussian_filter et ils font changement. Mais, les changements ne sont pas assez grandes pour affecter le contour de la parcelle.
2 réponses
vous pourriez lisser vos données avec un gaussian_filter :
import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage as ndimage
X, Y = np.mgrid[-70:70, -70:70]
Z = np.cos((X**2+Y**2)/200.)+ np.random.normal(size=X.shape)
# Increase the value of sigma to increase the amount of blurring.
# order=0 means gaussian kernel
Z2 = ndimage.gaussian_filter(Z, sigma=1.0, order=0)
fig=plt.figure()
ax=fig.add_subplot(1,2,1)
ax.imshow(Z)
ax=fig.add_subplot(1,2,2)
ax.imshow(Z2)
plt.show()
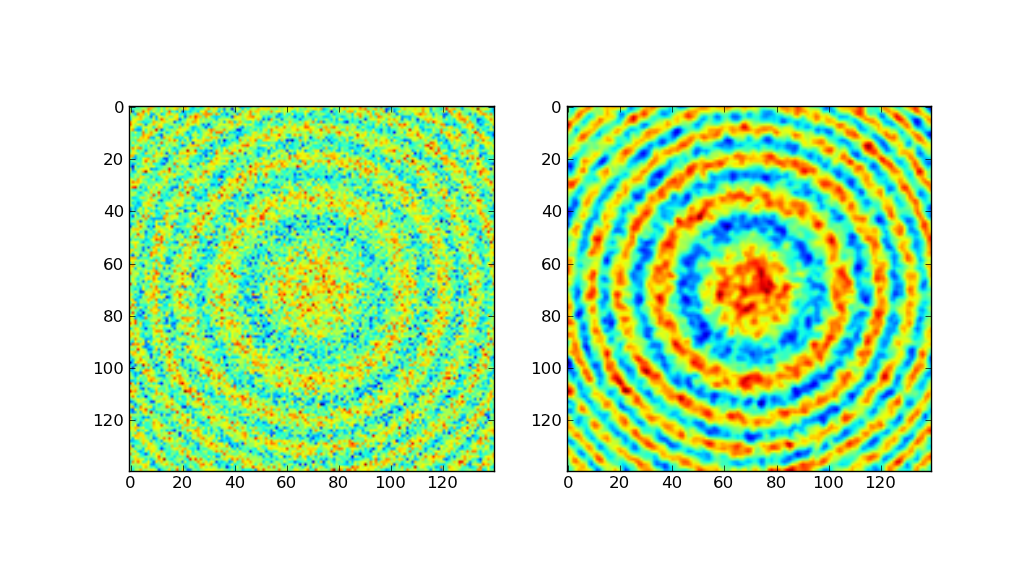
le côté gauche montre les données originales, le côté droit après le filtrage gaussien.
une grande partie du code ci-dessus est tirée du Scipy Cookbook , qui montre un lissage gaussien à l'aide d'un grain gaussien fabriqué à la main. Puisque scipy est livré avec le même intégré, j'ai choisi pour utiliser gaussian_filter .
une façon facile de lisser les données est d'utiliser un moyenne mobile algorithme. Une simple forme de moyenne mobile est de calculer la moyenne des mesures adjacentes à une certaine position. Dans une dimension d'une série de mesures a[1:N], par exemple, la moyenne mobile à un[n] peut être calculé comme[n] = (a[n-1] + a[n] + a[n+1]) / 3, par exemple. Si vous prenez toutes vos mesures, c'est fini. Dans cet exemple simple, notre fenêtre de moyenne a la taille 3. Vous peut également utiliser des fenêtres de différentes tailles, en fonction de la quantité de lissage que vous voulez.
pour faciliter et accélérer les calculs pour un plus large éventail d'applications, vous pouvez également utiliser un algorithme basé sur convolution . L'avantage de l'utilisation de convolution est que vous pouvez choisir différents types de moyennes, comme des moyennes pondérées, en changeant simplement la fenêtre.
donnons quelques codes pour illustrer. L'extrait suivant besoins Numpy, Matplotlib et Scipy installés. Cliquez ici pour le code d'échantillon complet
from __future__ import division
import numpy
import pylab
from scipy.signal import convolve2d
def moving_average_2d(data, window):
"""Moving average on two-dimensional data.
"""
# Makes sure that the window function is normalized.
window /= window.sum()
# Makes sure data array is a numpy array or masked array.
if type(data).__name__ not in ['ndarray', 'MaskedArray']:
data = numpy.asarray(data)
# The output array has the same dimensions as the input data
# (mode='same') and symmetrical boundary conditions are assumed
# (boundary='symm').
return convolve2d(data, window, mode='same', boundary='symm')
le code suivant génère des données arbitraires et bruyantes, puis calcule la moyenne mobile à l'aide de quatre fenêtres de taille différente.
M, N = 20, 2000 # The shape of the data array
m, n = 3, 10 # The shape of the window array
y, x = numpy.mgrid[1:M+1, 0:N]
# The signal and lots of noise
signal = -10 * numpy.cos(x / 500 + y / 10) / y
noise = numpy.random.normal(size=(M, N))
z = signal + noise
# Calculating a couple of smoothed data.
win = numpy.ones((m, n))
z1 = moving_average_2d(z, win)
win = numpy.ones((2*m, 2*n))
z2 = moving_average_2d(z, win)
win = numpy.ones((2*m, 4*n))
z3 = moving_average_2d(z, win)
win = numpy.ones((2*m, 10*n))
z4 = moving_average_2d(z, win)
Et puis, pour voir les différents résultats, voici le code pour certains de traçage.
# Initializing the plot
pylab.close('all')
pylab.ion()
fig = pylab.figure()
bbox = dict(edgecolor='w', facecolor='w', alpha=0.9)
crange = numpy.arange(-15, 16, 1.) # color scale data range
# The plots
ax = pylab.subplot(2, 2, 1)
pylab.contourf(x, y, z, crange)
pylab.contour(x, y, z1, crange, colors='k')
ax.text(0.05, 0.95, 'n=10, m=3', ha='left', va='top', transform=ax.transAxes,
bbox=bbox)
bx = pylab.subplot(2, 2, 2, sharex=ax, sharey=ax)
pylab.contourf(x, y, z, crange)
pylab.contour(x, y, z2, crange, colors='k')
bx.text(0.05, 0.95, 'n=20, m=6', ha='left', va='top', transform=bx.transAxes,
bbox=bbox)
bx = pylab.subplot(2, 2, 3, sharex=ax, sharey=ax)
pylab.contourf(x, y, z, crange)
pylab.contour(x, y, z3, crange, colors='k')
bx.text(0.05, 0.95, 'n=40, m=6', ha='left', va='top', transform=bx.transAxes,
bbox=bbox)
bx = pylab.subplot(2, 2, 4, sharex=ax, sharey=ax)
pylab.contourf(x, y, z, crange)
pylab.contour(x, y, z4, crange, colors='k')
bx.text(0.05, 0.95, 'n=100, m=6', ha='left', va='top', transform=bx.transAxes,
bbox=bbox)
ax.set_xlim([x.min(), x.max()])
ax.set_ylim([y.min(), y.max()])
fig.savefig('movingavg_sample.png')
# That's all folks!
et voici les résultats tracés pour différents taille des fenêtres: 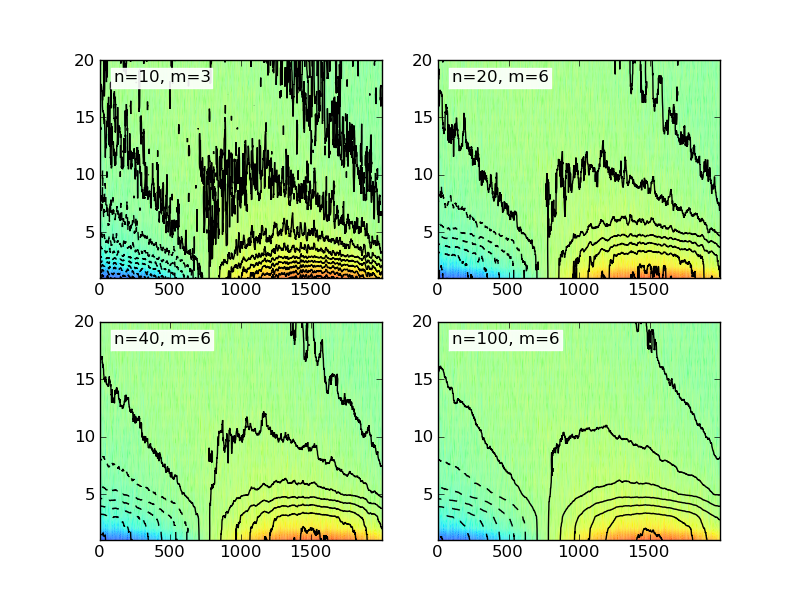
l'exemple de code donné ici utilise une fenêtre simple (ou rectangulaire) en deux dimensions. Il existe plusieurs types de fenêtres disponibles et vous pourriez vouloir vérifier Wikipedia pour plus d'exemples.