Lissage d'une courbe dessinée à la main

La réponse de Kris est un très bon port de L'original en C#, mais la performance n'est pas idéale et il y a des endroits où l'instabilité en virgule flottante peut causer des problèmes et renvoyer des valeurs NaN (cela est également vrai dans le code original). J'ai créé une bibliothèque qui contient mon propre port de celui-ci ainsi que Ramer-Douglas-Peuker, et devrait fonctionner non seulement avec les points WPF, mais les nouveaux types de vecteurs SIMD et Unity 3D aussi:

Https://github.com/burningmime/curves

Peut-être que cet article basé sur WPF + Bezier est un bon début: Dessinez une courbe lisse à travers un ensemble de Points 2D avec des Primitives Bezier

Eh bien, le travail de Kris était très utile.

J'ai réalisé que le problème qu'il a signalé à propos de l'algorithme se terminant plus tôt en raison d'une erreur mal calculée se terminant sur 0, est dû au fait qu'un point est répété et la tangente calculée est infinie.

J'ai fait une traduction en Java, basée sur le code de Kris, ça marche bien je crois:

Modifier:

Je travaille toujours et j'essaie d'obtenir un meilleur comportement sur l'algorithme. J'ai réalisé que sur très spiky angles, Les courbes de Bézier ne se comportent tout simplement pas bien. J'ai donc essayé de combiner des courbes de Bézier avec des lignes et c'est le résultat:

import java.awt.Point;
import java.awt.Shape;
import java.awt.geom.CubicCurve2D;
import java.awt.geom.Line2D;
import java.awt.geom.Point2D;
import java.util.LinkedList;
import java.util.List;
import java.util.concurrent.atomic.AtomicInteger;

import javax.vecmath.Point2d;
import javax.vecmath.Tuple2d;
import javax.vecmath.Vector2d;



/*
An Algorithm for Automatically Fitting Digitized Curves
by Philip J. Schneider
from "Graphics Gems", Academic Press, 1990
*/
public class FitCurves
{
/*  Fit the Bezier curves */

private final static int MAXPOINTS = 10000;
private final static double epsilon = 1.0e-6;

/**
 * Rubén:
 * This is the sensitivity. When it is 1, it will create a line if it is at least as long as the
 * distance from the previous control point.
 * When it is greater, it will create less lines, and when it is lower, more lines.
 * This is based on the previous control point since I believe it is a good indicator of the curvature
 * where it is coming from, and we don't want long and second derived constant curves to be modeled with
 * many lines.
 */
private static final double lineSensitivity=0.75;




public interface ResultCurve {
    public Point2D getStart();
    public Point2D getEnd();
    public Shape getShape();
}

public static class BezierCurve implements ResultCurve {
    public Point start;
    public Point end;
    public Point ctrl1;
    public Point ctrl2;
    public BezierCurve(Point2D start, Point2D ctrl1, Point2D ctrl2, Point2D end) {
        this.start=new Point((int)Math.round(start.getX()), (int)Math.round(start.getY()));
        this.end=new Point((int)Math.round(end.getX()), (int)Math.round(end.getY()));
        this.ctrl1=new Point((int)Math.round(ctrl1.getX()), (int)Math.round(ctrl1.getY()));
        this.ctrl2=new Point((int)Math.round(ctrl2.getX()), (int)Math.round(ctrl2.getY()));
        if(this.ctrl1.x<=1 || this.ctrl1.y<=1) {
            throw new IllegalStateException("ctrl1 invalid");
        }
        if(this.ctrl2.x<=1 || this.ctrl2.y<=1) {
            throw new IllegalStateException("ctrl2 invalid");
        }
    }
    public Shape getShape() {
        return new CubicCurve2D.Float(start.x, start.y, ctrl1.x, ctrl1.y, ctrl2.x, ctrl2.y, end.x, end.y);
    }
    public Point getStart() {
        return start;
    }
    public Point getEnd() {
        return end;
    }
}

public static class CurveSegment implements ResultCurve {
    Point2D start;
    Point2D end;
    public CurveSegment(Point2D startP, Point2D endP) {
        this.start=startP;
        this.end=endP;
    }
    public Shape getShape() {
        return new Line2D.Float(start, end);
    }
    public Point2D getStart() {
        return start;
    }
    public Point2D getEnd() {
        return end;
    }
}


public static List<ResultCurve> FitCurve(double[][] points, double error) {
    Point[] allPoints=new Point[points.length]; 
    for(int i=0; i < points.length; i++) {
        allPoints[i]=new Point((int) Math.round(points[i][0]), (int) Math.round(points[i][1]));
    }
    return FitCurve(allPoints, error);
}

public static List<ResultCurve> FitCurve(Point[] d, double error)
{
    Vector2d tHat1, tHat2;    /*  Unit tangent vectors at endpoints */

    int first=0;
    int last=d.length-1;
    tHat1 = ComputeLeftTangent(d, first);
    tHat2 = ComputeRightTangent(d, last);
    List<ResultCurve> result = new LinkedList<ResultCurve>();
    FitCubic(d, first, last, tHat1, tHat2, error, result);

    return result;
}


private static void FitCubic(Point[] d, int first, int last, Vector2d tHat1, Vector2d tHat2, double error, List<ResultCurve> result)
{
    PointE[] bezCurve; /*Control points of fitted Bezier curve*/
    double[] u;     /*  Parameter values for point  */
    double[] uPrime;    /*  Improved parameter values */
    double maxError;    /*  Maximum fitting error    */
    int nPts;       /*  Number of points in subset  */
    double iterationError; /*Error below which you try iterating  */
    int maxIterations = 4; /*  Max times to try iterating  */
    Vector2d tHatCenter;      /* Unit tangent vector at splitPoint */
    int i;
    double errorOnLine=error;

    iterationError = error * error;
    nPts = last - first + 1;

    AtomicInteger outputSplitPoint=new AtomicInteger();

    /**
     * Rubén: Here we try to fit the form with a line, and we mark the split point if we find any line with a minimum length
     */
    /*
     * the minimum distance for a length (so we don't create a very small line, when it could be slightly modeled with the previous Bezier,
     * will be proportional to the distance of the previous control point of the last Bezier.
     */
    BezierCurve res=null;
    for(i=result.size()-1; i >0; i--) {
        ResultCurve thisCurve=result.get(i);
        if(thisCurve instanceof BezierCurve) {
            res=(BezierCurve)thisCurve;
            break;
        }
    }


    Line seg=new Line(d[first], d[last]);
    int nAcceptableTogether=0;
    int startPoint=-1;
    int splitPointTmp=-1;

    if(Double.isInfinite(seg.getGradient())) {
        for (i = first; i <= last; i++) {
            double dist=Math.abs(d[i].x-d[first].x);
            if(dist<errorOnLine) {
                nAcceptableTogether++;
                if(startPoint==-1) startPoint=i;
            } else {
                if(startPoint!=-1) {
                    double minLineLength=Double.POSITIVE_INFINITY;
                    if(res!=null) {
                        minLineLength=lineSensitivity * res.ctrl2.distance(d[startPoint]);
                    }
                    double thisFromStart=d[startPoint].distance(d[i]);
                    if(thisFromStart >= minLineLength) {
                        splitPointTmp=i;
                        startPoint=-1;
                        break;
                    }
                }
                nAcceptableTogether=0;
                startPoint=-1;
            }
        }
    } else {
        //looking for the max squared error
        for (i = first; i <= last; i++) {
            Point thisPoint=d[i];
            Point2D calculatedP=seg.getByX(thisPoint.getX());
            double dist=thisPoint.distance(calculatedP);
            if(dist<errorOnLine) {
                nAcceptableTogether++;
                if(startPoint==-1) startPoint=i;
            } else {
                if(startPoint!=-1) {
                    double thisFromStart=d[startPoint].distance(thisPoint);
                    double minLineLength=Double.POSITIVE_INFINITY;
                    if(res!=null) {
                        minLineLength=lineSensitivity * res.ctrl2.distance(d[startPoint]);
                    }
                    if(thisFromStart >= minLineLength) {
                        splitPointTmp=i;
                        startPoint=-1;
                        break;
                    }
                }
                nAcceptableTogether=0;
                startPoint=-1;
            }
        }
    }

    if(startPoint!=-1) {
        double minLineLength=Double.POSITIVE_INFINITY;
        if(res!=null) {
            minLineLength=lineSensitivity * res.ctrl2.distance(d[startPoint]);
        }
        if(d[startPoint].distance(d[last]) >= minLineLength) {
            splitPointTmp=startPoint;
            startPoint=-1;
        } else {
            nAcceptableTogether=0;
        }
    }
    outputSplitPoint.set(splitPointTmp);

    if(nAcceptableTogether==(last-first+1)) {
        //This is a line!
        System.out.println("line, length: " + d[first].distance(d[last]));
        result.add(new CurveSegment(d[first], d[last]));
        return;
    }

    /*********************** END of the Line approach, lets try the normal algorithm *******************************************/


    if(splitPointTmp < 0) {
        if(nPts == 2) {
            double dist = d[first].distance(d[last]) / 3.0;  //sqrt((last.x-first.x)^2 + (last.y-first.y)^2) / 3.0   
            bezCurve = new PointE[4];
            bezCurve[0] = new PointE(d[first]);
            bezCurve[3] = new PointE(d[last]);
            bezCurve[1]=new PointE(tHat1).scaleAdd(dist, bezCurve[0]); //V2Add(&bezCurve[0], V2Scale(&tHat1, dist), &bezCurve[1]);
            bezCurve[2]=new PointE(tHat2).scaleAdd(dist, bezCurve[3]); //V2Add(&bezCurve[3], V2Scale(&tHat2, dist), &bezCurve[2]);

            result.add(new BezierCurve(bezCurve[0],bezCurve[1],bezCurve[2],bezCurve[3]));
            return;
        }


        /*  Parameterize points, and attempt to fit curve */
        u = ChordLengthParameterize(d, first, last);
        bezCurve = GenerateBezier(d, first, last, u, tHat1, tHat2);

        /*  Find max deviation of points to fitted curve */
        maxError = ComputeMaxError(d, first, last, bezCurve, u, outputSplitPoint);
        if(maxError < error) {
            result.add(new BezierCurve(bezCurve[0],bezCurve[1],bezCurve[2],bezCurve[3]));
            return;
        }


        /*  If error not too large, try some reparameterization  */
        /*  and iteration */
        if(maxError < iterationError)
        {
            for(i = 0; i < maxIterations; i++) {
                uPrime = Reparameterize(d, first, last, u, bezCurve);
                bezCurve = GenerateBezier(d, first, last, uPrime, tHat1, tHat2);
                maxError = ComputeMaxError(d, first, last, bezCurve, uPrime, outputSplitPoint);
                if(maxError < error) {
                    result.add(new BezierCurve(bezCurve[0],bezCurve[1],bezCurve[2],bezCurve[3]));
                    return;
                }
                u = uPrime;
            }
        }
    }

    /* Fitting failed -- split at max error point and fit recursively */
    tHatCenter = ComputeCenterTangent(d, outputSplitPoint.get());
    FitCubic(d, first, outputSplitPoint.get(), tHat1, tHatCenter, error,result);
    tHatCenter.negate();
    FitCubic(d, outputSplitPoint.get(), last, tHatCenter, tHat2, error,result);
}

//Checked!!
static PointE[] GenerateBezier(Point2D[] d, int first, int last, double[] uPrime, Vector2d tHat1, Vector2d tHat2)
{
    int     i;
    Vector2d[][] A = new Vector2d[MAXPOINTS][2];    /* Precomputed rhs for eqn    */

    int     nPts;           /* Number of pts in sub-curve */
    double[][]  C = new double[2][2];            /* Matrix C     */
    double[]    X = new double[2];          /* Matrix X         */
    double  det_C0_C1,      /* Determinants of matrices */
            det_C0_X,
            det_X_C1;
    double  alpha_l,        /* Alpha values, left and right */
            alpha_r;          
    PointE[] bezCurve = new PointE[4];    /* RETURN bezier curve ctl pts  */
    nPts = last - first + 1;

    /* Compute the A's  */
        for (i = 0; i < nPts; i++) {
            Vector2d v1=new Vector2d(tHat1);
            Vector2d v2=new Vector2d(tHat2);
            v1.scale(B1(uPrime[i]));
            v2.scale(B2(uPrime[i]));
            A[i][0] = v1;
            A[i][1] = v2;
        }

        /* Create the C and X matrices  */
        C[0][0] = 0.0;
        C[0][1] = 0.0;
        C[1][0] = 0.0;
        C[1][1] = 0.0;
        X[0]    = 0.0;
        X[1]    = 0.0;

        for (i = 0; i < nPts; i++) {
            C[0][0] += A[i][0].dot(A[i][0]);    //C[0][0] += V2Dot(&A[i][0], &A[i][0]);
            C[0][1] += A[i][0].dot(A[i][1]);    //C[0][1] += V2Dot(&A[i][0], &A[i][1]);
    /*                  C[1][0] += V2Dot(&A[i][0], &A[i][9]);*/ 
            C[1][0] = C[0][1];  //C[1][0] = C[0][1]
            C[1][1] += A[i][1].dot(A[i][1]);    //C[1][1] += V2Dot(&A[i][1], &A[i][1]);

            Tuple2d scaleLastB2=new Vector2d(PointE.getPoint2d(d[last])); scaleLastB2.scale(B2(uPrime[i])); // V2ScaleIII(d[last], B2(uPrime[i]))
            Tuple2d scaleLastB3=new Vector2d(PointE.getPoint2d(d[last])); scaleLastB3.scale(B3(uPrime[i])); // V2ScaleIII(d[last], B3(uPrime[i]))
            Tuple2d dLastB2B3Sum=new Vector2d(scaleLastB2); dLastB2B3Sum.add(scaleLastB3);  //V2AddII(V2ScaleIII(d[last], B2(uPrime[i])), V2ScaleIII(d[last], B3(uPrime[i]))

            Tuple2d scaleFirstB1=new Vector2d(PointE.getPoint2d(d[first])); scaleFirstB1.scale(B1(uPrime[i]));  //V2ScaleIII(d[first], B1(uPrime[i]))

            Tuple2d sumScaledFirstB1andB2B3=new Vector2d(scaleFirstB1); sumScaledFirstB1andB2B3.add(dLastB2B3Sum);  //V2AddII(V2ScaleIII(d[first], B1(uPrime[i])), V2AddII(V2ScaleIII(d[last], B2(uPrime[i])), V2ScaleIII(d[last], B3(uPrime[i])))

            Tuple2d scaleFirstB0=new Vector2d(PointE.getPoint2d(d[first])); scaleFirstB0.scale(B0(uPrime[i]));      //V2ScaleIII(d[first], B0(uPrime[i])
            Tuple2d sumB0Rest=new Vector2d(scaleFirstB0); sumB0Rest.add(sumScaledFirstB1andB2B3);       //V2AddII(V2ScaleIII(d[first], B0(uPrime[i])), V2AddII( V2ScaleIII(d[first], B1(uPrime[i])), V2AddII(V2ScaleIII(d[last], B2(uPrime[i])), V2ScaleIII(d[last], B3(uPrime[i]))))));

            Vector2d tmp=new Vector2d(PointE.getPoint2d(d[first + i]));
            tmp.sub(sumB0Rest);

            X[0] += A[i][0].dot(tmp);
            X[1] += A[i][1].dot(tmp);
        }

        /* Compute the determinants of C and X  */
        det_C0_C1 = C[0][0] * C[1][1] - C[1][0] * C[0][1];
        det_C0_X  = C[0][0] * X[1]    - C[1][0] * X[0];
        det_X_C1  = X[0]    * C[1][1] - X[1]    * C[0][1];

        /* Finally, derive alpha values */
        alpha_l = (det_C0_C1 == 0) ? 0.0 : det_X_C1 / det_C0_C1;
        alpha_r = (det_C0_C1 == 0) ? 0.0 : det_C0_X / det_C0_C1;

        /* If alpha negative, use the Wu/Barsky heuristic (see text) */
        /* (if alpha is 0, you get coincident control points that lead to
         * divide by zero in any subsequent NewtonRaphsonRootFind() call. */
        double segLength = d[first].distance(d[last]); //(d[first] - d[last]).Length;
        double epsilonRel = epsilon * segLength;
        if (alpha_l < epsilonRel || alpha_r < epsilonRel) {
            /* fall back on standard (probably inaccurate) formula, and subdivide further if needed. */
            double dist = segLength / 3.0;
            bezCurve[0] = new PointE(d[first]);
            bezCurve[3] = new PointE(d[last]);

            Vector2d b1Tmp=new Vector2d(tHat1); b1Tmp.scaleAdd(dist, bezCurve[0].getPoint2d());
            bezCurve[1] = new PointE(b1Tmp); //(tHat1 * dist) + bezCurve[0];
            Vector2d b2Tmp=new Vector2d(tHat2); b2Tmp.scaleAdd(dist, bezCurve[3].getPoint2d());
            bezCurve[2] = new PointE(b2Tmp); //(tHat2 * dist) + bezCurve[3];

            return (bezCurve);
        }

        /*  First and last control points of the Bezier curve are */
        /*  positioned exactly at the first and last data points */
        /*  Control points 1 and 2 are positioned an alpha distance out */
        /*  on the tangent vectors, left and right, respectively */
        bezCurve[0] = new PointE(d[first]);
        bezCurve[3] = new PointE(d[last]);
        Vector2d alphaLTmp=new Vector2d(tHat1); alphaLTmp.scaleAdd(alpha_l, bezCurve[0].getPoint2d());  
        bezCurve[1] = new PointE(alphaLTmp);    //(tHat1 * alpha_l) + bezCurve[0]
        Vector2d alphaRTmp=new Vector2d(tHat2); alphaRTmp.scaleAdd(alpha_r, bezCurve[3].getPoint2d());
        bezCurve[2] = new PointE(alphaRTmp);    //(tHat2 * alpha_r) + bezCurve[3];

        return (bezCurve);
    }

    /*
     *  Reparameterize:
     *  Given set of points and their parameterization, try to find
     *   a better parameterization.
     *
     */
    static double[] Reparameterize(Point2D[] d,int first,int last,double[] u, Point2D[] bezCurve)
    {
        int     nPts = last-first+1;    
        int     i;
        double[]    uPrime = new double[nPts];      /*  New parameter values    */

        for (i = first; i <= last; i++) {
            uPrime[i-first] = NewtonRaphsonRootFind(bezCurve, d[i], u[i-first]);
        }
        return uPrime;
    }



    /*
     *  NewtonRaphsonRootFind :
     *  Use Newton-Raphson iteration to find better root.
     */
    static double NewtonRaphsonRootFind(Point2D[] Q, Point2D P, double u)
    {
        double      numerator, denominator;
        Point2D[]     Q1 = new Point2D[3];  //Q'
        Point2D[]       Q2 = new Point2D[2];  //Q''
        Point2D       Q_u, Q1_u, Q2_u; /*u evaluated at Q, Q', & Q''  */
        double      uPrime;     /*  Improved u          */
        int         i;

        /* Compute Q(u) */
        Q_u = BezierII(3, Q, u);

        /* Generate control vertices for Q' */
        for (i = 0; i <= 2; i++) {
            double qXTmp=(Q[i+1].getX() - Q[i].getX()) * 3.0;   //Q1[i].x = (Q[i+1].x - Q[i].x) * 3.0;
            double qYTmp=(Q[i+1].getY() - Q[i].getY()) * 3.0;   //Q1[i].y = (Q[i+1].y - Q[i].y) * 3.0;
            Q1[i]=new Point2D.Double(qXTmp, qYTmp);
        }

        /* Generate control vertices for Q'' */
        for (i = 0; i <= 1; i++) {
            double qXTmp=(Q1[i+1].getX() - Q1[i].getX()) * 2.0; //Q2[i].x = (Q1[i+1].x - Q1[i].x) * 2.0;
            double qYTmp=(Q1[i+1].getY() - Q1[i].getY()) * 2.0; //Q2[i].y = (Q1[i+1].y - Q1[i].y) * 2.0;
            Q2[i]=new Point2D.Double(qXTmp, qYTmp);
        }

        /* Compute Q'(u) and Q''(u) */
        Q1_u = BezierII(2, Q1, u);
        Q2_u = BezierII(1, Q2, u);

        /* Compute f(u)/f'(u) */
        numerator = (Q_u.getX() - P.getX()) * (Q1_u.getX()) + (Q_u.getY() - P.getY()) * (Q1_u.getY());
        denominator = (Q1_u.getX()) * (Q1_u.getX()) + (Q1_u.getY()) * (Q1_u.getY()) + (Q_u.getX() - P.getX()) * (Q2_u.getX()) + (Q_u.getY() - P.getY()) * (Q2_u.getY());
        if (denominator == 0.0f) return u;

        /* u = u - f(u)/f'(u) */
        uPrime = u - (numerator/denominator);
        return (uPrime);
    }



    /*
     *  Bezier :
     *      Evaluate a Bezier curve at a particular parameter value
     * 
     */
    static Point2D BezierII(int degree, Point2D[] V, double t)
    {
        int     i, j;       
        Point2D   Q;          /* Point on curve at parameter t    */
        Point2D[]     Vtemp;      /* Local copy of control points     */

        /* Copy array   */
        Vtemp = new Point2D[degree+1];
        for (i = 0; i <= degree; i++) {
            Vtemp[i] = new Point2D.Double(V[i].getX(), V[i].getY());
        }

        /* Triangle computation */
        for (i = 1; i <= degree; i++) { 
            for (j = 0; j <= degree-i; j++) {
                double tmpX, tmpY;
                tmpX = (1.0 - t) * Vtemp[j].getX() + t * Vtemp[j+1].getX();
                tmpY = (1.0 - t) * Vtemp[j].getY() + t * Vtemp[j+1].getY();
                Vtemp[j].setLocation(tmpX, tmpY);
            }
        }

        Q = Vtemp[0];
        return Q;
    }


    /*
     *  B0, B1, B2, B3 :
     *  Bezier multipliers
     */
    static double B0(double u)
    {
        double tmp = 1.0 - u;
        return (tmp * tmp * tmp);
    }


    static double B1(double u)
    {
        double tmp = 1.0 - u;
        return (3 * u * (tmp * tmp));
    }

    static double B2(double u)
    {
        double tmp = 1.0 - u;
        return (3 * u * u * tmp);
    }

    static double B3(double u)
    {
        return (u * u * u);
    }


    /*
     * ComputeLeftTangent, ComputeRightTangent, ComputeCenterTangent :
     *Approximate unit tangents at endpoints and "center" of digitized curve
     */
    static Vector2d ComputeLeftTangent(Point[] d, int end)
    {
        Vector2d  tHat1=new Vector2d(PointE.getPoint2d(d[end+1]));
        tHat1.sub(PointE.getPoint2d(d[end]));
        tHat1.normalize();
        return tHat1;
    }

    static Vector2d ComputeRightTangent(Point[] d, int end)
    {
        //tHat2 = V2SubII(d[end-1], d[end]); tHat2 = *V2Normalize(&tHat2);
        Vector2d  tHat2=new Vector2d(PointE.getPoint2d(d[end-1]));
        tHat2.sub(PointE.getPoint2d(d[end]));
        tHat2.normalize();
        return tHat2;
    }

    static Vector2d ComputeCenterTangent(Point[] d ,int center)
    {
        //V1 = V2SubII(d[center-1], d[center]);
        Vector2d  V1=new Vector2d(PointE.getPoint2d(d[center-1]));
        V1.sub(new PointE(d[center]).getPoint2d());

        //V2 = V2SubII(d[center], d[center+1]);
        Vector2d  V2=new Vector2d(PointE.getPoint2d(d[center]));
        V2.sub(PointE.getPoint2d(d[center+1]));

        //tHatCenter.x = (V1.x + V2.x)/2.0;
        //tHatCenter.y = (V1.y + V2.y)/2.0;
        //tHatCenter = *V2Normalize(&tHatCenter);
        Vector2d tHatCenter=new Vector2d((V1.x + V2.x)/2.0, (V1.y + V2.y)/2.0);
        tHatCenter.normalize();
        return tHatCenter;
    }

    /*
     *  ChordLengthParameterize :
     *  Assign parameter values to digitized points 
     *  using relative distances between points.
     */
    static double[] ChordLengthParameterize(Point[] d,int first,int last)
    {
        int     i;  
        double[]    u = new double[last-first+1];           /*  Parameterization        */

        u[0] = 0.0;
        for (i = first+1; i <= last; i++) {
            u[i-first] = u[i-first-1] + d[i-1].distance(d[i]);
        }

        for (i = first + 1; i <= last; i++) {
            u[i-first] = u[i-first] / u[last-first];
        }

        return u;
    }




    /*
     *  ComputeMaxError :
     *  Find the maximum squared distance of digitized points
     *  to fitted curve.
    */
    static double ComputeMaxError(Point2D[] d, int first, int last, Point2D[] bezCurve, double[] u, AtomicInteger splitPoint)
    {
        int     i;
        double  maxDist;        /*  Maximum error       */
        double  dist;       /*  Current error       */
        Point2D   P;          /*  Point on curve      */
        Vector2d  v;          /*  Vector from point to curve  */

        int tmpSplitPoint=(last - first + 1)/2;
        maxDist = 0.0;

        for (i = first + 1; i < last; i++) {                
            P = BezierII(3, bezCurve, u[i-first]);

            v = new Vector2d(P.getX() - d[i].getX(), P.getY() - d[i].getY());   //P - d[i];
            dist = v.lengthSquared();
            if (dist >= maxDist) {
                maxDist = dist;
                tmpSplitPoint=i;
            }
        }
        splitPoint.set(tmpSplitPoint);
        return maxDist;
    }







    /**
     * This is kind of a bridge between javax.vecmath and java.util.Point2D
     * @author Ruben
     * @since 1.24
     */
    public static class PointE extends Point2D.Double {
        private static final long serialVersionUID = -1482403817370130793L;
        public PointE(Tuple2d tup) {
            super(tup.x, tup.y);
        }
        public PointE(Point2D p) {
            super(p.getX(), p.getY());
        }
        public PointE(double x, double y) {
            super(x, y);
        }
        public PointE scale(double dist) {
            return new PointE(getX()*dist, getY()*dist);
        }
        public PointE scaleAdd(double dist, Point2D sum) {
            return new PointE(getX()*dist + sum.getX(), getY()*dist + sum.getY());
        }
        public PointE substract(Point2D p) {
            return new PointE(getX() - p.getX(), getY() - p.getY());
        }
        public Point2d getPoint2d() {
            return getPoint2d(this);
        }
        public static Point2d getPoint2d(Point2D p) {
            return new Point2d(p.getX(), p.getY());
        }
    }

Voici une image de ce dernier travail, blanc sont des lignes, et rouge sont Bézier:

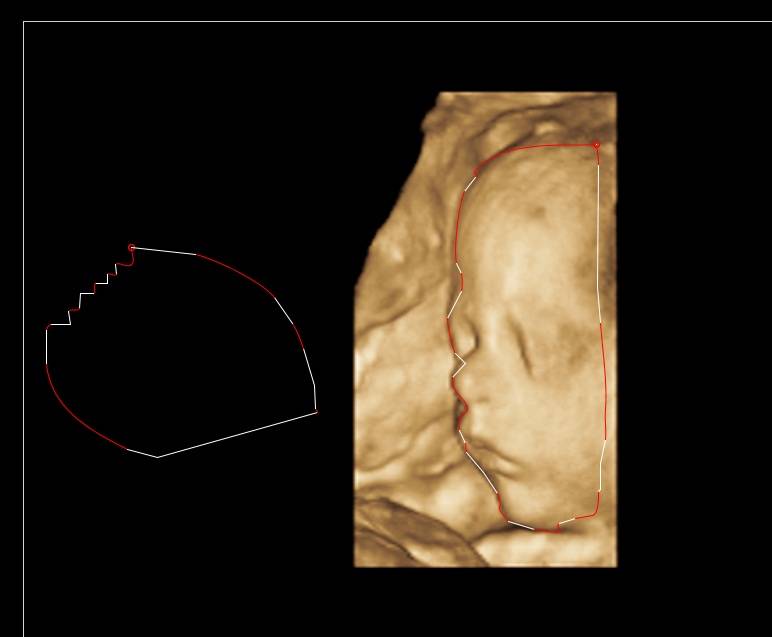
En utilisant cette approche, nous utilisons moins de points de contrôle et plus précis. La sensibilité de la création de lignes peut être ajustée via l'attribut lineSensitivity. Si vous ne voulez pas que les lignes soient utilisées du tout, définissez-les sur infinite.

Je suis sûr que cela peut être amélioré. N'hésitez pas à contribuer :)

L'algorithme ne fait aucune réduction, et à cause de la première explication dans mon post, nous devons en exécuter un. Voici une implémentation DouglasPeuckerReduction, qui pour moi fonctionne dans certains cas encore plus efficacement (moins de points à stocker et plus rapide à rendre) qu'un FitCurves supplémentaire

import java.awt.Point;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;


public class DouglasPeuckerReduction {

    public static List<Point> reduce(Point[] points, double tolerance)
    {
        if (points == null || points.length < 3) return Arrays.asList(points);

        int firstPoint = 0;
        int lastPoint = points.length - 1;

        SortedList<Integer> pointIndexsToKeep;
        try {
            pointIndexsToKeep = new SortedList<Integer>(LinkedList.class);
        } catch (Throwable t) {
            t.printStackTrace(System.out);
            ErrorReport.process(t);
            return null;
        }

        //Add the first and last index to the keepers
        pointIndexsToKeep.add(firstPoint);
        pointIndexsToKeep.add(lastPoint);

        //The first and the last point cannot be the same
        while (points[firstPoint].equals(points[lastPoint])) {
            lastPoint--;
        }

        reduce(points, firstPoint, lastPoint, tolerance, pointIndexsToKeep);

        List<Point> returnPoints = new ArrayList<Point>(pointIndexsToKeep.size());

        for (int pIndex : pointIndexsToKeep) {
             returnPoints.add(points[pIndex]);
        }

        return returnPoints;
    }


    private static void reduce(Point[] points, int firstPoint, int lastPoint, double tolerance, List<Integer> pointIndexsToKeep) {
        double maxDistance = 0;
        int indexFarthest = 0;

        Line tmpLine=new Line(points[firstPoint], points[lastPoint]);

        for (int index = firstPoint; index < lastPoint; index++) {
            double distance = tmpLine.getDistanceFrom(points[index]);
            if (distance > maxDistance) {
                maxDistance = distance;
                indexFarthest = index;
            }
        }

        if (maxDistance > tolerance && indexFarthest != 0) {
            //Add the largest point that exceeds the tolerance
            pointIndexsToKeep.add(indexFarthest);

            reduce(points, firstPoint, indexFarthest, tolerance, pointIndexsToKeep);
            reduce(points, indexFarthest, lastPoint, tolerance, pointIndexsToKeep);
        }
    }

}

J'utilise ici ma propre implémentation D'une SortedList, et d'une ligne. Vous devrez le faire vous-même, désolé.

Je ne l'ai pas testé, mais une approche qui vient à l'esprit serait d'échantillonner des valeurs dans un intervalle et de créer une spline pour relier les points.

Par exemple, disons que la valeur x de votre courbe commence à 0 et se termine à 10. Donc, vous échantillonnez les valeurs y à x = 1,2,3,4,5,6,7,8,9,10 et créez une spline à partir des points (0, y(0)), (1,y(1)), ... (10, y(10))

Il aurait probablement des problèmes tels que des pointes accidentelles dessinées par l'utilisateur, mais cela peut valoir le coup

Pour les utilisateurs Silverlight de la réponse de Kris, le Point est bloqué et le vecteur n'existe pas. C'est une classe vectorielle minimale qui prend en charge le code:

public class Vector
{
   public double X { get; set; }
   public double Y { get; set; }
   public Vector(double x=0, double y=0)
   {
      X = x;
      Y = y;
   }

   public static implicit operator Vector(Point b)
   {
      return new Vector(b.X, b.Y);
   }

   public static Point operator *(Vector left, double right)
   {
      return new Point(left.X * right, left.Y * right);
   }
   public static Vector operator -(Vector left, Point right)
   {
      return new Vector(left.X - right.X, left.Y - right.Y);
   }

   internal void Negate()
   {
      X = -X;
      Y = -Y;
   }

   internal void Normalize()
   {
      double factor = 1.0 / Math.Sqrt(LengthSquared);
      X *= factor;
      Y *= factor;
   }

   public double LengthSquared { get { return X * X + Y * Y; } }
}

Devait également aborder l'utilisation des opérateurs Length et+, -. J'ai choisi d'ajouter simplement des fonctions à la classe FitCurves, et de réécrire leurs usages où le compilateur s'est plaint.

  public static double Length(Point a, Point b)
  {
     double x = a.X-b.X;
     double y = a.Y-b.Y;
     return Math.Sqrt(x*x+y*y);
  }

  public static Point Add(Point a, Point b)
  {
     return new Point(a.X + b.X, a.Y + b.Y);
  }

  public static Point Subtract(Point a, Point b)
  {
     return new Point(a.X - b.X, a.Y - b.Y);
  }