Polygones simplifiés (ou lisses) contenant le polygone détaillé original

Modifier

depuis 2013, la plupart des liens ci-dessous ne sont plus fonctionnels. Cependant, j'ai trouvé le papier Cité, algorithme inclus, encore disponible sur ce serveur (très lent) .

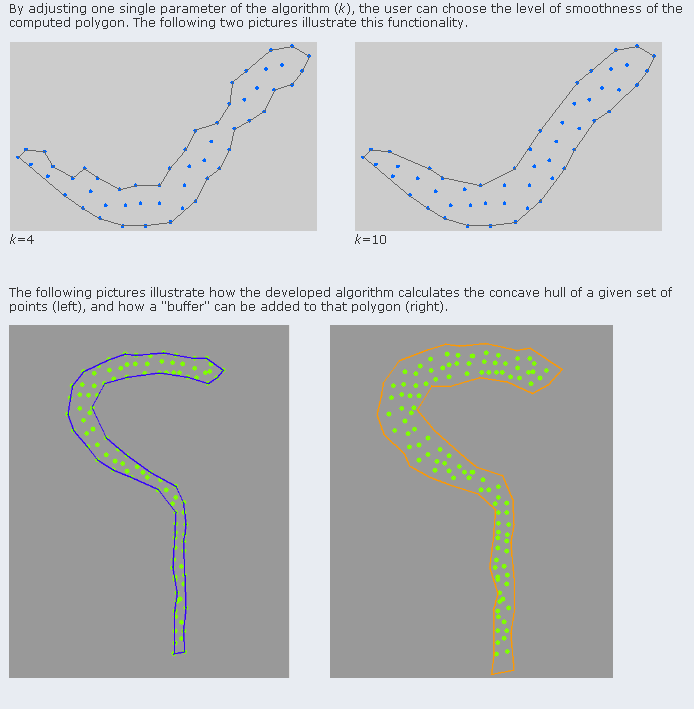
ici vous pouvez trouver un projet traitant exactement de vos problèmes. Bien qu'il travaille principalement avec une zone "rempli" par des points, vous pouvez réglez - le pour qu'il fonctionne avec une définition de type "périmètre" comme le vôtre.

il utilise une approche de K-voisins les plus proches pour calculer la région.

Exemples:

ici vous pouvez demander une copie du papier.

apparemment ils prévu d'offrir un service pour demander des calculs, mais je ne l'ai pas testé, et probablement il ne fonctionne pas.

HTH!

C'est un problème intéressant! Je n'ai jamais essayé quelque chose comme ça, mais j'ai une idée en tête... toutes mes excuses si il n'a pas de sens ou ne fonctionne pas :)

1. calculez une coque convexe, qui pourrait être beaucoup trop grande /imprécise
2. diviser la coque en n tranches, par exemple joindre chacun des sommets de la coque au centre
3. calculez l'intersection de votre objet avec chaque tranche
4. répéter de façon récursive pour chaque intersection (calcul de la coque de l'intersection, etc.)

chaque niveau de récursion devrait donner une meilleure approximation.... lorsque vous avez atteint un niveau satisfaisant, fusionnez toutes les coques de ce niveau pour obtenir le polygone final.

est-ce que ça pourrait faire l'affaire?

j'ai eu un problème très similaire : j'avais besoin d'une simplification gonflante des polygones.

j'ai fait un algorithme simple, en enlevant le point concav (ce qui augmentera la taille du polygone) ou en enlevant le bord convexe (entre 2 points convexes) et en prolongeant les bords adjacents. Dans tous les cas, faire l'une de ces deux possibilités supprimera un point sur le polygone.

j'ai choisi d'enlever le point ou le bord qui conduit à la plus petite variation de surface. Vous pouvez répétez ce processus, jusqu'à ce que la simplification soit acceptable pour vous (par exemple pas plus de 200 points).

les 2 principales difficultés ont été d'obtenir un algorithme rapide (en évitant de calculer deux fois la variation de l'écartement des contours/arêtes et en maintenant les possibilités triées) et d'éviter d'insérer une auto-intersection dans le processus (pas très facile à faire et à expliquer, mais possible avec une complexité computationnelle limitée).

En fait, après avoir regardé de plus près, il est un idée similaire à celle de Visvalingam avec adaptation pour l'enlèvement de bord.

dans une certaine mesure, Je ne suis pas sûr de ce que vous essayez de faire, mais il semble que vous avez deux très bonnes réponses. L'un est Ramer–Douglas–Peucker (DP) et l'autre calcule la forme alpha (également appelé une coque Concave, coque non convexe, etc.). J'ai trouvé un article plus récent décrivant des formes alpha et je l'ai relié ci-dessous.

personnellement, je pense que DP avec extension polygon est la voie à suivre. Je ne sais pas pourquoi vous pensez que ça ne réduira pas considérablement le nombre de Sommets. Avec DP vous fournissez un facteur et vous pouvez faire tout ce que vous voulez au point où vous vous retrouvez avec un triangle n'importe ce que votre entrée. Choisir ce facteur peut être difficile, mais dans votre cas, je pense que c'est la meilleure méthode. Vous devriez être en mesure de déterminer le facteur en fonction de la taille du plus grand morceau de détail que vous voulez passer. Vous pouvez le faire avec des tests directs ou en le calculant à partir de vos données source.

http://www.it.uu.se/edu/course/homepage/projektTDB/ht13/project10/Project-10-report.pdf

je pense l'algorithme de Visvalingam peut être adapté à cet effet - en sautant l'enlèvement des triangles qui réduiraient la zone.