régression sigmoïde avec scipy, numpy, python, etc.

en utilisant scipy.optimiser.leastsq:

import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize

def sigmoid(p,x):
    x0,y0,c,k=p
    y = c / (1 + np.exp(-k*(x-x0))) + y0
    return y

def residuals(p,x,y):
    return y - sigmoid(p,x)

def resize(arr,lower=0.0,upper=1.0):
    arr=arr.copy()
    if lower>upper: lower,upper=upper,lower
    arr -= arr.min()
    arr *= (upper-lower)/arr.max()
    arr += lower
    return arr

# raw data
x = np.array([821,576,473,377,326],dtype='float')
y = np.array([255,235,208,166,157],dtype='float')

x=resize(-x,lower=0.3)
y=resize(y,lower=0.3)
print(x)
print(y)
p_guess=(np.median(x),np.median(y),1.0,1.0)
p, cov, infodict, mesg, ier = scipy.optimize.leastsq(
    residuals,p_guess,args=(x,y),full_output=1,warning=True)  

x0,y0,c,k=p
print('''\
x0 = {x0}
y0 = {y0}
c = {c}
k = {k}
'''.format(x0=x0,y0=y0,c=c,k=k))

xp = np.linspace(0, 1.1, 1500)
pxp=sigmoid(p,xp)

# Plot the results
plt.plot(x, y, '.', xp, pxp, '-')
plt.xlabel('x')
plt.ylabel('y',rotation='horizontal') 
plt.grid(True)
plt.show()

les rendements

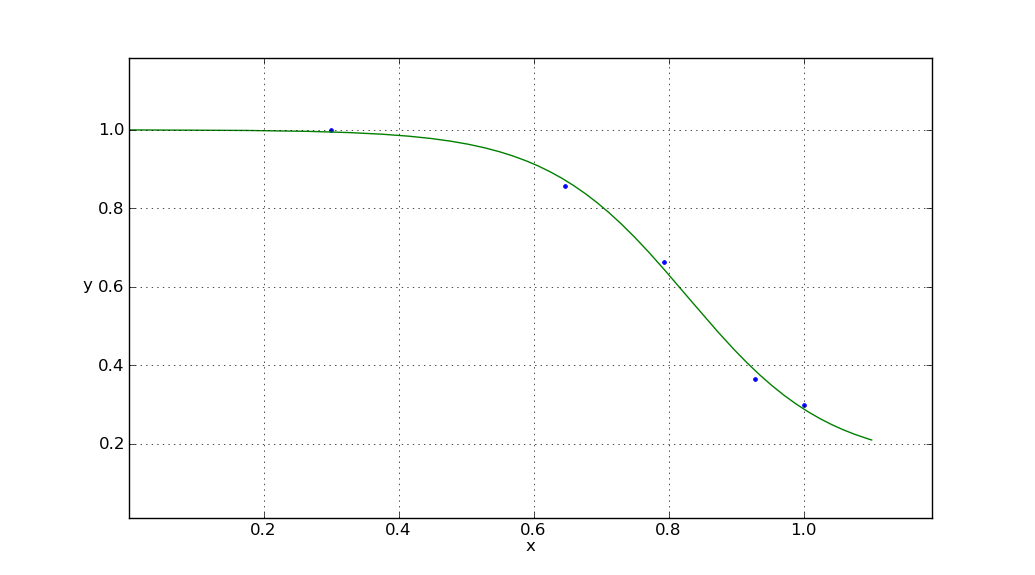
avec des paramètres sigmoïdes

x0 = 0.826964424481
y0 = 0.151506745435
c = 0.848564826467
k = -9.54442292022

notez que pour les versions plus récentes de scipy (par exemple 0.9) il y a aussi le scipy.optimiser.curve_fit fonction plus facile à utiliser que leastsq. Une discussion pertinente sur l'ajustement des sigmoïdes à l'aide de curve_fit peut être trouvé ici.

Edit: A resize la fonction a été ajoutée pour que les données brutes puissent être rééchelonnées et déplacées pour s'adapter à n'importe quelle boîte de limite désirée.

---

"votre nom semble pop up comme un écrivain de la documentation de scipy"

avertissement: Je ne suis pas un rédacteur de documentation scipy. Je suis juste un utilisateur, et un novice. Beaucoup de ce que je connais leastsq vient de la lecture ce tutoriel, écrit par Travis Oliphant.

1.) Faire leastsq() appel de résidus(), qui renvoie alors la différence entre le vecteur d'entrée y et le vecteur vecteur y retourné par le sigmoïde() la fonction?

Oui! exactement.

si c'est le cas, comment tient-il compte de la différence dans la longueur de l'entrée le vecteur y et le vecteur y sont retournés par le sigmoïde() la fonction?

Les longueurs sont identiques:

In [138]: x
Out[138]: array([821, 576, 473, 377, 326])

In [139]: y
Out[139]: array([255, 235, 208, 166, 157])

In [140]: p=(600,200,100,0.01)

In [141]: sigmoid(p,x)
Out[141]: 
array([ 290.11439268,  244.02863507,  221.92572521,  209.7088641 ,
        206.06539033])

une des choses merveilleuses à propos de Numpy est qu'il permet d'écrire des équations "vectorielles" qui fonctionnent sur des tableaux entiers.

y = c / (1 + np.exp(-k*(x-x0))) + y0

pourrait ressembler à cela fonctionne sur les flotteurs (en effet il le ferait) mais si vous faites x un tableau numpy, et c,k,x0,y0 flotteurs, alors l'équation définit y pour être un tableau numpy de la même forme que x. Donc sigmoid(p,x) renvoie un numpy array. Il y a une explication plus complète de la façon dont cela fonctionne dans le nummpybook (lecture requise pour les utilisateurs sérieux de numpy).

2.) Il semble que je puisse appeler leastsq () pour n'importe quelle équation mathématique, aussi longtemps que je accéder à cette équation mathématique au moyen d'un les fonctions résiduelles, qui à leur tour appelle la fonction mathématique. Est-ce vrai?

Vrai. leastsq tente de minimiser la somme des carrés des résidus (les différences). Il recherche le paramètre-espace (toutes les valeurs possibles de p) à la recherche de l' p qui minimise cette somme de carrés. x et y envoi residuals, sont vos données brutes. Ils sont fixes. Ils ne changent pas. C'est le ps (les paramètres de la fonction sigmoïde)leastsq tente de minimiser.

3.) De plus, je remarque que p_guess a le même nombre d'éléments que P. Does cela signifie que les quatre éléments de p_guess correspond dans l'ordre, respectivement, avec les valeurs retournées par x0, y0, c, et k?

Exactement! Comme la méthode de Newton,leastsq besoins une première supposition pour p. Vous fournir en tant que p_guess. Quand vous voyez

scipy.optimize.leastsq(residuals,p_guess,args=(x,y))

vous pouvez penser que dans le cadre de l'algorithme de leastsq (en fait l'algorithme de Levenburg-Marquardt) comme premier passage, leastsq appelle residuals(p_guess,x,y). Remarquez la similitude visuelle entre

(residuals,p_guess,args=(x,y))

et

residuals(p_guess,x,y)

Il peut vous aider à vous souvenir de l'ordre et le sens de l'argumentation leastsq.

residuals, comme sigmoid renvoie un numpy array. Valeur dans le tableau sont au carré, puis additionnées. C'est le nombre de battre. p_guess est alors varié comme leastsq regarde pour un ensemble de valeurs qui minimise residuals(p_guess,x,y).

4.) Est le p qui est envoyé comme argument aux résidus () et sigmoid() fonctionne avec le même p que sera produit par leastsq (), et le la fonction leastsq() utilise ce p en interne avant de le retourner?

eh Bien, pas exactement. Comme vous le savez maintenant, p_guess est varié comme leastsq recherche p valeur qui minimise residuals(p,x,y). p (re, p_guess) envoyé à leastsq a la même forme que l' p qui est retournée par leastsq. Évidemment, les valeurs devraient être différentes sauf si vous êtes un enfer d'une devinette :)

5.) P et p_guess peuvent avoir n'importe quel nombre d'éléments, selon le la complexité de l'équation utilisée comme un modèle, tant que le nombre de les éléments de p est égal au nombre des éléments en p_guess?

Oui. Je n'ai pas un test de contrainte leastsq pour un très grand nombre de paramètres, mais c'est un outil extrêmement puissant.

je ne pense pas que vous allez obtenir de bons résultats avec une approximation polynomiale de degré -- depuis tous les polynômes vont à l'infini pour un X suffisamment grand et petit, mais une courbe sigmoïde approchera asymptotiquement une valeur finie dans chaque direction.

Je ne suis pas un programmeur Python, donc je ne sais pas si numpy a un ajustement de courbe plus général routine. Si vous devez rouler votre propre, peut-être cet article sur régression Logistique vous donnera quelques idées.

Pour la régression logistique en Python, le scikits-apprendre expose le code de raccord haute performance:

http://scikit-learn.sourceforge.net/modules/linear_model.html#logistic-regression

scipy offre scipy.optimiser.curve_fit qui possèdent un appel moins compliqué. Si quelqu'un veut une version rapide de comment le même processus ressemblerait dans ces termes je présente un exemple minimal ci-dessous:

def sigmoid(x, k, x0):

    return 1.0 / (1 + np.exp(-k * (x - x0)))

# Parameters of the true function
n_samples = 1000
true_x0 = 15
true_k = 1.5
sigma = 0.2

# Build the true function and add some noise
x = np.linspace(0, 30, num=n_samples)
y = sigmoid(x, k=true_k, x0=true_x0) 
y_with_noise = y + sigma * np.random.randn(n_samples)

# Sample the data from the real function (this will be your data)
some_points = np.random.choice(1000, size=30)  # take 30 data points
xdata = x[some_points]
ydata = y_with_noise[some_points]

# Fit the curve
popt, pcov = curve_fit(return_sigmoid, xdata, ydata)
estimated_k, estimated_x0 = popt

# Plot the fitted curve
y_fitted = sigmoid(x, k=estimated_k, x0=estimated_x0)

# Plot everything for illustration
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y_fitted, '--', label='fitted')
ax.plot(x, y, '-', label='true')
ax.plot(xdata, ydata, 'o', label='samples')

ax.legend()

Le résultat de ceci est montré dans la figure suivante: