Voir si les données sont normalement distribuées en R
quelqu'un peut-il s'il vous plaît m'aider à remplir la fonction suivante dans R:
#data is a single vector of decimal values
normally.distributed <- function(data) {
if(data is normal)
return(TRUE)
else
return(NO)
}
8 réponses
les tests de normalité ne font pas ce que la plupart pensent qu'ils font. Le test de Shapiro, Anderson Darling, et d'autres sont des tests d'hypothèse nuls contre l'hypothèse de la normalité. Ceux-ci ne devraient pas être utilisés pour déterminer s'il convient d'utiliser des procédures statistiques de la théorie normale. En fait, ils sont pratiquement sans valeur pour l'analyste de données. Dans quelles conditions sommes-nous intéressés à rejeter l'hypothèse nulle que les données sont distribuées normalement? Je n'ai jamais rencontré une situation où un test normal est la bonne chose à faire. Lorsque la taille de l'échantillon est petite, même de grands écarts par rapport à la normalité ne sont pas détectés, et lorsque la taille de votre échantillon est grande, même le plus petit écart par rapport à la normalité conduira à un null rejeté.
par exemple:
> set.seed(100)
> x <- rbinom(15,5,.6)
> shapiro.test(x)
Shapiro-Wilk normality test
data: x
W = 0.8816, p-value = 0.0502
> x <- rlnorm(20,0,.4)
> shapiro.test(x)
Shapiro-Wilk normality test
data: x
W = 0.9405, p-value = 0.2453
ainsi, dans ces deux cas (variations binomiales et lognormales) la valeur p est > 0,05 provoquant un échec de rejeter le nul (que les données sont normales). Cela signifie-t-il que nous devons conclure que les données sont normal? (indice: la réponse est non). Ne pas rejeter n'est pas la même chose que d'accepter. C'est le test d'hypothèse 101.
mais qu'en est-il des échantillons de plus grande taille? Prenons le cas où la distribution est très presque normale.
> library(nortest)
> x <- rt(500000,200)
> ad.test(x)
Anderson-Darling normality test
data: x
A = 1.1003, p-value = 0.006975
> qqnorm(x)
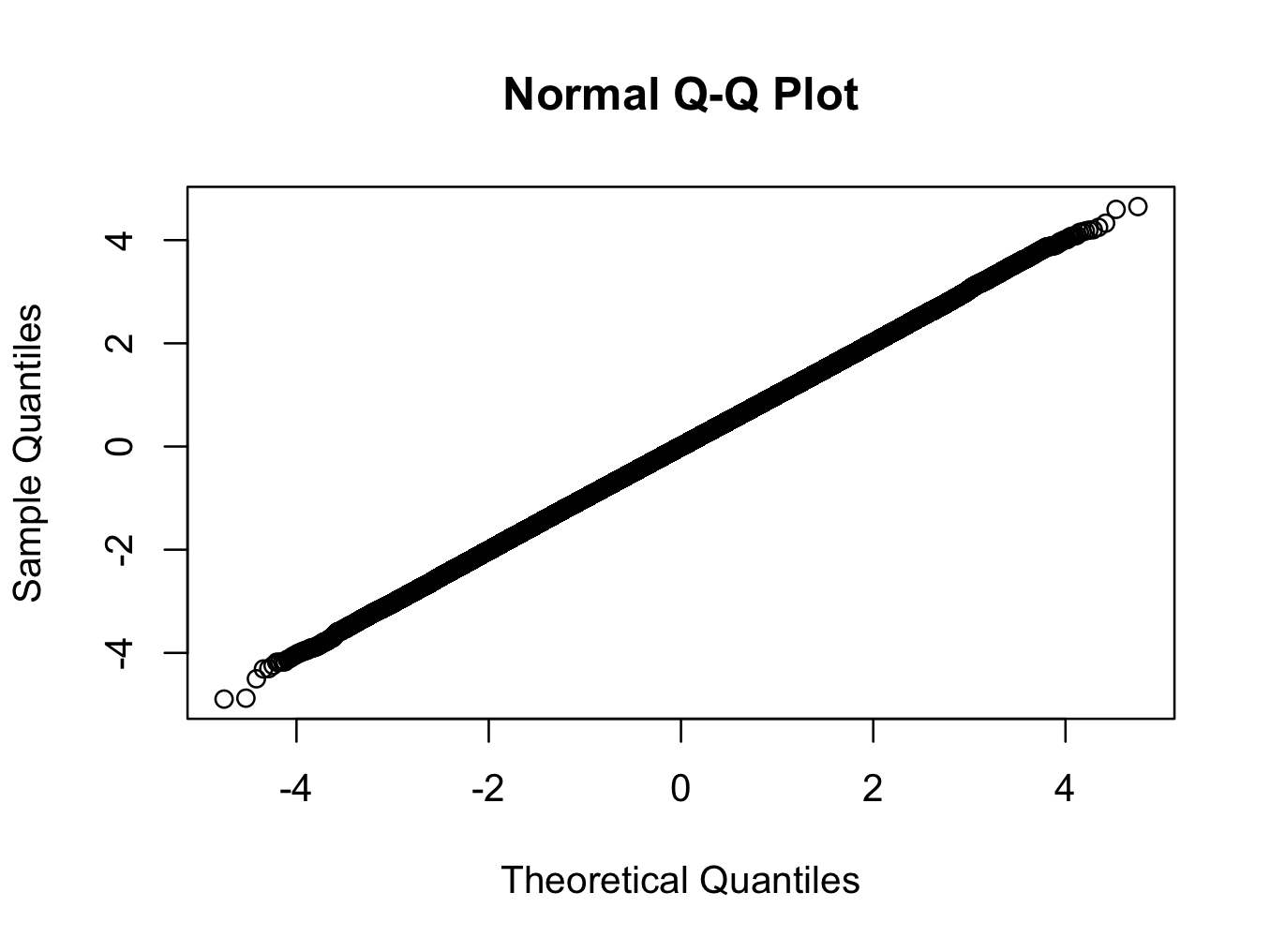
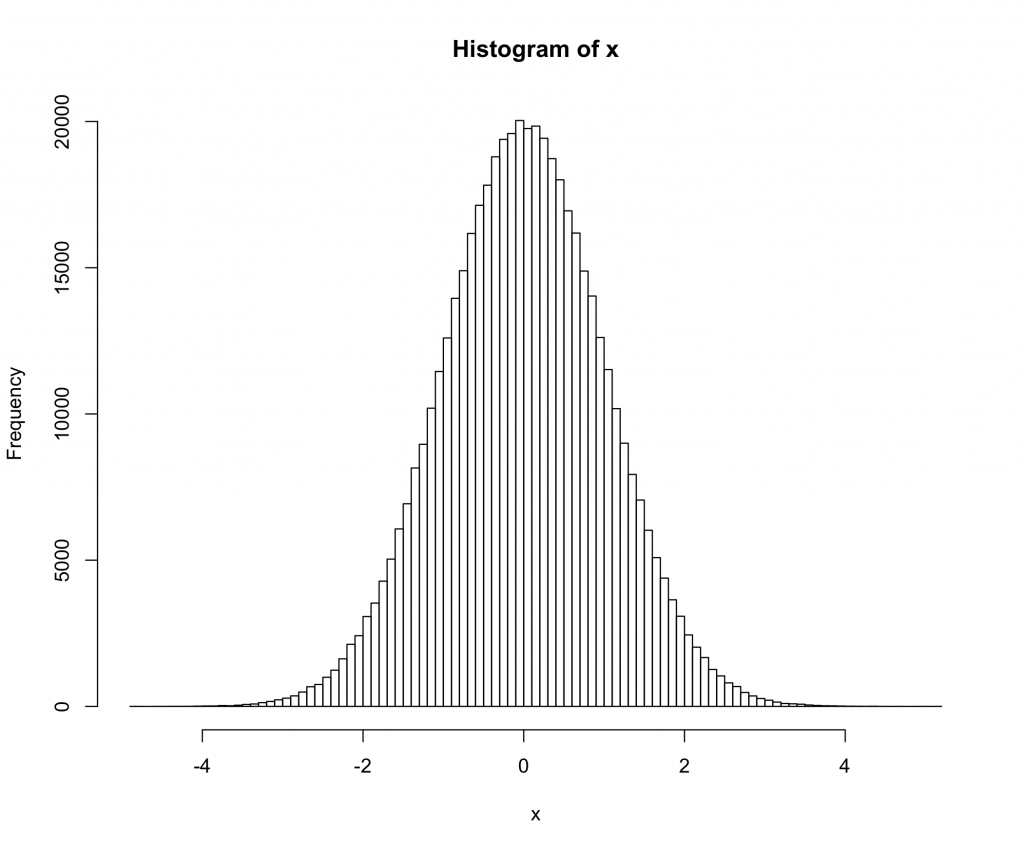
ici nous utilisons une distribution t avec 200 degrés de liberté. Le graphique qq montre la distribution est plus proche de la normale que toute autre distribution que vous êtes susceptible de voir dans le monde réel, mais le test rejette la normalité avec un très haut degré de confiance.
est-ce que le test significatif contre la normalité signifie que nous ne devrions pas utiliser les statistiques de la théorie normale dans ce cas? (un autre indice: la réponse est non :) )
je recommande fortement le SnowsPenultimateNormalityTest dans le paquet TeachingDemos . La documentation de la fonction vous est bien plus utile que le test lui-même. Lire attentivement avant d'utiliser le test.
SnowsPenultimateNormalityTest a certainement ses vertus, mais vous pouvez également regarder qqnorm .
X <- rlnorm(100)
qqnorm(X)
qqnorm(rnorm(100))
envisager d'utiliser la fonction shapiro.test , qui effectue le test de Shapiro-Wilks pour la normalité. J'ai été heureux avec elle.
de la bibliothèque(DnE)
x < - rnorm (1000,0,1)
est.norm (x,10,0.05)
le test Anderson-Darling est également utile.
library(nortest)
ad.test(data)
lorsque vous effectuez un test, avez-vous jamais probabilty de rejeter l'hypothèse nulle lorsqu'elle est vraie.
voir le code suivant:
p=function(n){
x=rnorm(n,0,1)
s=shapiro.test(x)
s$p.value
}
rep1=replicate(1000,p(5))
rep2=replicate(1000,p(100))
plot(density(rep1))
lines(density(rep2),col="blue")
abline(v=0.05,lty=3)
le graphique montre que si vous avez une taille d'échantillon petite ou grande a 5% des fois où vous avez une chance de rejeter l'hypothèse nulle quand elle est vraie (une erreur de Type I)
en plus de qqplots et de L'essai Shapiro-Wilk, les méthodes suivantes peuvent être utiles.
Qualitative:
- histogramme comparé à la normale
- cdf par rapport à la normale
- graphe de densité GG
- ggqqplot
Quantitative:
les méthodes qualitives peuvent être produites en utilisant ce qui suit dans R:
library("ggpubr")
library("car")
h <- hist(data, breaks = 10, density = 10, col = "darkgray")
xfit <- seq(min(data), max(data), length = 40)
yfit <- dnorm(xfit, mean = mean(data), sd = sd(data))
yfit <- yfit * diff(h$mids[1:2]) * length(data)
lines(xfit, yfit, col = "black", lwd = 2)
plot(ecdf(data), main="CDF")
lines(ecdf(rnorm(10000)),col="red")
ggdensity(data)
ggqqplot(data)
un mot de mise en garde - Ne pas appliquer aveuglément les tests. Une bonne compréhension des statistiques vous aidera à comprendre quand utiliser les tests et l'importance des hypothèses dans la vérification des hypothèses.