Échantillonnage points aléatoires uniformément répartis à l'intérieur d'un volume sphérique
je cherche à être en mesure de générer un échantillon aléatoire uniforme des emplacements de particules qui tombent dans un volume sphérique.
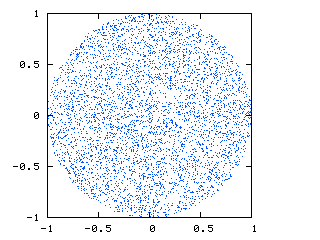
l'image ci-dessous (courtoisie de http://nojhan.free.fr/metah / ) montre ce que je cherche. C'est une tranche à travers la sphère, montrant une répartition uniforme des points:
C'est ce que je reçois actuellement:
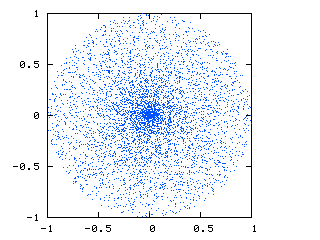
vous pouvez voir qu'il y a un amas de points au centre dû à la conversion entre les coordonnées sphériques et cartésiennes.
le code que j'utilise est:
def new_positions_spherical_coordinates(self):
radius = numpy.random.uniform(0.0,1.0, (self.number_of_particles,1))
theta = numpy.random.uniform(0.,1.,(self.number_of_particles,1))*pi
phi = numpy.arccos(1-2*numpy.random.uniform(0.0,1.,(self.number_of_particles,1)))
x = radius * numpy.sin( theta ) * numpy.cos( phi )
y = radius * numpy.sin( theta ) * numpy.sin( phi )
z = radius * numpy.cos( theta )
return (x,y,z)
ci-dessous est un code MATLAB qui est censé créer un échantillon sphérique uniforme, qui est similaire à l'équation donnée par http://nojhan.free.fr/metah . Je n'arrive pas à le déchiffrer ou comprendre ce qu'ils ont fait.
function X = randsphere(m,n,r)
% This function returns an m by n array, X, in which
% each of the m rows has the n Cartesian coordinates
% of a random point uniformly-distributed over the
% interior of an n-dimensional hypersphere with
% radius r and center at the origin. The function
% 'randn' is initially used to generate m sets of n
% random variables with independent multivariate
% normal distribution, with mean 0 and variance 1.
% Then the incomplete gamma function, 'gammainc',
% is used to map these points radially to fit in the
% hypersphere of finite radius r with a uniform % spatial distribution.
% Roger Stafford - 12/23/05
X = randn(m,n);
s2 = sum(X.^2,2);
X = X.*repmat(r*(gammainc(s2/2,n/2).^(1/n))./sqrt(s2),1,n);
j'apprécierais beaucoup toute suggestion sur la génération d'un échantillon vraiment uniforme à partir d'un volume sphérique en Python.
il semble y avoir beaucoup d'exemples montrant comment échantillonner à partir d'une coquille Sphérique uniforme, mais cela semble être plus facile un problème plus facile. Le problème a trait à l'échelle - il devrait y avoir moins de particules dans un rayon de 0,1 que dans un rayon de 1,0 pour produire un échantillon uniforme à partir de le volume de la sphère.
" Edit: fixe et supprime le fait que j'ai demandé normalement et je voulais dire uniforme.
8 réponses
alors que je préfère la méthode de rejet pour les sphères, pour l'exhaustivité j'offre la solution exacte .
en coordonnées sphériques, compte tenu de la règle d'échantillonnage :
phi = random(0,2pi)
costheta = random(-1,1)
u = random(0,1)
theta = arccos( costheta )
r = R * cuberoot( u )
maintenant vous avez un (r, theta, phi) groupe qui peut être transformé en (x, y, z) de la manière habituelle
x = r * sin( theta) * cos( phi )
y = r * sin( theta) * sin( phi )
z = r * cos( theta )
génère un ensemble de points uniformément répartis dans un cube, puis écarte ceux dont la distance du centre dépasse le rayon de la sphère désirée.
il y a une façon brillante de générer uniformément des points sur la sphère dans l'espace n-dimensionnel, et vous l'avez pointé dans votre question (je veux dire code MATLAB).
pourquoi ça marche? La réponse est: regardons la densité de probabilité de la distribution normale n-dimensionnelle. Il est égal à (constants)
exp(-x_1*x_1/2) *exp (- x_2*x_2/2)... = exp (- r*r / 2), donc, cela ne dépend pas de la direction, seulement sur la distance! Cela signifie, d'après vous normaliser vecteur, la densité de la distribution résultante sera constante à travers la sphère.
cette méthode doit certainement être préférée en raison de sa simplicité, la généralité et l'efficacité (et la beauté). Le code, qui génère 1000 événements sur la sphère en trois dimensions:
size = 1000
n = 3 # or any positive integer
x = numpy.random.normal(size=(size, n))
x /= numpy.linalg.norm(x, axis=1)[:, numpy.newaxis]
BTW, le bon lien à regarder: http://www-alg.ist.hokudai.ac.jp/ ~ jan / randsphere.pdf
comme pour avoir une distribution uniforme dans une sphère, au lieu de normaliser un vecteur, vous devriez multiplier vercor par quelque f (r): f (r) * r est distribué avec une densité proportionnelle à r^n sur [0,1], ce qui a été fait dans le code que vous avez publié
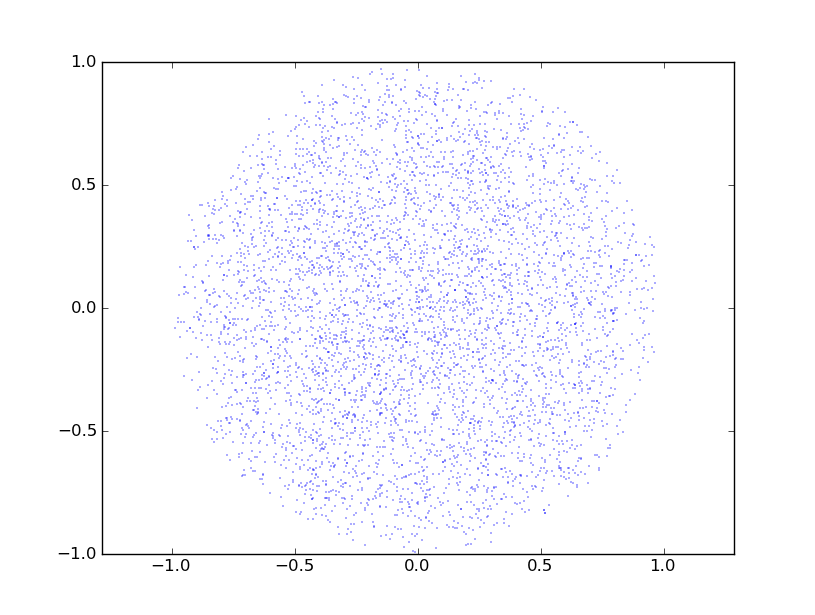
est-ce assez uniforme pour vos besoins?
In []: p= 2* rand(3, 1e4)- 1
In []: p= p[:, sum(p* p, 0)** .5<= 1]
In []: p.shape
Out[]: (3, 5216)
une tranche de celui-ci
In []: plot(p[0], p[2], '.')
ressemble à:
le vecteur tridimensionnel gaussien normé est uniformément distribué sur la sphère, voir http://mathworld.wolfram.com/SpherePointPicking.html
par exemple:
N = 1000
v = numpy.random.uniform(size=(3,N))
vn = v / numpy.sqrt(numpy.sum(v**2, 0))
Je suis D'accord avec Alleo. J'ai traduit votre code Matlab en Python et il peut générer des milliers de points très rapidement (une fraction de seconde dans mon ordinateur pour la 2D et la 3D). Je l'ai même testé sur des hypersphères 5D. J'ai trouvé votre code si utile que je postule dans une étude. Tim McJilton, qui dois-je ajouter comme référence?
import numpy as np
from scipy.special import gammainc
from matplotlib import pyplot as plt
def sample(center,radius,n_per_sphere):
r = radius
ndim = center.size
x = np.random.normal(size=(n_per_sphere, ndim))
ssq = np.sum(x**2,axis=1)
fr = r*gammainc(ndim/2,ssq/2)**(1/ndim)/np.sqrt(ssq)
frtiled = np.tile(fr.reshape(n_per_sphere,1),(1,ndim))
p = center + np.multiply(x,frtiled)
return p
fig1 = plt.figure(1)
ax1 = fig1.gca()
center = np.array([0,0])
radius = 1
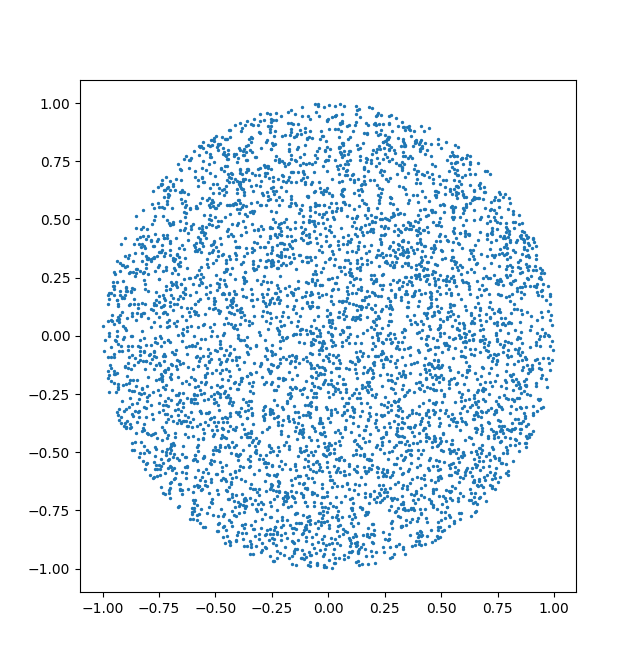
p = sample(center,radius,10000)
ax1.scatter(p[:,0],p[:,1],s=0.5)
ax1.add_artist(plt.Circle(center,radius,fill=False,color='0.5'))
ax1.set_xlim(-1.5,1.5)
ax1.set_ylim(-1.5,1.5)
ax1.set_aspect('equal')
vous pouvez simplement générer des points aléatoires dans coordonnées sphériques (en supposant que vous travaillez en 3D): S(r, θ, φ), où r փ [0, R], θ փ [0, π], φ փ [0, 2π ), où R est le rayon de votre sphère. Cela vous permettrait également de contrôler directement le nombre de points générés (c'est-à-dire que vous n'avez pas besoin de jeter des points).
pour compenser la perte de densité avec le Rayon, vous produisez la coordonnée radiale suivant une puissance distribution du droit (voir réponse de dmckee pour une explication sur la façon de procéder).
si votre code a besoin de coordonnées (x,y,z) (c'est-à-dire cartésiennes), il vous suffit de convertir les points générés au hasard en coordonnées sphériques en coordonnées cartésiennes comme expliqué ici .
import numpy as np
import matplotlib.pyplot as plt
r= 30.*np.sqrt(np.random.rand(1000))
#r= 30.*np.random.rand(1000)
phi = 2. * np.pi * np.random.rand(1000)
x = r * np.cos(phi)
y = r * np.sin(phi)
plt.figure()
plt.plot(x,y,'.')
plt.show()c'est ce que vous voulez