La sélection à la Roulette dans les Algorithmes génétiques
est-ce que quelqu'un peut fournir un pseudo code pour une fonction de sélection de roulette? Comment mettre en œuvre ceci:
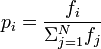
je ne comprends pas vraiment comment lire cette notation mathématique. Je n'ai jamais pris de probabilité ou de statistiques.
12 réponses
Cela fait quelques années que je ne l'ai pas fait moi-même, mais le pseudo-code suivant a été trouvé assez facilement sur google.
for all members of population
sum += fitness of this individual
end for
for all members of population
probability = sum of probabilities + (fitness / sum)
sum of probabilities += probability
end for
loop until new population is full
do this twice
number = Random between 0 and 1
for all members of population
if number > probability but less than next probability
then you have been selected
end for
end
create offspring
end loop
le site d'où cela vient peut être trouvé ici si vous avez besoin de plus de détails.
beaucoup de bonnes solutions déjà, mais je pense que ce code est plus clair.
def select(fs):
p = random.uniform(0, sum(fs))
for i, f in enumerate(fs):
if p <= 0:
break
p -= f
return i
En outre, si vous accumulez les fs, vous pouvez produire une solution plus efficace.
cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]
def select(cfs):
return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))
c'est à la fois plus rapide et c'est un code extrêmement concis. STL en C++ a un algorithme de bisection similaire disponible si c'est le langage que vous utilisez.
le pseudocode affiché contenait certains éléments imprécis, et il ajoute la complexité de générer progéniture au lieu d'effectuer une sélection pure. Voici une implémentation python simple de ce pseudo:
def roulette_select(population, fitnesses, num):
""" Roulette selection, implemented according to:
</q/roulette-selection-in-genetic-algorithms-58498/"""
total_fitness = float(sum(fitnesses))
rel_fitness = [f/total_fitness for f in fitnesses]
# Generate probability intervals for each individual
probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
# Draw new population
new_population = []
for n in xrange(num):
r = rand()
for (i, individual) in enumerate(population):
if r <= probs[i]:
new_population.append(individual)
break
return new_population
c'est ce qu'on appelle la sélection de roue à la roulette par acceptation stochastique:
/// \param[in] f_max maximum fitness of the population
///
/// \return index of the selected individual
///
/// \note Assuming positive fitness. Greater is better.
unsigned rw_selection(double f_max)
{
for (;;)
{
// Select randomly one of the individuals
unsigned i(random_individual());
// The selection is accepted with probability fitness(i) / f_max
if (uniform_random_01() < fitness(i) / f_max)
return i;
}
}
Le nombre moyen de tentatives nécessaires pour une seule sélection est:
τ = f max / avg (f)
- f max est le maximum de fitness de la population
- avg(f) est le taux moyen de remise en forme
τ ne dépendent pas explicitement sur le nombre d'individus dans la population (N), Mais le rapport peut changer avec N.
cependant, dans de nombreuses applications(où le fitness reste limité et le fitness moyen ne diminue pas à 0 pour augmenter N) τ n'augmente pas de façon ininterrompue avec N et donc une complexité typique de cet algorithme est O (1) (la sélection de roue de roulette en utilisant des algorithmes de recherche A O(N) ou o (log N) complexité).
la probabilité la répartition de cette procédure est en effet la même que dans la sélection classique roulette-roue.
pour plus de détails voir:
- Roulette-wheel selection via stochastic acceptance (Adam Liposki, Dorota Lipowska - 2011)
voici un code en C:
// Find the sum of fitnesses. The function fitness(i) should
//return the fitness value for member i**
float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
sumFitness += fitness(i);
// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(rand() % 10000) / 9999.0f) * sumFitness;
// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;
while (randomNumber > partialSum)
{
partialSum += fitness(memberID);
memberID++;
}
**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**
de la réponse ci-dessus, j'ai obtenu ce qui suit, qui était plus clair pour moi que la réponse elle-même.
pour donner un exemple:
Aléatoire(somme) :: Random(12) En itérant à travers la population, nous vérifions ce qui suit: aléatoire < sum
choisissons 7 comme nombre aléatoire.
Index | Fitness | Sum | 7 < Sum
0 | 2 | 2 | false
1 | 3 | 5 | false
2 | 1 | 6 | false
3 | 4 | 10 | true
4 | 2 | 12 | ...
par cet exemple, le plus apte (indice 3) a le pourcentage le plus élevé d'être choisi (33%); Comme le nombre aléatoire il suffit d'atterrir dans les 6 - > 10, et il sera choisi.
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
}
double rand = (((double)rand() / (double)RAND_MAX) * sum);
sum = 0;
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
if (rand < sum) {
//breed i
break;
}
}
Prof. Thrun de Stanford AI lab a également présenté un fast (er? de ré-échantillonnage du code en python au cours de sa CS373 de Udacity. Les résultats de la recherche Google ont conduit au lien suivant:
http://www.udacity-forums.com/cs373/questions/20194/fast-resampling-algorithm
Espérons que cette aide
Voici une implémentation java compacte que j'ai écrite récemment pour la sélection à la roulette, avec un peu de chance d'utilisation.
public static gene rouletteSelection()
{
float totalScore = 0;
float runningScore = 0;
for (gene g : genes)
{
totalScore += g.score;
}
float rnd = (float) (Math.random() * totalScore);
for (gene g : genes)
{
if ( rnd>=runningScore &&
rnd<=runningScore+g.score)
{
return g;
}
runningScore+=g.score;
}
return null;
}
choix de la roue de Roulette dans MatLab:
TotalFitness=sum(Fitness);
ProbSelection=zeros(PopLength,1);
CumProb=zeros(PopLength,1);
for i=1:PopLength
ProbSelection(i)=Fitness(i)/TotalFitness;
if i==1
CumProb(i)=ProbSelection(i);
else
CumProb(i)=CumProb(i-1)+ProbSelection(i);
end
end
SelectInd=rand(PopLength,1);
for i=1:PopLength
flag=0;
for j=1:PopLength
if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
flag=1;
break;
end
end
if(flag==0)
SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
end
end
Based on my research ,Here is another implementation in C# if there is a need for it:
//those with higher fitness get selected wit a large probability
//return-->individuals with highest fitness
private int RouletteSelection()
{
double randomFitness = m_random.NextDouble() * m_totalFitness;
int idx = -1;
int mid;
int first = 0;
int last = m_populationSize -1;
mid = (last - first)/2;
// ArrayList's BinarySearch is for exact values only
// so do this by hand.
while (idx == -1 && first <= last)
{
if (randomFitness < (double)m_fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > (double)m_fitnessTable[mid])
{
first = mid;
}
mid = (first + last)/2;
// lies between i and i+1
if ((last - first) == 1)
idx = last;
}
return idx;
}
Ok, donc il y a 2 méthodes pour sélection de roue de roulette mise en œuvre: habituelle et acceptation Stochastique une.
habituel algorithme:
# there will be some amount of repeating organisms here.
mating_pool = []
all_organisms_in_population.each do |organism|
organism.fitness.times { mating_pool.push(organism) }
end
# [very_fit_organism, very_fit_organism, very_fit_organism, not_so_fit_organism]
return mating_pool.sample #=> random, likely fit, parent!
acceptation Stochastique algorithme:
max_fitness_in_population = all_organisms_in_population.sort_by(:fitness)[0]
loop do
random_parent = all_organisms_in_population.sample
probability = random_parent.fitness/max_fitness_in_population * 100
# if random_parent's fitness is 90%,
# it's very likely that rand(100) is smaller than it.
if rand(100) < probability
return random_parent #=> random, likely fit, parent!
else
next #=> or let's keep on searching for one.
end
end
vous pouvez choisir l'un ou l'autre, ils retourneront des résultats identiques.
ressources Utiles:
http://natureofcode.com/book/chapter-9-the-evolution-of-code -un chapitre clair et convivial sur les algorithmes génétiques. explique choix de roue de roulette comme un seau de lettres en bois (plus que vous mettez dans - le Grand Est la chance de choisir un a, habituel algorithme).
https://en.wikipedia.org/wiki/Fitness_proportionate_selection - décrit acceptation Stochastique algorithme.
j'ai écrit une version en C# et je suis vraiment à la recherche de confirmation qu'elle est en effet correcte:
(roulette_selector est un nombre aléatoire qui sera dans l'intervalle 0,0 à 1,0)
private Individual Select_Roulette(double sum_fitness)
{
Individual ret = new Individual();
bool loop = true;
while (loop)
{
//this will give us a double within the range 0.0 to total fitness
double slice = roulette_selector.NextDouble() * sum_fitness;
double curFitness = 0.0;
foreach (Individual ind in _generation)
{
curFitness += ind.Fitness;
if (curFitness >= slice)
{
loop = false;
ret = ind;
break;
}
}
}
return ret;
}