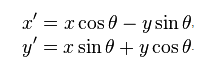Rotation d'un point autour d'un autre point (2D)
J'essaie de faire un jeu de cartes où les cartes se fanent. En ce moment pour l'afficher Im en utilisant L'API Allegro qui a une fonction:
al_draw_rotated_bitmap(OBJECT_TO_ROTATE,CENTER_X,CENTER_Y,X
,Y,DEGREES_TO_ROTATE_IN_RADIANS);
Donc, avec cela, je peux faire mon effet de ventilateur facilement. Le problème est alors de savoir quelle carte est sous la souris. Pour ce faire, j'ai pensé à faire un polygone d'essai de choc. Je ne suis pas sûr de savoir comment faire pivoter les 4 points sur la carte pour constituer le polygone. J'ai essentiellement besoin de faire la même opération que Allegro.
Par exemple, les 4 points de la carte sont:
card.x
card.y
card.x + card.width
card.y + card.height
J'aurais besoin d'une fonction comme:
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
}
Merci
4 réponses
Oh, c'est facile.. soustrayez d'abord le point de pivot (cx,cy), puis faites-le pivoter, puis ajoutez à nouveau le point.
Non testé:
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
float s = sin(angle);
float c = cos(angle);
// translate point back to origin:
p.x -= cx;
p.y -= cy;
// rotate point
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;
// translate point back:
p.x = xnew + cx;
p.y = ynew + cy;
return p;
}
Si vous tournez point (px, py) autour du point (ox, oy) par l'angle thêta vous obtiendrez:
p'x = cos(theta) * (px-ox) - sin(theta) * (py-oy) + ox
p'y = sin(theta) * (px-ox) + cos(theta) * (py-oy) + oy
C'est un moyen facile de faire pivoter un point en 2D.
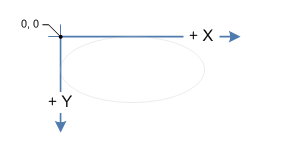
Le système de coordonnées à l'écran est gaucher, c'est-à-dire que la coordonnée x augmente de gauche à droite et la coordonnée y augmente de haut en bas. L'origine O(0, 0) est dans le coin supérieur gauche de l'écran.
Un dans le sens des aiguilles rotation autour de l'origine d'un point de coordonnées (x, y) est donnée par les équations suivantes:
Où (x', y') sont les coordonnées de le point après rotation et l'angle thêta, l'angle de rotation (doit être en radians, c'est-à-dire multiplié par: PI / 180).
Pour effectuer une rotation autour d'un point différent de L'origine O (0,0), disons point A(A, B) (point de pivot). Tout d'abord, nous traduisons le point à faire pivoter, c'est - à - dire (x, y) à l'origine, en soustrayant les coordonnées du point de pivot, (x-a, Y-b). Ensuite, nous effectuons la rotation et obtenons les nouvelles coordonnées (x', y') et finalement nous traduisons le point en arrière, par ajout des coordonnées du point pivot aux nouvelles coordonnées (x '+ a, y ' + b).
Suivant la description ci-dessus:
Un 2D dans le sens des aiguilles d'une montre degrés thêta rotation du point (x, Y) autour du point (a, B) est:
En utilisant votre prototype de fonction: (x, y) -> (p. x, P. y); (a, b) -> (cx, cy); THETA -> angle:
POINT rotate_point(float cx, float cy, float angle, POINT p){
return POINT(cos(angle) * (p.x - cx) - sin(angle) * (p.y - cy) + cx,
sin(angle) * (p.x - cx) + cos(angle) * (p.y - cy) + cy);
}
float s = sin(angle); // angle is in radians
float c = cos(angle); // angle is in radians
Pour rotation dans le sens horaire:
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;
Pour une rotation dans le sens antihoraire:
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;