Représentant les anneaux d'entiers algébriques
je suis en train de représenter l'anneau;
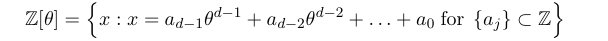
Cette bague est un sous-anneau des entiers algébriques, qui lui-même est un sous-anneau du champ;
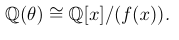
je peux représenter ce champ avec sympy AlgebraicField classe
Q_theta = sympy.polys.domains.AlgebraicField(QQ,theta)
y a-t-il un moyen de représenter le sous-ensemble entier ci-dessus dans un de façon similaire?
2 réponses
je soupçonne peut-être pas une fonctionnalité sympy pour ces raisons:
Premier, si theta est algébrique sur les entiers, alors attenante thêta à un polynôme anneau sur les entiers, est isomorphe.
par exemple, pi n'est pas algébrique sur les entiers, car il n'y a pas de coefficients entiers qui, combinés avec pi et les pouvoirs de pi, seront égaux à zéro.
Pour prouver que ces, sont en fait, isomorphe, il suffit de prendre l'homomorphisme de l'anneau d'évaluation qui évalue chaque polynôme à pi.
ceci peut ne pas être une fonctionnalité prête, parce que calculer si un nombre n'est pas algébrique sur un anneau est non-trivial. Par exemple, déterminer si oui ou non e + pi l'algébrique reste une question ouverte.
ceci peut être réalisé en sympy par
from sympy.polys.domains import ZZ, QQ, RR, FF, EX
x, y, z, t = symbols('x y z t')
ZZ['theta']
ou
ZZ[t]
on peut facilement tester que cela, en fait, de vous donner les anneau de polynômes sur les entiers.
Deuxième, nombres qui sont algébrique, (nombres comme le nombre imaginaire i, qui sont les racines des polynômes à valeur entière) peut être obtenue en prenant le modulo de l'anneau polynomial et l'idée générée par son polynôme Monique unique.
donc si theta est le nombre imaginaire i, qui a le polynôme unique Monique x^2+1
>>> QQ.old_poly_ring(x).ideal(x**2+1)
<x**2 + 1>
>>> ZZ.old_poly_ring(x).ideal(x**2+1)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/domains/ring.py", line 91, in ideal
return ModuleImplementedIdeal(self, self.free_module(1).submodule(
File "/usr/local/lib/python2.7/dist- packages/sympy/polys/domains/old_polynomialring.py", line 192, in free_module
return FreeModulePolyRing(self, rank)
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/agca/modules.py", line 455, in __init__
+ 'got %s' % ring.dom)
NotImplementedError: Ground domain must be a field, got ZZ
de plus, en essayant ceci:
>>> QQ.old_poly_ring(x).quotient_ring([x**2])
QQ[x]/<x**2>
>>> ZZ.old_poly_ring(x).quotient_ring([x**2])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/domains/ring.py", line 115, in quotient_ring
e = self.ideal(*e)
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/domains/ring.py", line 91, in ideal
return ModuleImplementedIdeal(self, self.free_module(1).submodule(
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/domains/old_polynomialring.py", line 192, in free_module
return FreeModulePolyRing(self, rank)
File "/usr/local/lib/python2.7/dist-packages/sympy/polys/agca/modules.py", line 455, in __init__
+ 'got %s' % ring.dom)
NotImplementedError: Ground domain must be a field, got ZZ
cependant, la fonctionnalité utile n'est implémentée que pour les anneaux polynomiaux au-dessus des champs, et pour diverses localisations et quotients de celles-ci.
en bref, à moins que theta ne soit pas algébrique sur les entiers, cela pourrait être impossible dans le cadre de sympy.
cependant, représentant des anneaux de cette manière peut être réalisé en faisant des classes et utiliser les méthodes magiques de Python pour outrepasser le comportement normal de + et *, qui est essentiellement ce dont nous avons besoin pour étudier les anneaux.
Voici un exemple de l' Nombres Entiers Gaussiens mentionné ci-dessus. Ce code pourrait facilement être réutilisées à vous donner, par exemple, la racine carrée de 2, ou tout autre nombre algébrique sur les entiers.
Physicien ici: j'ai compris certains de ces mots, mais peut-être que je peux vous aider quand même: - D
Avez-vous essayé SymPyIntegerRing