Supprimer les doublons d'une liste dans Haskell

votre code et nubO(N^2) complexité.

Vous pouvez améliorer la complexité de O(N log N) et évitez d'utiliser elem par tri, de regroupement, et en ne prenant que le premier élément de chaque groupe.

sur le plan Conceptuel,

rmdups :: (Ord a) => [a] -> [a]
rmdups = map head . group . sort

supposons que vous commenciez par la liste [1, 2, 1, 3, 2, 4]. En triant, vous obtenez, [1, 1, 2, 2, 3, 4]; par le groupement que, vous obtenez, [[1, 1], [2, 2], [3], [4]]; enfin, en prenant la tête de chaque liste, vous obtenez [1, 2, 3, 4].

Le plein la mise en oeuvre de ce qui précède implique simplement l'élargissement de chaque fonction.

Notez que cela nécessite le plus fort Ord contrainte sur les éléments de la liste, et modifie également leur ordre dans la liste retournée.

Encore plus facile.

import Data.Set 
mkUniq :: Ord a => [a] -> [a]
mkUniq = toList . fromList

Convertir l'ensemble d'une liste d'éléments O (n) heure:

toList :: Set a -> [a]

Créer un jeu à partir d'une liste d'éléments O (N log n) heure:

fromList :: Ord a => [a] -> Set a

en python ce ne serait pas différent.

def mkUniq(x): 
   return list(set(x)))

comme la solution de @scvalex, la suivante a un O(n * log n) complexité et un Ord la dépendance. A la différence de, il conserve l'ordre, en gardant la première fois des éléments.

import qualified Data.Set as Set

rmdups :: Ord a => [a] -> [a]
rmdups = rmdups' Set.empty where
  rmdups' _ [] = []
  rmdups' a (b : c) = if Set.member b a
    then rmdups' a c
    else b : rmdups' (Set.insert b a) c

résultats des analyses comparatives

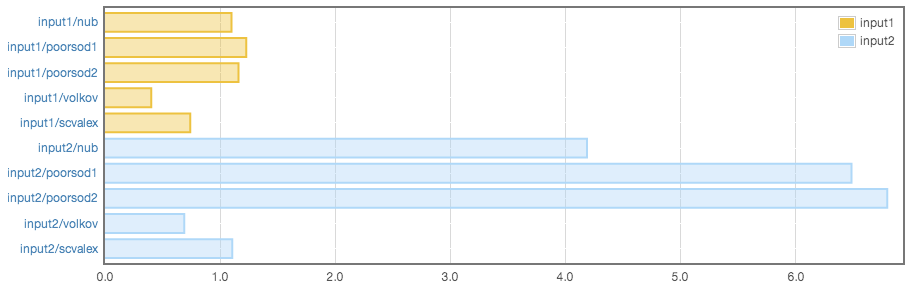
comme vous pouvez le voir, les résultats du benchmark prouvent que cette solution est la plus efficace. Vous pouvez trouver la source de ce benchmark ici.

en utilisant la récursivité-régimes d':

import Data.Functor.Foldable

dedup :: (Eq a) => [a] -> [a]
dedup = para pseudoalgebra
    where pseudoalgebra Nil                 = []
          pseudoalgebra (Cons x (past, xs)) = if x `elem` past then xs else x:xs

bien que ce soit certainement plus avancé, je pense qu'il est assez élégant et montre certains paradigmes de programmation fonctionnelle valables.

...ou en utilisant la fonction union à partir de données.Liste applique à soi-même:

import Data.List

unique x = union x x

il est trop tard pour répondre à cette question mais je veux partager ma solution qui est originale sans utiliser elem et ne supposez pas Ord.

rmdups' :: (Eq a) => [a] -> [a]
rmdups' [] = []
rmdups' [x] = [x]
rmdups' (x:xs) = x : [ k  | k <- rmdups'(xs), k /=x ]

cette solution supprime les doublons à la fin de la saisie, tandis que la mise en œuvre des questions supprime au début. Par exemple,

rmdups "maximum-minimum"
-- "ax-nium"

rmdups' "maximum-minimum"
-- ""maxiu-n"

en outre, cette complexité de code est O(N*K) où N est la longueur de la chaîne et K est le nombre de caractères uniques dans la chaîne. N > = K ainsi, il sera O (N^2) dans le pire des cas mais cela signifie qu'il n'y a pas de répétition dans la chaîne et c'est différent puisque vous essayez de supprimer les doublons dans la chaîne.

Graham Hutton a un programmation À Haskell. Il conserve l'ordre. Elle est comme suit.

rmdups :: Eq a => [a] -> [a]
rmdups [] = []
rmdups (x:xs) = x : filter (/= x) (rmdups xs)
rmdups "maximum-minimum"

"maxiu-n"

cela me dérangeait jusqu'à ce que je voie la fonction de Hutton. Puis, j'ai essayé, encore. Il y a deux versions, la première conserve le dernier duplicata, la seconde conserve le premier.

rmdups ls = [d|(z,d)<- zip [0..] ls, notElem d $ take z ls]
rmdups "maximum-minimum"

"maxiu-n"

Si vous voulez prendre le tout d'abord, et non pas les derniers éléments dupliqués de la liste, comme vous essayez de le faire, il suffit de changer takedrop dans la fonction et de modifier l'énumération zip [0..]zip [1..].