Supprimer le fond blanc d'une image et le rendre transparent
nous essayons de faire ce qui suit dans Mathematica:
RMagick supprimer le fond blanc de l'image et le rendre transparent
mais avec des photos réelles il finit par sembler moche (comme avoir un halo autour de l'image).
voici ce que nous avons essayé jusqu'à présent:
unground0[img_] := With[{mask = ChanVeseBinarize[img, TargetColor->{1.,1.,1.}]},
Rasterize[SetAlphaChannel[img, ImageApply[1-#&, mask]], Background->None]]]
Voici un exemple de ce que cela fait.
image originale:

Image avec le fond blanc remplacé par aucun fond (ou, pour les fins de démonstration ici, un fond rose):

des idées pour se débarrasser de ce halo? En modifiant des choses comme LevelPenalty, Je ne peux faire disparaître le halo qu'au prix de perdre une partie de l'image.
Modifier: pour que je puisse comparer des solutions pour le bounty, s'il vous plaît structurer votre solution comme ci-dessus, à savoir une fonction autonome appelée unground-quelque chose qui prend une image et renvoie une image avec fond transparent. Merci beaucoup, tout le monde!
9 réponses
peut-être, selon la qualité de bord dont vous avez besoin:
img = Import@"http://i.stack.imgur.com/k7E1F.png";
mask = ChanVeseBinarize[img, TargetColor -> {1., 1., 1.}, "LengthPenalty" -> 10]
mask1 = Blur[Erosion[ColorNegate[mask], 2], 5]
Rasterize[SetAlphaChannel[img, mask1], Background -> None]

Modifier
img2 = Import@"http://i.stack.imgur.com/k7E1F.png";
(*key point:scale up image to smooth the edges*)
img = ImageResize[img2, 4 ImageDimensions[img2]];
mask = ChanVeseBinarize[img, TargetColor -> {1., 1., 1.}, "LengthPenalty" -> 10];
mask1 = Blur[Erosion[ColorNegate[mask], 8], 10];
f[col_] := Rasterize[SetAlphaChannel[img, mask1], Background -> col,
ImageSize -> ImageDimensions@img2]
GraphicsGrid[{{f@Red, f@Blue, f@Green}}]
Edit 2
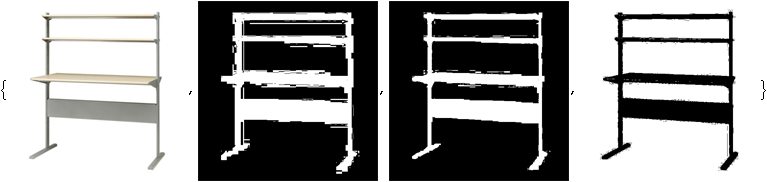
juste pour avoir une idée de l'étendue du halo et des imperfections de fond dans l'image:
img = Import@"http://i.stack.imgur.com/k7E1F.png";
Join[{img}, MapThread[Binarize, {ColorSeparate[img, "HSB"], {.01, .01, .99}}]]
ColorNegate@ImageAdd[EntropyFilter[img, 1] // ImageAdjust, ColorNegate@img]

cette fonction implémente le mélange inversé décrit par Mark Ransom, pour une amélioration supplémentaire petite mais visible:
reverseBlend[img_Image, alpha_Image, bgcolor_] :=
With[
{c = ImageData[img],
a = ImageData[alpha] + 0.0001, (* this is to minimize ComplexInfinitys and considerably improve performance *)
bc = bgcolor},
ImageClip@
Image[Quiet[(c - bc (1 - a))/a, {Power::infy,
Infinity::indet}] /. {ComplexInfinity -> 0, Indeterminate -> 0}]
]
c'est la fonction de suppression de l'arrière-plan. Le paramètre threshold est utilisé pour la binarisation initiale de l'image, le minSizeCorrection est pour ajuster la limite de taille des petites composantes de camelote à enlever après la binarisation.
removeWhiteBackground[img_, threshold_: 0.05, minSizeCorrection_: 1] :=
Module[
{dim, bigmask, mask, edgemask, alpha},
dim = ImageDimensions[img];
bigmask =
DeleteSmallComponents[
ColorNegate@
MorphologicalBinarize[ColorNegate@ImageResize[img, 4 dim], threshold],
Round[minSizeCorrection Times @@ dim/5]];
mask = ColorNegate@
ImageResize[ColorConvert[bigmask, "GrayScale"], dim];
edgemask =
ImageResize[
ImageAdjust@DistanceTransform@Dilation[EdgeDetect[bigmask, 2], 6],
dim];
alpha =
ImageAdd[
ImageSubtract[
ImageMultiply[ColorNegate@ColorConvert[img, "GrayScale"],
edgemask], ImageMultiply[mask, edgemask]], mask];
SetAlphaChannel[reverseBlend[img, alpha, 1], alpha]
]
tester la fonction:
img = Import["http://i.stack.imgur.com/k7E1F.png"];
background =
ImageCrop[
Import["http://cdn.zmescience.com/wp-content/uploads/2011/06/\
forest2.jpg"], ImageDimensions[img]];
result = removeWhiteBackground[img]
ImageCompose[background, result]
Rasterize[result, Background -> Red]
Rasterize[result, Background -> Black]
Brève Explication de son fonctionnement:
-
choisissez votre méthode préférée de binariaztion qui produit des arêtes vives relativement précises "15199090920"
-
appliquez-le à une image agrandie, puis réduisez le
maskobtenu à la taille originale. Cela nous donne l'anticrénelage. La plupart du travail est fait. -
pour une petite amélioration, mélanger l'image sur le fond en utilisant la luminosité de son négatif comme alpha, puis mélanger l'image obtenue au-dessus de l'original dans une région mince autour des bords (
edgemask) pour réduire la visibilité des pixels blancs sur les bords. Le canal alpha correspondant à ces opérations est calculé (expression quelque peu cryptiqueImageMultiply/Add). -
nous avons maintenant une estimation de le canal alpha pour faire un mélange inversé.
les étapes 3 et 4 ne s'améliorent pas beaucoup, mais la différence est visible.
je vais parler de façon générique, pas spécifiquement en référence à Mathematica. Je n'ai aucune idée si ces opérations sont difficiles ou triviales.
La première étape consiste à estimer l'alpha (transparence) pour les pixels sur le bord de l'image. En ce moment vous utilisez un seuil strict, Donc l'alpha est soit 0% totalement transparent ou 100% totalement opaque. Vous devez définir une gamme entre le blanc total de l'arrière-plan et les couleurs qui sont indiscutablement une partie de l'image, et de définir une proportion appropriée - si elle est plus proche en couleur à l'arrière-plan, il est faible alpha, et si elle est plus proche de la coupure plus sombre alors il est un alpha élevé. Après cela, vous pouvez faire des ajustements basés sur les valeurs alpha environnantes - plus un pixel est entouré de transparence, plus il est susceptible d'être transparent lui-même.
une fois que vous avez des valeurs alpha, vous devez faire un mélange inverse pour obtenir la bonne couleur. Lorsqu'une image est affichée sur un fond il est mélangé selon la valeur alpha en utilisant la formule c = bc*(1-a)+fc*a où bc est la couleur de fond et fc est la couleur de premier plan. Dans votre cas, le fond est blanc (255,255,255) et la couleur du premier plan est l'inconnu, donc nous inversons la formule: fc = (c - bc*(1-a))/a . Quand a=0 la formule appelle à une division par zéro, mais la couleur n'a pas d'importance de toute façon donc utilisez juste le noir ou le blanc.
Voici un essai à la mise en œuvre de Marque Rançon de l'approche, avec l'aide de bélisaire masque de la génération:
localise la limite de l'objet:
img1 = SetAlphaChannel[img, 1];
erosionamount=2;
mb = ColorNegate@ChanVeseBinarize[img, TargetColor -> {1., 1., 1},
"LengthPenalty" -> 10];
edge = ImageSubtract[Dilation[mb, 2], Erosion[mb, erosionamount]];
ImageApply[{1, 0, 0} &, img, Masking ->edge]

définit les valeurs alpha:
edgealpha = ImageMultiply[ImageFilter[(1 - Mean[Flatten[#]]^5) &,
ColorConvert[img, "GrayScale"], 2, Masking -> edge], edge];
imagealpha = ImageAdd[edgealpha, Erosion[mb, erosionamount]];
img2 = SetAlphaChannel[img, imagealpha];
img3 = ImageApply[Module[{c, \[Alpha], bc, fc},
bc = {1, 1, 1};
c = {#[[1]], #[[2]], #[[3]]};
\[Alpha] = #[[4]];
If[\[Alpha] > 0, Flatten[{(c - bc (1 - \[Alpha]))/\[Alpha], \[Alpha]}], {0., 0.,
0., 0}]] &, img2];
Show[img3, Background -> Pink]

remarquez que certains bords sont blancs fuzz? Comparez cela avec le contour rouge de la première image. Il nous faut un meilleur détecteur de bord. Augmenter la quantité d'érosion aide avec le fuzz, mais alors les autres côtés deviennent trop transparents, il y a donc un compromis sur la largeur du masque de bord. C'est assez bon, cependant, considérant qu'il n'y a pas d'opération flou, en soi.
Il serait instructif d'exécuter l'algorithme sur une variété d'images pour tester sa robustesse, pour voir comment automatique, il est.
juste jouer comme un débutant - il est étonnant de voir combien d'outils sont disponibles.
b = ColorNegate[
GaussianFilter[MorphologicalBinarize[i, {0.96, 0.999}], 6]];
c = SetAlphaChannel[i, b];
Show[Graphics[Rectangle[], Background -> Orange,
PlotRangePadding -> None], c]

je suis complètement nouveau dans le traitement d'image mais voici ce que j'obtiens après avoir joué avec de nouvelles fonctions de traitement d'image morphologique de la version 8:
mask = DeleteSmallComponents[
ColorNegate@
Image[MorphologicalComponents[ColorNegate@img, .062,
Method -> "Convex"], "Bit"], 10000];
Show[Graphics[Rectangle[], Background -> Red,
PlotRangePadding -> None], SetAlphaChannel[img, ColorNegate@mask]]

je recommande D'utiliser Photoshop pour cela et de sauvegarder en PNG.
mesures possibles à prendre:
- dilater le masque
- flou
- utiliser le masque, régler la transparence par la distance du blanc
- à l'aide du masque, ajuster la saturation de telle sorte que les couleurs auparavant plus blanches sont plus saturées.
il suffit de remplacer n'importe quel pixel qui est" presque proche du blanc " par un pixel de la même couleur RGB et un gradient sigmoïde sur le canal de transparence. Vous pouvez appliquer la transition linéaire du solide au transparent, mais sinusoïde ou Sigmoid ou Tanh semblent plus naturel, en fonction de la netteté du bord que vous recherchez, ils se déplacent rapidement loin du milieu à soit solide ou transparent, mais pas de manière progressive/binaire, ce qui est ce que vous avez maintenant.
pensez-y de cette façon:
disons R, G, B sont chacun 0.0-1.0, alors représentons blanc comme un nombre simple comme R+G+B=1.0*3=3.0.
en Prenant un peu de chaque couleur fait un peu "off-white", mais en prenant un peu de tous les 3 est beaucoup plus qu'un peu à l'écart de tout. Disons que vous autorisez une réduction de 10% sur n'importe quel canal: 1.0*.10 = .1, répartissez cette perte sur les trois et liez-la entre 0 et 1 pour le canal alpha, si elle est inférieure à .Un, tel que (perte = 0,9) = >0 et (perte = 1,0)=>1:
threshold=.10;
maxLoss=1.0*threshold;
loss=3.0-(R+G+B);
alpha=If[loss>maxLoss,0,loss/maxLoss];
(* linear scaling is used above *)
(* or use 1/(1 + Exp[-10(loss - 0.5maxLoss)/maxLoss]) to set sigmoid alpha *)
(* Log decay: Log[maxLoss]/Log[loss]
(for loss and maxLoss <1, when using RGB 0-255, divide by 255 to use this one *)
setNewPixel[R,G,B,alpha];
pour référence:
maxLoss = .1;
Plot[{ 1/(1 + Exp[-10(loss - 0.5maxLoss)/maxLoss]),
Log[maxLoss]/Log[loss],
loss/maxLoss
}, {loss, 0, maxLoss}]
Le seul danger (ou de profit?) vous avez dans cela, est que cela ne se soucie pas des blancs qui font réellement partie de la photo. Il élimine tous les blancs. Donc, si vous avez une photo de voiture blanche, il finira par avoir des taches transparentes dans elle. Mais de votre exemple, cela semble être un effet désiré.

