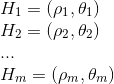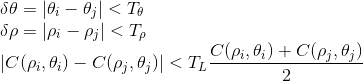Détection de Rectangle avec transformation de Hough

Pour ceux d'entre vous interrogez sur le papier, c'est:

détection de Rectangle basée sur une transformation de Hough fendue par Cláudio Rosito Jung et Rodrigo Schramm.

maintenant, selon le document, les points d'intersection sont exprimés en coordonnées polaires, évidemment votre mise en œuvre peut être différente (la seule façon de dire est de nous montrer votre code).

en supposant que vous êtes cohérent avec sa notation, vos pics doivent être exprimés comme:

vous devez alors effectuer l'analyse de crête donnée par l'équation (3) dans la section 4.3 ou

où 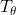représente le seuil angulaire correspondant aux lignes parallèles et 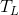est le seuil normalisé correspondant à des lignes de longueur similaire.

la précision de L'Espace Hough devrait dépendre de deux facteurs principaux.

l'accumulateur est relié à L'Espace. Pour passer en boucle à travers le réseau d'accumulateurs, l'accumulateur doit diviser l'Espace Hough en une grille discrète.

Quelques idées pour vous y aider.

1. placer l'origine directement à la centre de l'image. par opposition à en utilisant le bas à gauche ou le haut à gauche d'une image en code.
2. essayez d'utiliser l'image la plus proche possible obtenir un carré. le plus allongé un l'image est pour une zone donnée la plus prononcé l' piège de résolution devient sur les bords
3. essayez de diviser votre image en 28/08/16 etc accumulateurs différents avec une origine au centre de cette sous-image. Il faudra un peu de sur-place pour relier les résultats de chaque accumulateur ensemble pour la détection de rectangle, mais il devrait aider répartissez la résolution de façon plus égale.
4. la solution ultime serait d'augmenter la résolution dépend de façon linéaire de la la distance de l'origine. ceci peut être réalisé en utilisant le

    (x-a)^2 + (y-b)^2 = \rho^2

circle equation where
    - x,y are the current pixel
    - a,b are your chosen origin
    - \rho is the radius
once the radius is known adjust your accumulator
resolution accordingly. You will have to keep
track of the center of each \rho \theta bin.
for transforming back to Cartesian

le lien vers le document référencé ne fonctionne pas, mais si vous avez utilisé la transformation de hough standard, les quatre points d'intersection seront exprimés en coordonnées cartésiennes. En fait, les quatre lignes détectées avec la transformation de hough seront exprimées en utilisant la "paramétrisation normale":

rho = x cos(theta) + y sin(theta)

vous aurez donc quatre paires (rho_i, theta_i) qui identifient vos quatre lignes. Après avoir vérifié l'orthogonalité (par exemple juste en comparant les angles theta_i) vous résolvez quatre equation system chacune des formes:

rho_j = x cos(theta_j) + y sin(theta_j)
rho_k = x cos(theta_k) + y sin(theta_k)

où x et y sont les inconnues qui représente les coordonnées cartésiennes du point d'intersection.

je ne suis pas un mathématicien. Je suis disposé à être corrigé...

De Hough 2)... toute ligne sur le plan xy peut être décrite comme p = x cos theta + y sin theta. Dans cette représentation, p est la distance normale et thêta est l'angle normal d'une ligne droite ... Dans les applications pratiques, les angles thêta et les distances p sont quantifiés, et nous obtenons un tableau C (P, theta).

de la géométrie analytique des tables de maths standard du CRC, Polar Coordonnées dans une section Plane ... Une telle paire ordonnée de nombres (R, thêta) sont appelées coordonnées polaires du point P. Lignes droites: let p = distance de la ligne par rapport à O, w = angle dans le sens antihoraire de OX à la perpendiculaire passant par O à la ligne. Forme normale: r cos (theta-w) = p. D'où je conclus que les points se trouvent dans l'espace de coordonnées polaires.