Structure de données de file d'attente prenant en charge la recherche rapide de k-ème élément le plus grand
Je suis confronté à un problème qui nécessite une structure de données de file d'attente prenant en charge la recherche rapide de k-ème élément le plus grand.
Les exigences de cette structure de données sont les suivantes:
Les éléments de la file d'attente ne sont pas nécessairement des entiers, mais ils doivent être comparables les uns aux autres, c'est-à-dire que nous pouvons dire lequel est le plus grand lorsque nous comparons deux éléments(ils peuvent également être égaux).
La structure de données doit prendre en charge la file d'attente (ajoute l'élément à la queue) et dequeue (supprime l'élément en tête).
Il peut rapidement trouver le K-ème plus grand élément dans la file d'attente, pls note k est pas une constante.
Vous pouvez supposer que les opérations mise en file d'attente , dequeue et K-ème plus grand élément de recherche se produisent tous avec la même fréquence.
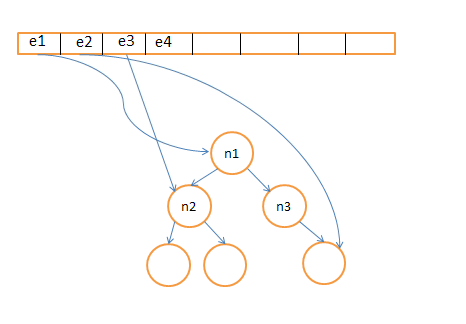
Mon idée est d'utiliser un arbre de recherche binaire équilibré modifié. L'arbre est le même que l'arbre de recherche binaire équilibré ordinaire sauf que chaque nœud i est augmenté avec un autre champ n, je, n, je indique le nombre de nœuds contenus dans le sous-arbre avec nœud racine, je. Les opérations susmentionnées sont prises en charge comme suit:
Pour simplifier, supposons que tous les éléments sont distincts.
Enqueue (x) : x est d'abord inséré dans l'arborescence, supposons que le nœud correspondant soit node t , nous ajoutons pair (X, pointeur vers node t ) à la file d'attente.
Dequeue: supposons que (e1, nœud1) est l'élément à la tête de nœud1 est le pointeur dans l'arbre correspondant à e1. Nous supprimons le nœud1 de l'arborescence et supprimer (E1, noeud1) de la file d'attente.
K-ième plus grand élément de trouver: supposons que le nœud racine est le nœudracine, ses deux enfants sont nodegauche et noeuddroit(supposons qu'elles existent), nous comparons K avec nracine , trois cas peuvent se produire:
Si Kgauche, nous trouvons la K-ième plus grand élément dans le sous-arbre gauche de nracine;
Si K>nracine ndroit, nous trouvons la (K-nracine+ndroit)-e plus grand élément dans le sous-arbre droit de nracine;
Autrement nracine, qui est le nœud que nous voulons.
La complexité temporelle des trois opérations est O (log N ), où N est le nombre d'éléments actuellement dans le file.
Comment puis-je accélérer les opérations mentionnées ci-dessus? Avec quelles structures de données et comment?
3 réponses
Note - vous ne pouvez pas obtenir mieux que O(logn) pour tous, au mieux, vous devez "choisir" quel op vous aimez le plus. (Sinon, vous pouvez trier O(n) en alimentant le tableau à la DS, et en interrogeant 1st, 2nd, 3rd,... nième élément)
- en utilisant une liste de saut au lieu d'une BST équilibrée comme structure triée
peut réduire dequeue complexité à
O(1)cas Moyen . Il n' n'affecte pas la complexité de tout autre op.
pour supprimer d'une liste de saut-tout ce que vous besoin de faire est d'arriver à l'élément en utilisant le pointeur de la tête de la file d'attente, et suivez les liens et supprimer chacun. Le nombre attendu de nœuds à supprimer est 1 + 1/2 + 1/4 + ... = 2. -
trouver Kth peut être atteint dans
O(logK)en commençant par le nœud le plus à gauche (et non la racine) et en vous frayant un chemin jusqu'à ce que vous trouviez que vous avez "plus de fils alors nécessaires", puis traitez le nœud juste trouvé comme la racine tout comme l'algorithme dans la question. Bien qu'il soit meilleur dans complexité asymptotique - le facteur constant est double.
J'ai trouvé un article intéressant:
Requêtes Top-K à Fenêtre coulissante sur les flux incertains publiées dans VLDB 2008 et citées par 71.
Https://www.cse.ust.hk/ ~ yike / wtopk. pdf
VLDB est la meilleure conférence dans le domaine de la recherche de base de données, et le nombre de citations prouve que la structure de données fonctionne réellement.
Le papier semble assez difficile, mais si vous avez vraiment besoin d'améliorer votre structure de données, je vous suggère de lire cet article ou ces articles dans la page de référence de ce papier.
Vous pouvez également utiliser un arbre de doigt .
Par exemple, une file d'attente prioritaire peut être implémentée en étiquetant les nœuds internes par la priorité minimale de ses enfants dans l'arbre, ou une liste/tableau indexé peut être implémentée avec un étiquetage des nœuds par le nombre de feuilles dans leurs enfants. Les arbres de doigt peuvent fournir amorti O(1) contre, Inverser, cdr, o(log n) ajouter et diviser; et peuvent être adaptés pour être indexés ou ordonnés séquences.
Notez également que une structure purement fonctionnelle en fait un bon choix pour une utilisation simultanée.