Courbe De Bézier Quadratique: Calculer Les Points
j'aimerais calculer un point sur une courbe quadratique. Pour l'utiliser avec l'élément canvas de HTML5.
quand j'utilise le quadraticCurveTo() fonction en JavaScript, j'ai un point source, un point cible et un point de contrôle.
Comment puis-je calculer un point sur la courbe quadratique créée à disons t=0.5 avec "seulement" sachant ces trois points?
4 réponses
utilisez la formule de Bézier quadratique, trouvée, par exemple, sur la page Wikipedia pour courbes de Bézier :
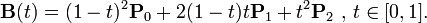
en pseudo-code, c'est
t = 0.5; // given example value
x = (1 - t) * (1 - t) * p[0].x + 2 * (1 - t) * t * p[1].x + t * t * p[2].x;
y = (1 - t) * (1 - t) * p[0].y + 2 * (1 - t) * t * p[1].y + t * t * p[2].y;
p[0] est le point de départ, p[1] est le point de contrôle, et p[2] est le point final. t est le paramètre qui va de 0 à 1.
dans le cas où quelqu'un a besoin de la forme cubique:
//B(t) = (1-t)**3 p0 + 3(1 - t)**2 t P1 + 3(1-t)t**2 P2 + t**3 P3
x = (1-t)*(1-t)*(1-t)*p0x + 3*(1-t)*(1-t)*t*p1x + 3*(1-t)*t*t*p2x + t*t*t*p3x;
y = (1-t)*(1-t)*(1-t)*p0y + 3*(1-t)*(1-t)*t*p1y + 3*(1-t)*t*t*p2y + t*t*t*p3y;
si quelqu'un a besoin de la nième forme, voici l'algorithme. Vous lui donnez N points et il retournera un tableau de N + (N-1) + (N-2) ... points, ce qui résout à (N * (N*1)) / 2 . Le dernier point est la position sur la courbe pour la valeur donnée de T.
9
7 8
4 5 6
0 1 2 3
vous alimentez l'algorithme 0 1 2 3 comme points de contrôle, et ceux les positions seraient le reste du tableau. Le dernier point (9) est la valeur que vous souhaitez.
c'est aussi la façon dont vous subdivisez une courbe bezier, vous lui donnez la valeur de t vous voulez puis vous déclarez la courbe subdivisée comme les côtés de la pyramide. Ensuite, vous indexer les différents points sur le côté de la pyramide et de l'autre côté de la pyramide construite à partir de la base. Ainsi par exemple dans quintic:
E
C D
9 A B
5 6 7 8
0 1 2 3 4
(Pardon l'hexagone, je le voulais joli)
vous indexez les deux courbes parfaitement subdivisées à 0, 5, 9, C, E et E, D, B, 8, 4. Remarquez que la première courbe commence avec un point de contrôle (0) et se termine sur un point de la courbe (E) et que la deuxième courbe Commence sur la courbe (E) et se termine sur le point de contrôle (4). Le nouveau point de contrôle reliant les deux courbes se trouve sur la courbe.
/**
* Performs deCasteljau's algorithm for a bezier curve defined by the given control points.
*
* A cubic for example requires four points. So it should get at least an array of 8 values
*
* @param controlpoints (x,y) coord list of the Bezier curve.
* @param returnArray Array to store the solved points. (can be null)
* @param t Amount through the curve we are looking at.
* @return returnArray
*/
public static float[] deCasteljau(float[] controlpoints, float[] returnArray, float t) {
int m = controlpoints.length;
int sizeRequired = (m/2) * ((m/2) + 1);
if (returnArray == null) returnArray = new float[sizeRequired];
if (sizeRequired > returnArray.length) returnArray = Arrays.copyOf(controlpoints, sizeRequired); //insure capacity
else System.arraycopy(controlpoints,0,returnArray,0,controlpoints.length);
int index = m; //start after the control points.
int skip = m-2; //skip if first compare is the last control point.
for (int i = 0, s = returnArray.length - 2; i < s; i+=2) {
if (i == skip) {
m = m - 2;
skip += m;
continue;
}
returnArray[index++] = (t * (returnArray[i + 2] - returnArray[i])) + returnArray[i];
returnArray[index++] = (t * (returnArray[i + 3] - returnArray[i + 1])) + returnArray[i + 1];
}
return returnArray;
}
(dans le cas où vous êtes étonnant, non, c'est pas vraiment la peine. SVG a raison de s'arrêter à cubic).
j'ai créé cette démo:
// x = a * (1-t)³ + b * 3 * (1-t)²t + c * 3 * (1-t)t² + d * t³
//------------------------------------------------------------
// x = a - 3at + 3at² - at³
// + 3bt - 6bt² + 3bt³
// + 3ct² - 3ct³
// + dt³
//--------------------------------
// x = - at³ + 3bt³ - 3ct³ + dt³
// + 3at² - 6bt² + 3ct²
// - 3at + 3bt
// + a
//--------------------------------
// 0 = t³ (-a+3b-3c+d) + => A
// t² (3a-6b+3c) + => B
// t (-3a+3b) + => c
// a - x => D
//--------------------------------
var A = d - 3*c + 3*b - a,
B = 3*c - 6*b + 3*a,
C = 3*b - 3*a,
D = a-x;
// So we need to solve At³ + Bt² + Ct + D = 0
peut aider quelqu'un.
juste une note: si vous utilisez les formules habituelles présentées ici, alors ne vous attendez pas à ce que t = 0.5 renvoie le point à la moitié de la longueur de la courbe.. Dans la plupart des cas, non.
Plus sur cette ici sous "§23 de Traçage d'une courbe à des intervalles de distance" et ici .