Python: ajustement gaussien à deux courbes avec les moindres carrés non linéaires
ma connaissance des mathématiques est limitée, c'est pourquoi je suis probablement coincé. J'ai un spectre auquel j'essaie de coller deux pics gaussiens. Je peux m'adapter au plus grand pic, mais je ne peux pas m'adapter au plus petit pic. Je comprends que j'ai besoin de résumer la fonction gaussienne pour les deux pics, mais je ne sais pas où je me suis trompé. Une image de ma sortie actuelle est affichée:
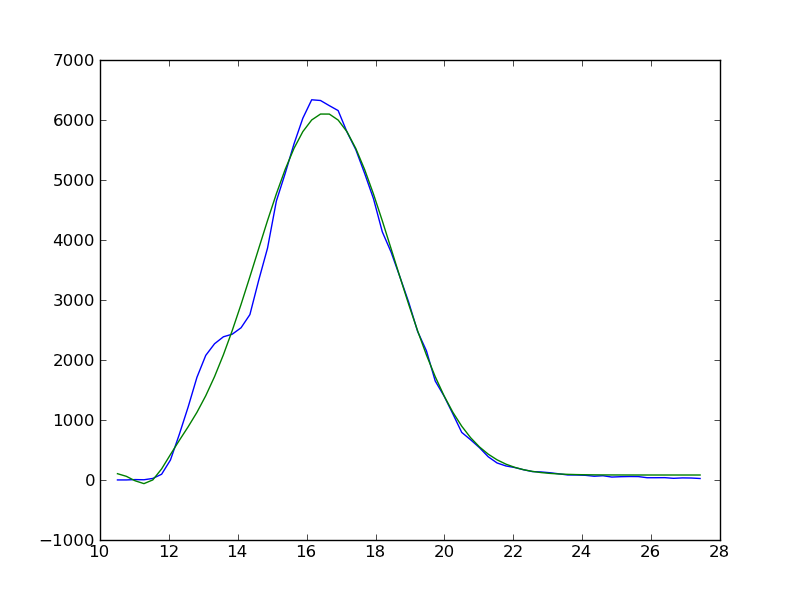
La ligne bleue est mes données et la ligne verte est mon ajustement. Il y a un Epaule à gauche du pic principal de mes données que j'essaie actuellement d'ajuster, en utilisant le code suivant:
import matplotlib.pyplot as pt
import numpy as np
from scipy.optimize import leastsq
from pylab import *
time = []
counts = []
for i in open('/some/folder/to/file.txt', 'r'):
segs = i.split()
time.append(float(segs[0]))
counts.append(segs[1])
time_array = arange(len(time), dtype=float)
counts_array = arange(len(counts))
time_array[0:] = time
counts_array[0:] = counts
def model(time_array0, coeffs0):
a = coeffs0[0] + coeffs0[1] * np.exp( - ((time_array0-coeffs0[2])/coeffs0[3])**2 )
b = coeffs0[4] + coeffs0[5] * np.exp( - ((time_array0-coeffs0[6])/coeffs0[7])**2 )
c = a+b
return c
def residuals(coeffs, counts_array, time_array):
return counts_array - model(time_array, coeffs)
# 0 = baseline, 1 = amplitude, 2 = centre, 3 = width
peak1 = np.array([0,6337,16.2,4.47,0,2300,13.5,2], dtype=float)
#peak2 = np.array([0,2300,13.5,2], dtype=float)
x, flag = leastsq(residuals, peak1, args=(counts_array, time_array))
#z, flag = leastsq(residuals, peak2, args=(counts_array, time_array))
plt.plot(time_array, counts_array)
plt.plot(time_array, model(time_array, x), color = 'g')
#plt.plot(time_array, model(time_array, z), color = 'r')
plt.show()
3 réponses
ce code a fonctionné pour moi à condition que vous ne positionniez qu'une fonction qui est une combinaison de deux distributions gaussiennes.
je viens de faire une fonction de résidus qui ajoute deux fonctions gaussiennes et puis les soustrait des données réelles.
les paramètres (p) que j'ai passés à la fonction des moindres carrés de Numpy comprennent: la moyenne de la première fonction gaussienne (m), la différence de la moyenne de la première et de la deuxième fonctions gaussienne (dm, c.-à-d. l'horizontale maj), l'écart-type de la première (sd1), et l'écart-type de la deuxième (sd2).
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
######################################
# Setting up test data
def norm(x, mean, sd):
norm = []
for i in range(x.size):
norm += [1.0/(sd*np.sqrt(2*np.pi))*np.exp(-(x[i] - mean)**2/(2*sd**2))]
return np.array(norm)
mean1, mean2 = 0, -2
std1, std2 = 0.5, 1
x = np.linspace(-20, 20, 500)
y_real = norm(x, mean1, std1) + norm(x, mean2, std2)
######################################
# Solving
m, dm, sd1, sd2 = [5, 10, 1, 1]
p = [m, dm, sd1, sd2] # Initial guesses for leastsq
y_init = norm(x, m, sd1) + norm(x, m + dm, sd2) # For final comparison plot
def res(p, y, x):
m, dm, sd1, sd2 = p
m1 = m
m2 = m1 + dm
y_fit = norm(x, m1, sd1) + norm(x, m2, sd2)
err = y - y_fit
return err
plsq = leastsq(res, p, args = (y_real, x))
y_est = norm(x, plsq[0][0], plsq[0][2]) + norm(x, plsq[0][0] + plsq[0][1], plsq[0][3])
plt.plot(x, y_real, label='Real Data')
plt.plot(x, y_init, 'r.', label='Starting Guess')
plt.plot(x, y_est, 'g.', label='Fitted')
plt.legend()
plt.show()
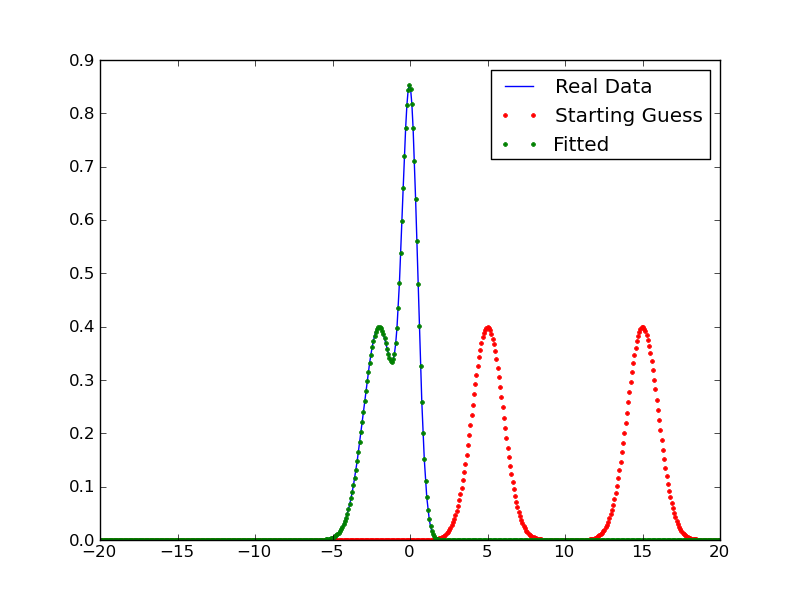
vous pouvez utiliser des modèles de mélange gaussien de scikit-learn:
from sklearn import mixture
import matplotlib.pyplot
import matplotlib.mlab
import numpy as np
clf = mixture.GMM(n_components=2, covariance_type='full')
clf.fit(yourdata)
m1, m2 = clf.means_
w1, w2 = clf.weights_
c1, c2 = clf.covars_
histdist = matplotlib.pyplot.hist(yourdata, 100, normed=True)
plotgauss1 = lambda x: plot(x,w1*matplotlib.mlab.normpdf(x,m1,np.sqrt(c1))[0], linewidth=3)
plotgauss2 = lambda x: plot(x,w2*matplotlib.mlab.normpdf(x,m2,np.sqrt(c2))[0], linewidth=3)
plotgauss1(histdist[1])
plotgauss2(histdist[1])
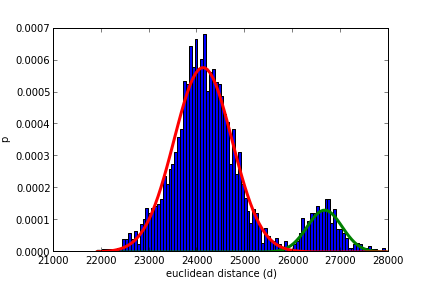
vous pouvez aussi utiliser la fonction ci-dessous pour ajuster le nombre de gaussiens que vous voulez avec le paramètre ncomp:
from sklearn import mixture
%pylab
def fit_mixture(data, ncomp=2, doplot=False):
clf = mixture.GMM(n_components=ncomp, covariance_type='full')
clf.fit(data)
ml = clf.means_
wl = clf.weights_
cl = clf.covars_
ms = [m[0] for m in ml]
cs = [numpy.sqrt(c[0][0]) for c in cl]
ws = [w for w in wl]
if doplot == True:
histo = hist(data, 200, normed=True)
for w, m, c in zip(ws, ms, cs):
plot(histo[1],w*matplotlib.mlab.normpdf(histo[1],m,np.sqrt(c)), linewidth=3)
return ms, cs, ws
les coefficients 0 et 4 sont dégénérés - il n'y a absolument rien dans les données qui puisse décider entre eux. vous devez utiliser un seul paramètre de niveau zéro au lieu de deux (c'est-à-dire supprimer l'un d'eux de votre code). c'est probablement ce qui arrête votre ajustement (ignorez les commentaires ici disant que ce n'est pas possible - il y a clairement au moins deux pics dans ces données et vous devriez certainement être en mesure de s'adapter à cela).
(il peut ne pas être clair pourquoi je suggère, mais ce qui se passe est-ce que les coefficients 0 et 4 peuvent s'annuler mutuellement. ils peuvent tous les deux être zéro, ou l'un pourrait être 100 et l'autre -100 - dans tous les cas, l'ajustement est tout aussi bon. cela "confond" la routine appropriée, qui passe son temps à essayer de déterminer ce qu'ils devraient être, quand il n'y a pas de réponse unique, parce que quelle que soit la valeur de l'un, l'autre peut être juste le négatif de cela, et l'ajustement sera le même).
en fait, de l'intrigue, on dirait qu'il ya peut-être pas besoin d'un niveau zéro à tous. j'essaierais de laisser tomber les deux et de voir à quoi ressemble la forme.