Python: filtre bandpass d'une image

j'ai une image de données avec un artefact d'imagerie qui sort comme un fond sinusoïdal, que je veux enlever. Comme il s'agit d'une onde sinusoïdale à fréquence simple, il semble naturel de transformer de Fourier et soit filtre bandpass ou "filtre notch" (où je pense que je voudrais utiliser un filtre gaussien à +-omega).

essayez de faire cela, je remarque deux choses:

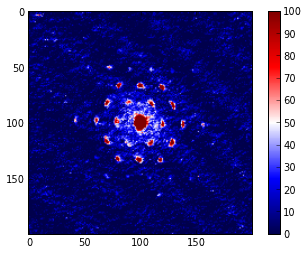
1) simplement en effectuant le fft et retour, j'ai réduit le sine vague composant, illustré ci-dessous. On dirait qu'il y a un filtrage des données en haut lieu juste en allant là-bas et en revenant?

import numpy as np

f = np.fft.fft2(img)                  #do the fourier transform
fshift1 = np.fft.fftshift(f)          #shift the zero to the center
f_ishift = np.fft.ifftshift(fshift1)  #inverse shift
img_back = np.fft.ifft2(f_ishift)     #inverse fourier transform
img_back = np.abs(img_back)

C'est une image de img_back:

peut-être que le filtrage ici est assez bon pour moi, mais je n'en suis pas si sûr puisque je n'ai pas une bonne compréhension de la suppression de l'arrière-plan.

2) pour être plus sûr de la suppression aux fréquences indésirables, j'ai fait un booléen 'bandpass' masque et l'a appliqué aux données, mais la Transformée de fourier ignore le masque.

a = shape(fshift1)[0]
b = shape(fshift1)[1]

ro = 8
ri = 5
y,x = np.ogrid[-a/2:a/2, -b/2:b/2] 
m1 = x*x + y*y >= ro*ro 
m2 = x*x + y*y <= ri*ri
m3=np.dstack((m1,m2))       
maskcomb =[]
for r in m3:
    maskcomb.append([any(c) for c in r])  #probably not pythonic, sorry
newma = np.invert(maskcomb)
filtdat = ma.array(fshift1,mask=newma) 
imshow(abs(filtdat))
f_ishift = np.fft.ifftshift(filtdat) 
img_back2 = np.fft.ifft2(f_ishift) 
img_back2 = np.abs(img_back2)

Ici, le résultat est le même qu'avant, parce que np.fft ignore les masques. La correction est simple:

filtdat2 = filtdat.filled(filtdat.mean())

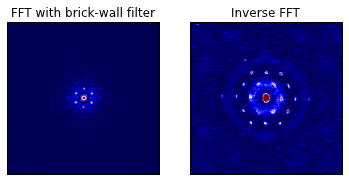
malheureusement, (mais à la réflexion aussi sans surprise) le résultat est montré ici:

le tracé de gauche est celui de l'amplitude du FFT, avec le filtre bandpass appliqué. Il est l'anneau sombre autour du composant central (DC). La phase n'est pas montrée.

de toute évidence, le filtre' brickwall ' n'est pas la bonne solution. Le phénomène de fabrication d'anneaux à partir de ce filtre est bien expliqué ici:Ce qui se passe lorsque vous appliquez une brique de mur filtre à 1D dataset.

alors maintenant je suis coincé. Peut-être serait-il préférable d'utiliser l'une des méthodes construites dans scipy, mais elles semblent être pour les données 1d, comme dans cette implémentation d'un butterworth filtre. Peut-être que la bonne chose à faire est d'utiliser fftconvolve() comme c'est fait ici pour brouiller une image. ma question à propos de fftconvolve est la suivante: est-ce qu'il faut que les 'images' (l'image et le filtre) soient dans l'espace réel? Je pense que oui, mais dans l'exemple ils utilisent une gaussienne, il est donc ambigu (fft(gaussien)=gaussienne). Si oui, alors il semble erroné d'essayer de faire un véritable espace de filtre passe-bande. Peut-être que la bonne stratégie utilise convolve2d() avec l'image spatiale de fourier et un filtre maison. Si oui, savez-vous comment faire une bonne 2d filtre?