Interpolation linéaire Python 4D sur une grille rectangulaire
j'ai besoin d'interpoler linéairement les données de température en 4 dimensions (latitude, longitude, altitude et temps).
Le nombre de points est assez élevé (360x720x50x8) et j'ai besoin d'une méthode rapide pour calculer la température à n'importe quel point dans l'espace et le temps dans les limites des données.
j'ai essayé d'utiliser scipy.interpolate.LinearNDInterpolator mais l'utilisation de Qhull pour la triangulation est inefficace sur une grille rectangulaire et prend des heures à compléter.
en lisant ceci SciPy billet, la solution semblait être de mettre en place un nouvel interpolateur nd en utilisant la norme interp1d pour calculer un plus grand nombre de points de données, puis utiliser une approche de "voisin le plus proche" avec le nouvel ensemble de données.
cela, cependant, prend encore beaucoup de temps (minutes).
Existe-t-il un moyen rapide d'interpoler des données sur une grille rectangulaire en 4 dimensions sans que cela prenne des minutes à accomplir?
j'ai pensé à l'aide de interp1d 4 fois sans calculant une densité plus élevée de points, mais laissant à l'utilisateur le soin d'appeler avec les coordonnées, mais je n'arrive pas à savoir comment faire cela.
sinon, Est-ce que l'écriture de mon propre interpolateur 4D spécifique à mes besoins serait une option ici?
Voici le code que j'ai utilisé pour tester ceci:
en utilisant scipy.interpolate.LinearNDInterpolator:
import numpy as np
from scipy.interpolate import LinearNDInterpolator
lats = np.arange(-90,90.5,0.5)
lons = np.arange(-180,180,0.5)
alts = np.arange(1,1000,21.717)
time = np.arange(8)
data = np.random.rand(len(lats)*len(lons)*len(alts)*len(time)).reshape((len(lats),len(lons),len(alts),len(time)))
coords = np.zeros((len(lats),len(lons),len(alts),len(time),4))
coords[...,0] = lats.reshape((len(lats),1,1,1))
coords[...,1] = lons.reshape((1,len(lons),1,1))
coords[...,2] = alts.reshape((1,1,len(alts),1))
coords[...,3] = time.reshape((1,1,1,len(time)))
coords = coords.reshape((data.size,4))
interpolatedData = LinearNDInterpolator(coords,data)
en utilisant scipy.interpolate.interp1d:
import numpy as np
from scipy.interpolate import LinearNDInterpolator
lats = np.arange(-90,90.5,0.5)
lons = np.arange(-180,180,0.5)
alts = np.arange(1,1000,21.717)
time = np.arange(8)
data = np.random.rand(len(lats)*len(lons)*len(alts)*len(time)).reshape((len(lats),len(lons),len(alts),len(time)))
interpolatedData = np.array([None, None, None, None])
interpolatedData[0] = interp1d(lats,data,axis=0)
interpolatedData[1] = interp1d(lons,data,axis=1)
interpolatedData[2] = interp1d(alts,data,axis=2)
interpolatedData[3] = interp1d(time,data,axis=3)
je vous Remercie beaucoup pour votre aide!
3 réponses
dans le même ticket que vous avez lié, il y a un exemple d'implémentation de ce qu'ils appellent interpolation du produit tenseur, montrant la bonne façon de nid d'appels récursifs à interp1d. Ceci est équivalent à une interpolation quadrilinéaire si vous choisissez la valeur par défaut kind='linear' paramètre interp1d.
bien que cela puisse être suffisant, ce n'est pas une interpolation linéaire, et il y aura des termes d'ordre plus élevé dans la fonction d'interpolation, comme cette image de la entrée de wikipedia sur la méthode d'interpolation bilinéaire affiche:
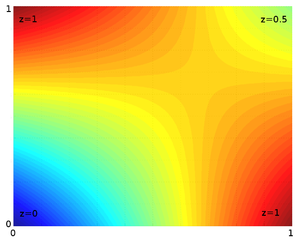
cela peut très bien être suffisant pour ce que vous recherchez, mais il y a des applications où une interpoaltion triangulée, vraiment linéaire par morceaux, est préférée. Si vous avez vraiment besoin de cela, il ya un moyen facile de contourner la lenteur de qhull.
une Fois LinearNDInterpolator a été configuré, il y a deux étapes pour arriver à une valeur interpolée pour une donnée point:
- trouvez à l'intérieur de quel triangle (hypertétraèdre 4D dans votre cas) le point est, et
- interpoler en utilisant le coordonnées barycentriques du point relatif aux sommets comme poids.
vous ne voulez probablement pas jouer avec les coordonnées barycentriques, alors mieux vaut laisser cela à LinearNDInterpolator. Mais vous savez des choses sur la triangulation. Surtout ça, parce que vous avez une grille régulière, à l'intérieur de chaque hypercube la triangulation sera la même. Donc pour interpoler une seule valeur, vous pourriez d'abord déterminer dans quel subcube votre point est, construire un LinearNDInterpolator avec les 16 sommets de ce cube, et utilisez - le pour interpoler votre valeur:
from itertools import product
def interpolator(coords, data, point) :
dims = len(point)
indices = []
sub_coords = []
for j in xrange(dims) :
idx = np.digitize([point[j]], coords[j])[0]
indices += [[idx - 1, idx]]
sub_coords += [coords[j][indices[-1]]]
indices = np.array([j for j in product(*indices)])
sub_coords = np.array([j for j in product(*sub_coords)])
sub_data = data[list(np.swapaxes(indices, 0, 1))]
li = LinearNDInterpolator(sub_coords, sub_data)
return li([point])[0]
>>> point = np.array([12.3,-4.2, 500.5, 2.5])
>>> interpolator((lats, lons, alts, time), data, point)
0.386082399091
cela ne peut pas fonctionner sur des données vectorisées, puisque cela nécessiterait de stocker un LinearNDInterpolator pour chaque subcube possible, et même s'il serait probablement plus rapide que la triangulation de l'ensemble, il serait encore très lent.
scipy.ndimage.map_coordinates est un interpolateur rapide agréable pour les grilles uniformes (toutes les boîtes de la même taille). Voir multivariée-spline interpolation-en-python-scipy DONC pour une description claire.
pour les grilles rectangulaires non uniformes, une enveloppe simple Maillage cartes / échelles non uniformes aux grilles uniformes, puis map_coordinates. Sur un cas de test 4d comme le vôtre, il faut environ 1 µsec par requête:
Intergrid: 1000000 points in a (361, 720, 47, 8) grid took 652 msec
Pour des choses similaires-je utiliser Scientifique.Fonction.Interpolation.InterpolatingFunction.
import numpy as np
from Scientific.Functions.Interpolation import InterpolatingFunction
lats = np.arange(-90,90.5,0.5)
lons = np.arange(-180,180,0.5)
alts = np.arange(1,1000,21.717)
time = np.arange(8)
data = np.random.rand(len(lats)*len(lons)*len(alts)*len(time)).reshape((len(lats),len(lons),len(alts),len(time)))
axes = (lats, lons, alts, time)
f = InterpolatingFunction(axes, data)
Vous pouvez désormais laisser à l'utilisateur d'appeler le InterpolatingFunction avec les coordonnées:
>>> f(0,0,10,3)
0.7085675631375401
InterpolatingFunction possède de jolies fonctionnalités supplémentaires, telles que l'intégration et le tranchage.
Cependant, je ne sais pas si l'interpolation est linéaire. Il faudrait chercher dans le module source pour le savoir.