Python: Tracé de contour 2d à partir de 3 listes: x, Y et rho?
J'ai un problème simple en python et matplotlib. J'ai 3 listes : x, y et rho avec rho[i] une densité au point x[i], y[i]. Toutes les valeurs de x et y sont comprises entre -1. et 1. mais ils ne sont pas dans un ordre spécifique.
Comment faire un tracé de contour (comme avec imshow) de la densité rho (interpolée aux points x, y).
Merci beaucoup.
EDIT: je travaille avec de grands tableaux: x, Y et rho ont entre 10 000 et 1 000 000 d'éléments
2 réponses
Vous devez interpoler vos valeurs rho. Il n'y a pas une seule façon de le faire, et la "meilleure" méthode dépend entièrement de l'information a priori que vous devriez incorporer dans l'interpolation.
Avant d'aller dans une diatribe sur les méthodes d'interpolation "boîte noire", cependant, une fonction de base radiale (par exemple, une "plaque mince-spline" est un type particulier de fonction de base radiale) est souvent un bon choix. Si vous avez des millions de points, cette mise en œuvre sera inefficace, mais comme un départ point:
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate
# Generate data:
x, y, z = 10 * np.random.random((3,10))
# Set up a regular grid of interpolation points
xi, yi = np.linspace(x.min(), x.max(), 100), np.linspace(y.min(), y.max(), 100)
xi, yi = np.meshgrid(xi, yi)
# Interpolate
rbf = scipy.interpolate.Rbf(x, y, z, function='linear')
zi = rbf(xi, yi)
plt.imshow(zi, vmin=z.min(), vmax=z.max(), origin='lower',
extent=[x.min(), x.max(), y.min(), y.max()])
plt.scatter(x, y, c=z)
plt.colorbar()
plt.show()
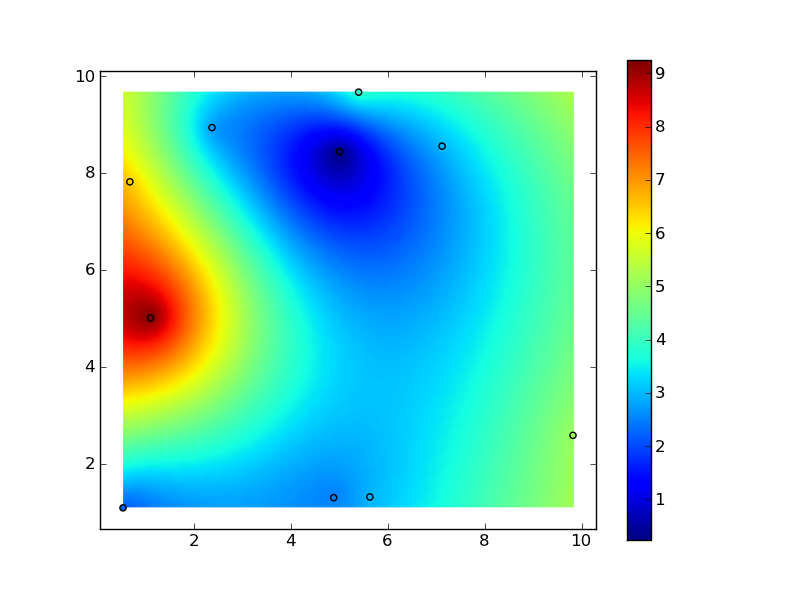
Vous pouvez utiliser griddata de scipy (nécessite Scipy >= 0.10), c'est une méthode basée sur la triangulation.
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate
# Generate data: for N=1e6, the triangulation hogs 1 GB of memory
N = 1000000
x, y = 10 * np.random.random((2, N))
rho = np.sin(3*x) + np.cos(7*y)**3
# Set up a regular grid of interpolation points
xi, yi = np.linspace(x.min(), x.max(), 300), np.linspace(y.min(), y.max(), 300)
xi, yi = np.meshgrid(xi, yi)
# Interpolate; there's also method='cubic' for 2-D data such as here
zi = scipy.interpolate.griddata((x, y), rho, (xi, yi), method='linear')
plt.imshow(zi, vmin=rho.min(), vmax=rho.max(), origin='lower',
extent=[x.min(), x.max(), y.min(), y.max()])
plt.colorbar()
plt.show()
Il y a aussi une interpolation à distance pesée inverse-similaire à RBF, mais devrait mieux fonctionner pour un grand nombre de points: Interpolation à Distance pondérée Inverse (IDW) avec Python