j'ai une liste de n observations, dont chacune est la somme de deux variables distribuées par Weibull:

x[i] = t1[i] + t2[i]
t1[i] ~ Weibull(shape1, scale1)
t2[i] ~ Weibull(shape2, scale2)

mon but est:

1) estimer les paramètres de forme et d'échelle pour les deux distributions de Weibull (shape1, scale1, shape2, scale2),

2) pour chaque observation x[i], l'estimation t1[i] (et t2[i] en découle).

( Mis À Part: Chaque l'observation x [i] est l'âge du diagnostic de cancer, et t1[i] et t2[i] sont deux périodes différentes dans le développement de la tumeur. Le modèle actuel implique des données de mutation, mais avant j'ai essayer ça, je veux m'assurer que je peux utiliser PyMC pour ce simple problème.)

J'utilise PyMC2 pour faire ces estimations, et il semble que la course converge, mais à des résultats incorrects. Je ne sais pas s'il y a un problème avec ma syntaxe de modèle PyMC, avec le MCMC les paramètres, ou les deux. J'ai essayé d'adapter ce conseil sur l'utilisation des potentiels pour modéliser les variables latentes. D'abord, je définis x[i] et t1[i] pour chaque observation:

for i in xrange(n):
    x[i] = pm.Index('x_%i'%i, x=data, index=i) # data is a list of observations
    t1[i] = pm.Weibull('t1_%i'%i, alpha=shape1, beta=scale1)
    # Ensure that initial guess for t1 is not more than the observed sum:
    if t1[i].value >= x[i].value:
        t1[i].value = 0.95 * x[i].value

ensuite je définis un déterministe pour t2 [i] = x[i] - t1 [I]:

for i in xrange(n):
    def subtractfunc(t1=t1, x=x, ii=i):
        return x[ii] - t1[ii]
    t2[i] = pm.Lambda('t2_%i'%i, subtractfunc)

et dernier je définit le potentiel pour t2 [i]:

t2dist = np.empty(n, dtype=object)
for i in xrange(n):
    def weibfunc(t2=t2, shape2=shape2, scale2=scale2, ii=i):
        return pm.weibull_like(t2[ii], alpha=shape2, beta=scale2)
    t2dist[i] = pm.Potential(logp = weibfunc,
                               name = 't2dist_%i'%i,
                               parents = {'shape2':shape2, 'scale2':scale2, 't2':t2},
                               doc = 'weibull potential for t2',
                               verbose = 0,
                               cache_depth = 2)

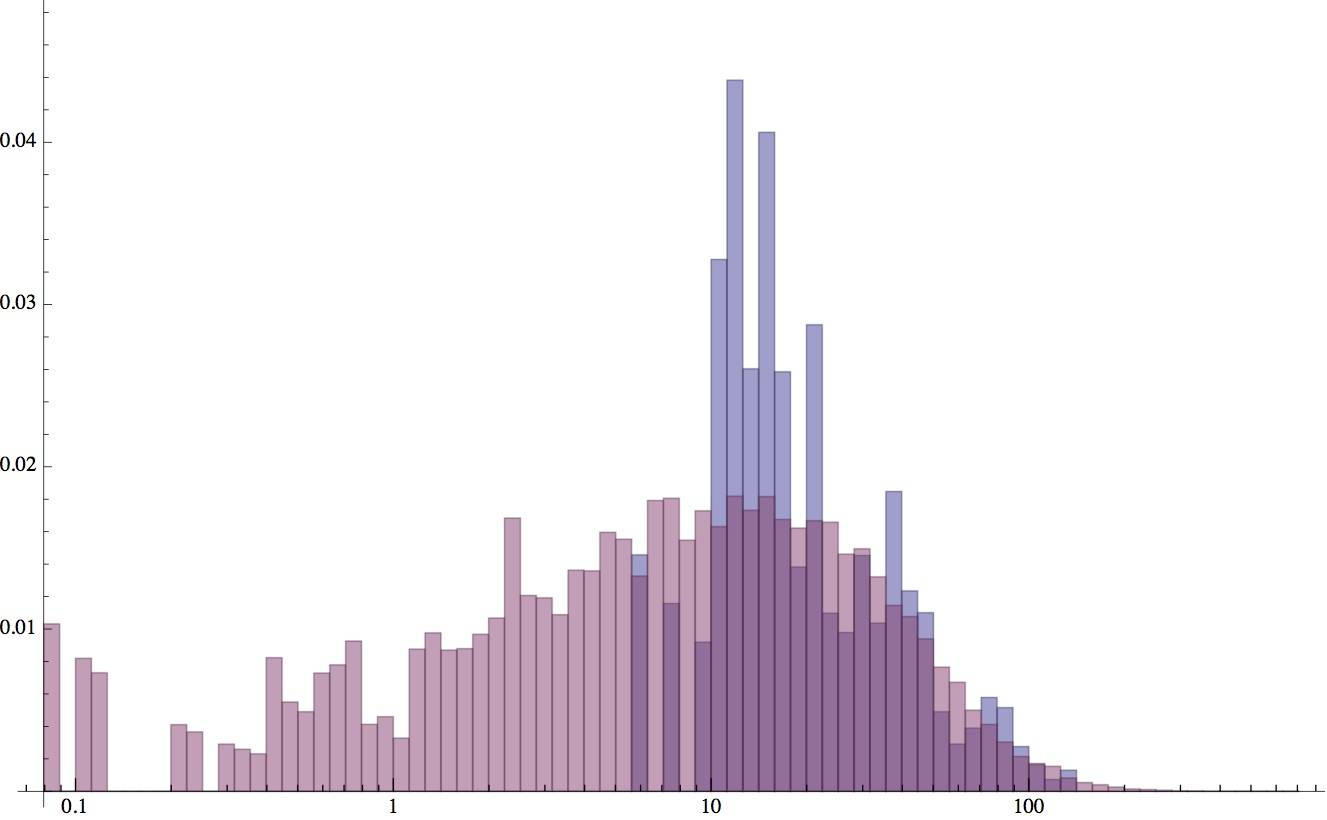
vous pouvez voir mon code complet ici . je teste par la simulation de 60 observations indépendantes, avec shape1 = 1, échelle1 = 30, shape2 = 6.5, échelle2 = 10, et je 1e5 itérations de AdaptiveMetropolis. Les résultats convergent pour une moyenne de shape1=1.94, échelle1=37.9, shape2=0.55, échelle2=36.1, et l'ic à 95% Pa ne comprennent pas les vraies valeurs. Cette distribution résultante n'est même pas dans la sphère droite, comme cet histogramme montre. (Le bleu montre les données simulées x[i] que j'ai utilisées, tandis que le rouge montre le complètement différent inféré distribution à partir d'une itération représentative dans la course MCMC.)

Exécutant de nouveau avec une autre graine aléatoire, je reçois shape1=4.65, échelle1=23.3, shape2=0.83, échelle2=21.3. Cette répartition est un peu plus proche de la vérité. Y a-t-il un moyen de modifier les paramètres de la CMCM pour obtenir des résultats décents pour ce genre de problème? Tout conseil sur L'utilisation plus efficace de PyMC est très apprécié.

mise à jour -- essayé un" assisté "course MCMC:

j'ai aussi essayé d'aider le CMCM en initialisant les paramètres au niveau de la population avec des valeurs proches de la vérité. Les résultats sont un peu meilleurs, mais je constate maintenant un biais systématique. L'histogramme ci-dessous montre la distribution réelle des observations (bleu) par rapport à la distribution ajustée (rouge). La queue droite s'ajuste bien, mais l'ajustement ne parvient pas à capturer le sommet pointu du côté gauche. Ce biais est constant pour les tailles de population n = 60 et 100. Je ne suis pas sûr si ce n'est plus un Question de cymp ou Problème général d'algorithme de MCMC.