Placez N cercles de rayons différents à l'intérieur d'un cercle plus grand sans chevauchement
Étant donné n cercles avec des rayons r1 ... rn, positionnez-les de manière à ce qu'aucun cercle ne se chevauche et que le cercle de délimitation soit de" petit " rayon.
Le programme prend une liste [r1, r2, ... rn] comme entrée et sorties les centres des cercles.
- je demande "petit "parce que le rayon" minimum " le convertit en un problème beaucoup plus difficile (la version minimale a déjà été prouvée comme NP hard/complete - voir la note de bas de page près de la fin de la question). Nous n'avons pas besoin au minimum. Si l' la forme faite par les cercles semble être assez circulaire, c'est assez bon.
- Vous pouvez supposer que Rmax / Rmin
- une préoccupation de faible priorité - le programme devrait être capable de gérer plus de 2000 cercles. Au début, même 100-200 cercles devraient être bien.
- Vous avez peut-être deviné que les cercles n'ont pas besoin d'être serrés ou même de se toucher.
Le but est de trouver un arrangement visuellement agréable des cercles donnés qui peuvent s'adapter à l'intérieur d'un cercle plus grand et ne pas laisser trop d'espace vide. (comme les cercles dans une image de test de daltonisme ).
Vous pouvez utiliser le code Python ci-dessous comme point de départ (vous auriez besoin de numpy et matplotlib pour ce code - "sudo apt-get install numpy matplotlib" sur linux)...
import pylab
from matplotlib.patches import Circle
from random import gauss, randint
from colorsys import hsv_to_rgb
def plotCircles(circles):
# input is list of circles
# each circle is a tuple of the form (x, y, r)
ax = pylab.figure()
bx = pylab.gca()
rs = [x[2] for x in circles]
maxr = max(rs)
minr = min(rs)
hue = lambda inc: pow(float(inc - minr)/(1.02*(maxr - minr)), 3)
for circle in circles:
circ = Circle((circle[0], circle[1]), circle[2])
color = hsv_to_rgb(hue(circle[2]), 1, 1)
circ.set_color(color)
circ.set_edgecolor(color)
bx.add_patch(circ)
pylab.axis('scaled')
pylab.show()
def positionCircles(rn):
# You need rewrite this function
# As of now, this is a dummy function
# which positions the circles randomly
maxr = int(max(rn)/2)
numc = len(rn)
scale = int(pow(numc, 0.5))
maxr = scale*maxr
circles = [(randint(-maxr, maxr), randint(-maxr, maxr), r)
for r in rn]
return circles
if __name__ == '__main__':
minrad, maxrad = (3, 5)
numCircles = 400
rn = [((maxrad-minrad)*gauss(0,1) + minrad) for x in range(numCircles)]
circles = positionCircles(rn)
plotCircles(circles)
Ajout d'informations: l'algorithme d'emballage de cercle couramment mentionné dans les résultats de recherche google ne s'applique pas à ce problème.
L'énoncé du problème de L'autre" algorithme D'empaquetage de cercle " est donc : étant donné un complexe k (les graphes dans ce contexte sont appelés complexes simpliciaux, ou complexes en bref) et des conditions aux limites appropriées, calculer les rayons de l'empaquetage de cercle correspondant pour K....
Il commence essentiellement à partir d'un graphique indiquant quels cercles se touchent (les sommets du graphique désignent les cercles, et les bords indiquent la relation tactile/tangentielle entre les cercles). Il faut trouver les rayons du cercle et les positions de manière à satisfaire la relation touchante dénotée par le graphique.
L'autre problème a une observation intéressante (indépendante de ce problème):
Théorème D'emballage de cercle - chaque emballage de cercle a un graphe planaire correspondant (c'est la partie facile/évidente), et chaque graphe planaire a un emballage de cercle correspondant (la partie pas si évidente). Les graphiques et les emballages sont duaux les uns des autres et sont uniques.
Nous n'avons pas de graphe planaire ou tangentiel relation pour commencer à partir de notre problème.
Cet article - Robert J. Fowler, Mike Paterson, Steven L. Tanimoto: L'emballage Optimal et la couverture dans l'avion sont NP-Complete - prouve que la version minimale de ce problème est NP-complete. Cependant, le document n'est pas disponible en ligne (du moins pas facilement).
6 réponses
J'ai un passage assez naïf (sur les rayons) solution qui produit des résultats corrects, bien qu'il y ait certainement place à l'amélioration. J'ai quelques idées dans cette direction, mais je pourrais aussi bien partager ce que j'ai au cas où quelqu'un d'autre voudrait le pirater aussi.
On dirait qu'ils se croisent au centre, mais ils ne le font pas. j'ai décoré la fonction de placement avec une boucle imbriquée qui vérifie chaque cercle contre chaque autre cercle (deux fois) et soulève un AssertionError s'il y a une intersection.
En outre, je peux obtenir le bord proche de la perfection en inversant simplement le tri de la liste mais je ne pense pas que le centre semble bon de cette façon. C'est (à peu près la seule chose ;) discuté dans les commentaires au code.
L'idée est de ne regarder que les points discrets sur lesquels un cercle peut vivre et de les parcourir en utilisant le générateur suivant:
def base_points(radial_res, angular_res):
circle_angle = 2 * math.pi
r = 0
while 1:
theta = 0
while theta <= circle_angle:
yield (r * math.cos(theta), r * math.sin(theta))
r_ = math.sqrt(r) if r > 1 else 1
theta += angular_res/r_
r += radial_res
Cela commence juste à l'origine et trace des points le long de cercles concentriques autour d'elle. Nous traiter les rayons en les triant selon certains paramètres pour garder les grands cercles près du centre (début de liste) mais assez petits près du début pour remplir les espaces. Nous itérons ensuite sur les rayons. dans la boucle principale, nous faisons d'abord une boucle sur les points que nous avons déjà examinés et sauvegardés. Si aucun de ceux-ci ne convient, nous commençons à extraire de nouveaux points du générateur et à les enregistrer (dans l'ordre) jusqu'à ce que nous trouvions un endroit approprié. Nous plaçons ensuite le cercle et parcourons notre liste des points enregistrés tirant sur tous ceux qui tombent dans le nouveau cercle. Nous répétons ensuite. sur le prochain rayon.
Je vais mettre quelques idées que j'ai en jeu et en faire mo'bettah. Cela pourrait servir de bonne première étape pour une idée basée sur la physique parce que vous commencez sans chevauchement. Bien sûr, il pourrait déjà être assez serré pour que vous n'auriez pas beaucoup de place.
Aussi, je n'ai jamais joué avec numpy ou matplotlib donc j'écris juste vanilla python. Il y a peut être quelque chose là dedans cela le fera courir beaucoup plus vite, je vais devoir regarder.
Pas une solution, juste une idée de remue-méninges: IIRC une façon courante d'obtenir des solutions approximatives au TSP est de commencer par une configuration aléatoire, puis d'appliquer des opérations locales (par exemple "échanger" deux bords dans le chemin) pour essayer d'obtenir des chemins de plus en plus courts. (lien Wikipédia)
Je pense que quelque chose de similaire serait possible ici:
- commencez par des positions au centre aléatoires
- "optimiser" ces positions, donc il n'y a pas de cercles qui se chevauchent et donc le les cercles sont aussi proches que possible, en augmentant la distance entre les cercles qui se chevauchent et en diminuant la distance entre les autres cercles, jusqu'à ce qu'ils soient serrés. Cela pourrait être fait par une sorte de minimisation de l'énergie, ou il pourrait être plus efficace gourmand solution.
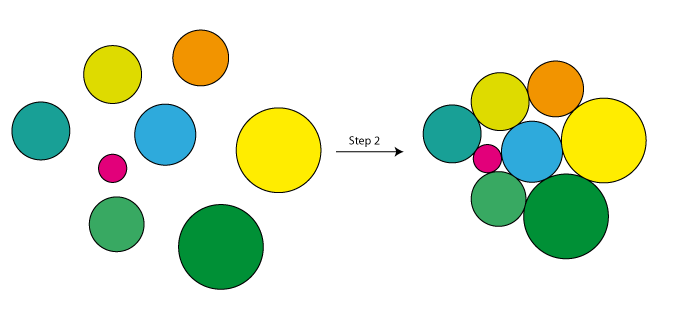
- appliquer un opérateur d'amélioration itérative aux positions centrales
- Goto 2, pause après un nombre maximum d'itérations ou si la dernière itération n'a trouvé aucune amélioration
Le la question intéressante est la suivante: quel type d ' "opérateur d'amélioration itérative" pourriez-vous utiliser à l'étape 3? Nous pouvons supposer que les positions à ce stade sontlocalement optimales, mais elles pourraient être améliorées en réarrangeant une grande fraction des cercles. Ma suggestion serait de choisir arbitrairement une ligne à travers les cercles. Ensuite, prenez tous les cercles "à gauche" de la ligne et réfléchissez-les à un axe perpendiculaire à cette ligne:
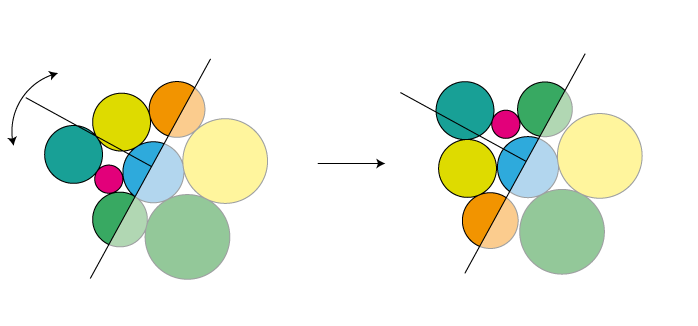Vous essayez probablement plusieurs lignes et choisissez celle qui mène à la solution la plus compacte.
L'idée est, si certains des cercles sont déjà à ou près de leur configuration optimale, les chances sont bonnes cette opération ne les dérangera pas.
Autres opérations possibles auxquelles je pourrais penser:
- prenez l'un des cercles avec la plus grande distance du centre (l'un touchant le cercle limite), et déplacez-le au hasard ailleurs:
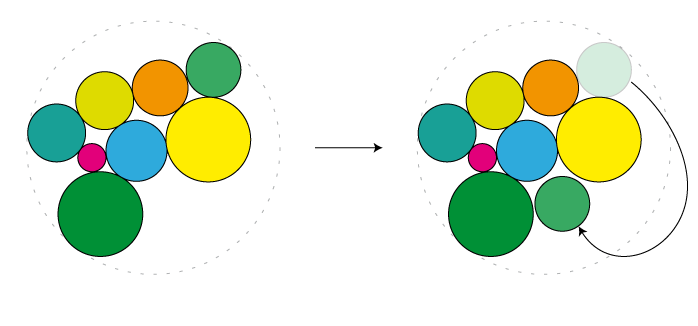
- Choisissez un ensemble de cercles proches les uns des autres (par exemple, si leurs centres un cercle choisi au hasard) et les faire pivoter par un angle aléatoire.
- une autre option (bien qu'un peu plus complexe) serait de mesurer la surface entre les cercles, quand ils sont serrés:
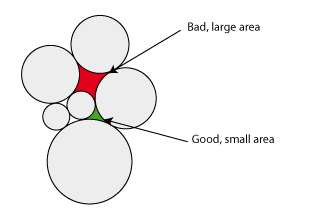
Ensuite, vous pouvez choisir l'un des cercles adjacents à la plus grande zone entre les cercles (la zone rouge, dans l'image) et l'échanger avec un autre cercle, ou le déplacer quelque part vers la limite.
(réponse au commentaire:) notez que chacune de ces "améliorations" est presque garanti pour créer des chevauchements et / ou un espace inutile entre les cercles. Mais dans la prochaine itération, l'étape 2 déplacera les cercles afin qu'ils soient étroitement emballés et ne se chevauchent pas à nouveau. De cette façon, je peux avoir une étape pour les optimisations locales (sans me soucier des optimisations globales), et une étape pour les optimisations globales (qui pourraient créer localement des solutions sous-optimales). C'est beaucoup plus facile que d'avoir une étape complexe qui fait les deux.
Pouvez-vous traiter les cercles comme des particules chargées dans une cavité chargée et rechercher une solution stable? C'est-à-dire que les cercles se repoussent en fonction de la proximité, mais sont attirés vers l'origine. Quelques étapes de simulation pourraient vous obtenir une réponse décente.
Sonne comme un problème D'emballage de cercle, voici quelques informations:
Http://en.wikipedia.org/wiki/Apollonian_gasket
Cela semble quelque peu de ce que vous essayez de faire, et peut fournir des contraintes potentielles pour vous.
Vous pouvez essayer d'utiliser une bibliothèque de physique 2d, et simplement verser vos cercles 2d dans un conteneur circulaire plus grand - et attendre qu'ils se mettent en place.