Tracé des lignes horizontales et verticales dans Mathematica

Si vous êtes réellement en utilisant Complot (ou ListPlot, et c.), la solution la plus simple est d'utiliser le Quadrillage option, qui vous permet de spécifier le x et o - valeurs où vous voulez que les lignes soient dessinées. Par exemple:

Plot[Sin[x], {x, 0, 2 \[Pi]},
  GridLines -> {{0, \[Pi]/2, \[Pi], 3 \[Pi]/2, 2 \[Pi]},
                {-1, -Sqrt[3]/2, -1/2, 0, 1/2, Sqrt[3]/2, 1}}]

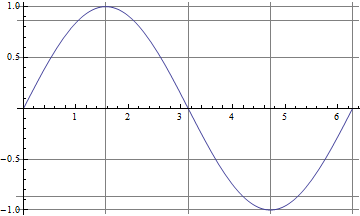
EDIT pour ajouter:

bien sûr, cette solution fonctionne si vous voulez simplement tracer une ligne à un numéro donné. Pour exemple, si vous souhaitez reproduire le deuxième exemple dreeve réponse:

Plot[Sin[x], {x, 0, 2 Pi},
 GridLines -> {{4}, {}}]

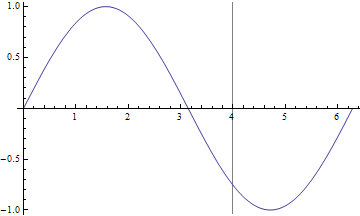
pour le cas de lignes horizontales en utilisant Plot le truc le plus simple est d'inclure des fonctions constantes supplémentaires:

Plot[{Sin[x], .75}, {x, 0, 2Pi}]

Pour les lignes verticales, il y a le Epilog option pour Plot et ListPlot:

Plot[Sin[x], {x, 0, 2Pi}, Epilog->Line[{{4,-100}, {4,100}}]]

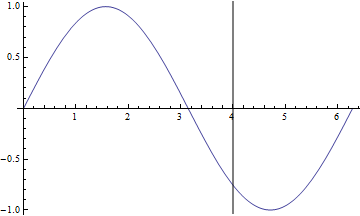
mais probablement le meilleur est le GridLines option donnée dans la réponse de Pillsy.

une approche serait d'ajouter Line primitives graphiques à vos graphismes:

p1 = Plot[Sin[x], {x, -2*Pi,2*Pi}];
l1 = Graphics@Line[{{-2Pi,.75},{2Pi,.75}}]; (* horizontal line at y==.75 *)
Show[p1,l1]

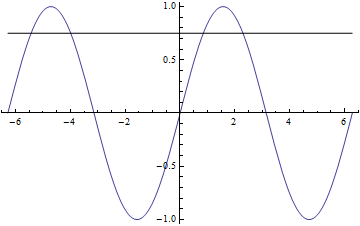
une Autre approche serait de jouer avec GridLines.

utilisez la commande Gridlines comme suit:

Plot[
  1/(15*E^((x - 100)^2/450)*Sqrt[2*Pi]),
  {x, 55, 145},
  GridLines -> {{85, 115}, {}}
]

traduction Dans le code ci-dessus, je trace une courbe normale:

1/(15*E^((x - 100)^2/450)*Sqrt[2*Pi]) 

alors dites à la parcelle quelle partie de l'axe des x je veux qu'elle affiche:

{x, 55, 145}

puis j'Ajoute les lignes verticales où je les veux à 85 et 115.

GridLines -> {{85, 115}, {}}

Remarque: vous devez fournir le vide {}Gridlines attendez lignes de la grille horizontale endroits.

une alternative est de penser la ligne verticale comme une ligne droite de pente infinie. Donc, pour une ligne verticale à situé à x=2*pi, on peut faire quelque chose comme ceci:

Plot[{Sin[x], 10^10 (x - 2 \[Pi])}, {x, 0, 10}, PlotRange -> {-1, 1}]

cliquez pour voir l'image

notez que le terme 10^10 imite une pente infinie. Si vous n'utilisez pas L'option PlotRange -> {-1, 1}, la fonction "dominante" est la ligne droite de sorte que la fonction Sin[x] apparaît effectivement comme une ligne horizontale.