Tracer une fonction complexe dans Mathematica
Comment puis-je faire un graphisme Mathematica qui copie le comportement de complex_plot dans sage? c'est à dire
... prend une fonction complexe d'une variable, et la production de placettes de la fonction sur le xrange spécifié et yrange comme démontré ci-dessous. Le l'ampleur de la sortie est indiqué par la luminosité (avec zéro étant noir et infini étant blanc) alors que l'argument est représenté par la teinte (avec rouge étant positif réel, et croissant en orange, jaune,... l'argument augmente).
voici un exemple (volé à M. Hampton de Drifts neutres ) de la fonction zeta avec des contours superposés de valeur absolue:
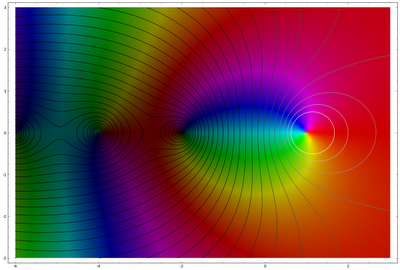
dans la page de documentation de Mathematica fonctions de Variables complexes il dit que vous pouvez visualisez les fonctions complexes en utilisant ContourPlot et DensityPlot "coloration potentielle par phase". Mais le problème est dans les deux types de tracés, ColorFunction ne prend qu'une seule variable égale au contour ou à la densité au point - il semble donc impossible de lui faire colorer la phase/argument tout en traçant la valeur absolue. Notez que ce n'est pas un problème avec Plot3D où tous les 3 paramètres (x,y,z) passent à ColorFunction .
je sais qu'il y a d'autres façons de visualiser des fonctions complexes - comme "l'exemple soigné" dans le Plot3D docs , mais ce n'est pas ce que je veux.
aussi, j'ai une solution en dessous de (qui a été effectivement utilisé pour générer certains graphiques utilisés dans Wikipedia), mais il définit une fonction de niveau assez bas, et je pense que cela devrait être possible avec une fonction de haut niveau comme ContourPlot ou DensityPlot . Non pas que cela devrait vous arrêter de donner votre approche préférée qui utilise une construction de niveau inférieur!
Edit: il y avait quelques beaux articles de Michael Trott dans le Mathematica journal sur:
Visualisation des surfaces de Riemann de fonctions algébriques , IIa , IIb , IIc , IId .
La visualisation de surfaces de Riemann démo .
Le Retour de surfaces de Riemann (mises à jour pour Mma v6)
bien sûr, Michael Trott a écrit le Mathematica guide books , qui contiennent de nombreux beaux graphiques, mais semblent avoir pris du retard sur le calendrier de publication accélérée Mathematica!
3 réponses
voici ma tentative. Je ailé de la fonction de mise en couleur un peu.
ParametricPlot[
(*just need a vis function that will allow x and y to be in the color function*)
{x, y}, {x, -6, 3}, {y, -3, 3},
(*color and mesh functions don't trigger refinement, so just use a big grid*)
PlotPoints -> 50, MaxRecursion -> 0, Mesh -> 50,
(*turn off scaling so we can do computations with the actual complex values*)
ColorFunctionScaling -> False,
ColorFunction -> (Hue[
(*hue according to argument, with shift so arg(z)==0 is red*)
Rescale[Arg[Zeta[# + I #2]], {-Pi, Pi}, {0, 1} + 0.5], 1,
(*fudge brightness a bit:
0.1 keeps things from getting too dark,
2 forces some actual bright areas*)
Rescale[Log[Abs[Zeta[# + I #2]]], {-Infinity, Infinity}, {0.1, 2}]] &),
(*mesh lines according to magnitude, scaled to avoid the pole at z=1*)
MeshFunctions -> {Log[Abs[Zeta[#1 + I #2]]] &},
(*turn off axes, because I don't like them with frames*)
Axes -> False
]
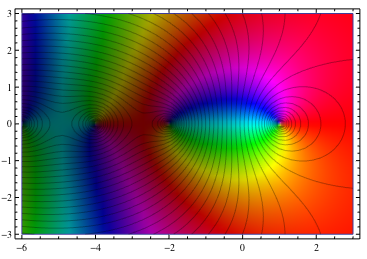
Je n'ai pas pensé à un bon moyen d'obtenir les lignes de maille pour varier dans la couleur. Le plus simple est probablement de simplement les générer avec ContourPlot au lieu de MeshFunctions .
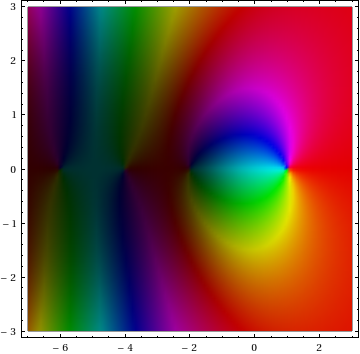
voici ma variation sur la fonction donnée par Axel Boldt qui a été inspiré par Jan Homann . Les deux pages liées ont de beaux graphismes.
ComplexGraph[f_, {xmin_, xmax_}, {ymin_, ymax_}, opts:OptionsPattern[]] :=
RegionPlot[True, {x, xmin, xmax}, {y, ymin, ymax}, opts,
PlotPoints -> 100, ColorFunctionScaling -> False,
ColorFunction -> Function[{x, y}, With[{ff = f[x + I y]},
Hue[(2. Pi)^-1 Mod[Arg[ff], 2 Pi], 1, 1 - (1.2 + 10 Log[Abs[ff] + 1])^-1]]]
]
alors nous pouvons faire le tracé sans les contours en exécutant
ComplexGraph[Zeta, {-7, 3}, {-3, 3}]
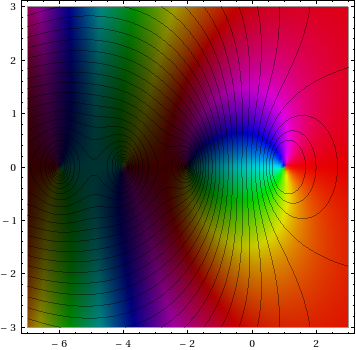
nous pouvons ajouter des contours en copiant Brett en utilisant et en montrant un maillage spécifique de la placette dans le graphe complexe:
ComplexGraph[Zeta, {-7, 3}, {-3, 3}, Mesh -> 30,
MeshFunctions -> {Log[Abs[Zeta[#1 + I #2]]] &},
MeshStyle -> {{Thin, Black}, None}, MaxRecursion -> 0]
ou en combinant avec un tracé de contour comme
ContourPlot[Abs[Zeta[x + I y]], {x, -7, 3}, {y, -3, 3}, PlotPoints -> 100,
Contours -> Exp@Range[-7, 1, .25], ContourShading -> None];
Show[{ComplexGraph[Zeta, {-7, 3}, {-3, 3}],%}]
réponse inappropriée, pour deux raisons:
- ce n'est pas ce que vous avez demandé""
- j'utilise sans vergogne le code de Brett
de toute façon, pour moi, ce qui suit est beaucoup plus clair à interpréter (la luminosité est ... Eh bien, juste la luminosité):
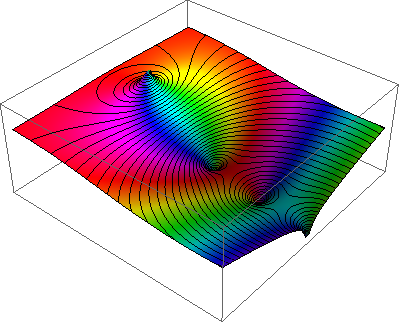
code de Brett presque intact:
Plot3D[
Log[Abs[Zeta[x + I y]]], {x, -6, 3}, {y, -3, 3},
(*color and mesh functions don't trigger refinement,so just use a big grid*)
PlotPoints -> 50, MaxRecursion -> 0,
Mesh -> 50,
(*turn off scaling so we can do computations with the actual complex values*)
ColorFunctionScaling -> False,
ColorFunction -> (Hue[
(*hue according to argument,with shift so arg(z)==0 is red*)
Rescale[Arg[Zeta[# + I #2]], {-Pi, Pi}, {0, 1} + 0.5],
1,(*fudge brightness a bit:
0.1 keeps things from getting too dark,
2 forces some actual bright areas*)
Rescale[Log[Abs[Zeta[# + I #2]]], {-Infinity, Infinity}, {0.1, 2}]] &),
(*mesh lines according to magnitude,scaled to avoid the pole at z=1*)
MeshFunctions -> {Log[Abs[Zeta[#1 + I #2]]] &},
(*turn off axes,because I don't like them with frames*)
Axes -> False]