Graphique des coordonnées parallèles dans Matplotlib
les données bidimensionnelles et tridimensionnelles peuvent être visualisées de façon relativement directe en utilisant les types de placettes traditionnels. Même avec quatre dimensions données, nous pouvons souvent trouver un moyen pour afficher les données. Les Dimensions au-dessus de quatre, cependant, deviennent de plus en plus difficiles à afficher. Heureusement, parallèle coordonnées parcelles fournir un mécanisme pour l'affichage des résultats avec les dimensions supérieures.
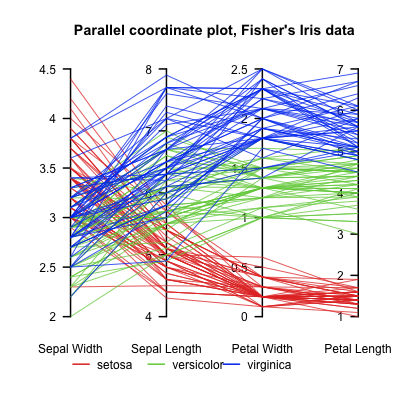
plusieurs les tracés fournissent des tracés de coordonnées parallèles, comme Matlab , R , VTK type 1 et VTK type 2 , mais je ne vois pas comment en créer un en utilisant Matplotlib.
- y a-t-il un tracé intégré de coordonnées parallèles dans Matplotlib? Je ne vois certainement pas un dans la galerie .
- s'il n'y a pas de type incorporé, est il est possible de construire un tracé de coordonnées parallèle en utilisant les caractéristiques standard de Matplotlib?
modifier :
basé sur la réponse fournie par Zhenya ci-dessous, j'ai développé la généralisation suivante qui supporte un nombre arbitraire d'axes. En suivant le style de l'exemple que j'ai posté dans la question originale ci-dessus, chaque axe obtient sa propre échelle. J'ai accompli ceci en normalisant les données à chaque point d'axe et rendre les axes ont une gamme de 0 à 1. Je reviens ensuite en arrière et applique des étiquettes à chaque marque de tique qui donnent la valeur correcte à cette interception.
la fonction fonctionne en acceptant un itérable d'ensembles de données. Chaque ensemble de données est considéré comme un ensemble de points où chaque point se situe sur un axe différent. L'exemple dans __main__ saisit des nombres aléatoires pour chaque axe en deux ensembles de 30 lignes. Les lignes sont aléatoires à l'intérieur des fourchettes qui causent le regroupement des lignes; un comportement que je voulais vérifier.
Cette solution n'est pas aussi bonne qu'une solution intégrée car vous avez un comportement de souris étrange et je simule les plages de données à travers les étiquettes, mais Jusqu'à ce que Matplotlib ajoute une solution intégrée, c'est acceptable.
#!/usr/bin/python
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
def parallel_coordinates(data_sets, style=None):
dims = len(data_sets[0])
x = range(dims)
fig, axes = plt.subplots(1, dims-1, sharey=False)
if style is None:
style = ['r-']*len(data_sets)
# Calculate the limits on the data
min_max_range = list()
for m in zip(*data_sets):
mn = min(m)
mx = max(m)
if mn == mx:
mn -= 0.5
mx = mn + 1.
r = float(mx - mn)
min_max_range.append((mn, mx, r))
# Normalize the data sets
norm_data_sets = list()
for ds in data_sets:
nds = [(value - min_max_range[dimension][0]) /
min_max_range[dimension][2]
for dimension,value in enumerate(ds)]
norm_data_sets.append(nds)
data_sets = norm_data_sets
# Plot the datasets on all the subplots
for i, ax in enumerate(axes):
for dsi, d in enumerate(data_sets):
ax.plot(x, d, style[dsi])
ax.set_xlim([x[i], x[i+1]])
# Set the x axis ticks
for dimension, (axx,xx) in enumerate(zip(axes, x[:-1])):
axx.xaxis.set_major_locator(ticker.FixedLocator([xx]))
ticks = len(axx.get_yticklabels())
labels = list()
step = min_max_range[dimension][2] / (ticks - 1)
mn = min_max_range[dimension][0]
for i in xrange(ticks):
v = mn + i*step
labels.append('%4.2f' % v)
axx.set_yticklabels(labels)
# Move the final axis' ticks to the right-hand side
axx = plt.twinx(axes[-1])
dimension += 1
axx.xaxis.set_major_locator(ticker.FixedLocator([x[-2], x[-1]]))
ticks = len(axx.get_yticklabels())
step = min_max_range[dimension][2] / (ticks - 1)
mn = min_max_range[dimension][0]
labels = ['%4.2f' % (mn + i*step) for i in xrange(ticks)]
axx.set_yticklabels(labels)
# Stack the subplots
plt.subplots_adjust(wspace=0)
return plt
if __name__ == '__main__':
import random
base = [0, 0, 5, 5, 0]
scale = [1.5, 2., 1.0, 2., 2.]
data = [[base[x] + random.uniform(0., 1.)*scale[x]
for x in xrange(5)] for y in xrange(30)]
colors = ['r'] * 30
base = [3, 6, 0, 1, 3]
scale = [1.5, 2., 2.5, 2., 2.]
data.extend([[base[x] + random.uniform(0., 1.)*scale[x]
for x in xrange(5)] for y in xrange(30)])
colors.extend(['b'] * 30)
parallel_coordinates(data, style=colors).show()
Edit 2:
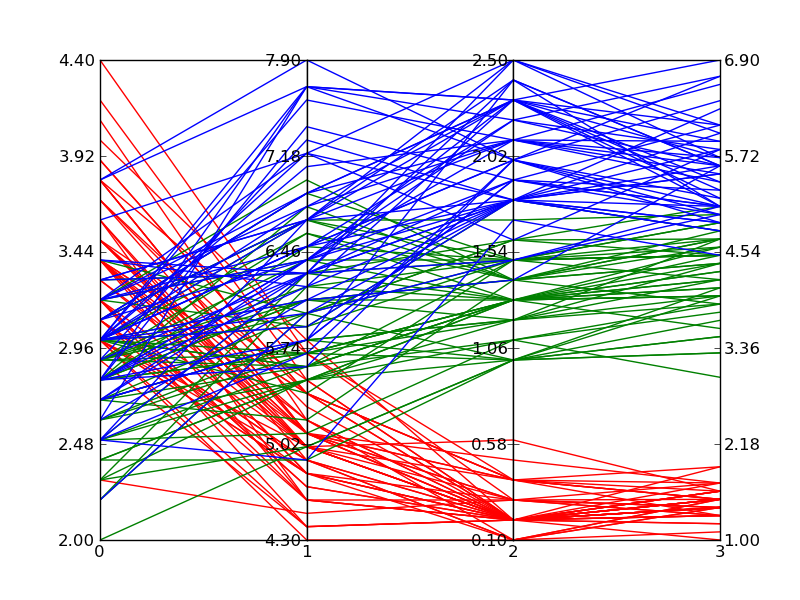
voici un exemple de ce qui ressort du code ci-dessus en traçant Fisher'S Iris data . Il n'est pas assez aussi agréable que L'image de référence de Wikipedia, mais il est acceptable si tout ce que vous avez Est Matplotlib et vous avez besoin de tracés multidimensionnels.
4 réponses
je suis sûr qu'il y a une meilleure façon de le faire, mais en voici une rapide et sale (une vraiment sale):
#!/usr/bin/python
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
#vectors to plot: 4D for this example
y1=[1,2.3,8.0,2.5]
y2=[1.5,1.7,2.2,2.9]
x=[1,2,3,8] # spines
fig,(ax,ax2,ax3) = plt.subplots(1, 3, sharey=False)
# plot the same on all the subplots
ax.plot(x,y1,'r-', x,y2,'b-')
ax2.plot(x,y1,'r-', x,y2,'b-')
ax3.plot(x,y1,'r-', x,y2,'b-')
# now zoom in each of the subplots
ax.set_xlim([ x[0],x[1]])
ax2.set_xlim([ x[1],x[2]])
ax3.set_xlim([ x[2],x[3]])
# set the x axis ticks
for axx,xx in zip([ax,ax2,ax3],x[:-1]):
axx.xaxis.set_major_locator(ticker.FixedLocator([xx]))
ax3.xaxis.set_major_locator(ticker.FixedLocator([x[-2],x[-1]])) # the last one
# EDIT: add the labels to the rightmost spine
for tick in ax3.yaxis.get_major_ticks():
tick.label2On=True
# stack the subplots together
plt.subplots_adjust(wspace=0)
plt.show()
C'est essentiellement basée sur une (beaucoup plus sympa) un par Joe Kingon, Python/Matplotlib existe - il un moyen de faire un discontinu de l'axe? . Vous pourriez aussi vouloir jeter un oeil à l'autre réponse à la même question.
dans cet exemple, je n'essaie même pas de mettre à l'échelle les échelles verticales, car il dépend exactement ce que vous essayez d'atteindre.
EDIT: voici le résultat 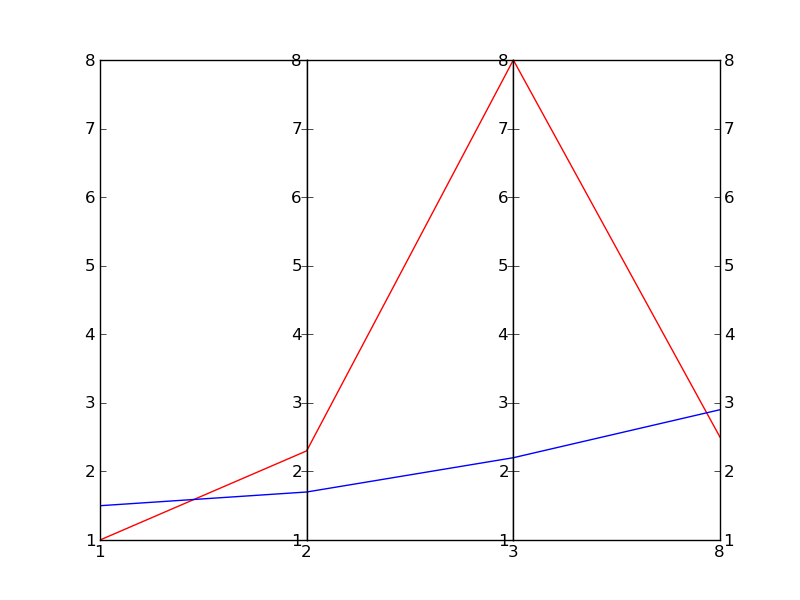
pandas a une enveloppe de coordonnées parallèles:
import pandas
import matplotlib.pyplot as plt
from pandas.tools.plotting import parallel_coordinates
data = pandas.read_csv(r'C:\Python27\Lib\site-packages\pandas\tests\data\iris.csv', sep=',')
parallel_coordinates(data, 'Name')
plt.show()
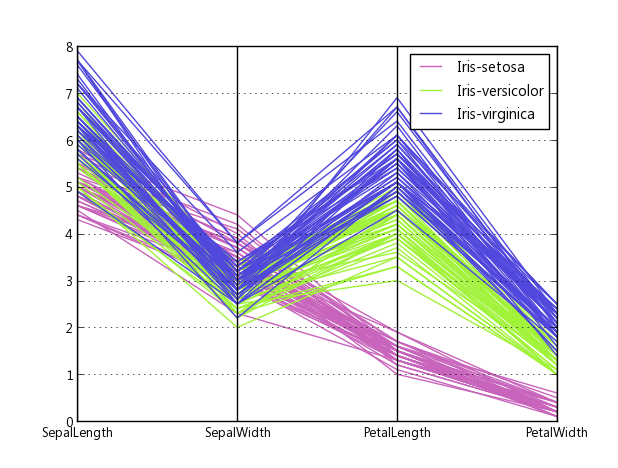
code Source, comment ils l'ont fait: traçage.py#L494
s'il vous plaît noter: Lors de l'utilisation de pandas (comme suggéré par theta), il n'y a aucun moyen de dimensionner les axes indépendamment.
la raison pour laquelle vous ne pouvez pas trouver les différents axes verticaux est qu'il n'y en a pas. Nos coordonnées parallèles "simulent" les deux autres axes en dessinant simplement une ligne verticale et quelques étiquettes.
https://github.com/pydata/pandas/issues/7083#issuecomment-74253671
Désolé, je ne peux pas l'ajouter comme un commentaire direct (réputation <50)
le meilleur exemple que j'ai vu jusqu'à présent est celui-ci
https://python.g-node.org/python-summerschool-2013/_media/wiki/datavis/olympics_vis.py
voir la fonction normalised_coordinates. Pas super rapide, mais ça fonctionne à partir de ce que j'ai essayé.
normalised_coordinates(['VAL_1', 'VAL_2', 'VAL_3'], np.array([[1230.23, 1500000, 12453.03], [930.23, 140000, 12453.03], [130.23, 120000, 1243.03]]), [1, 2, 1])