OpenCV triangulatePoints handedness

j'ai deux caméras attachées rigidement côte à côte, regardant en parallèle.

matrice de Projection pour gauche de la caméra

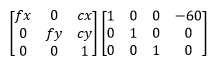
matrice de Projection pour droit de la caméra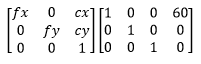

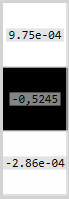
quand j'exécute triangulatePoints sur les deux vecteurs des points correspondants, J'obtiens la collection de points dans L'espace 3D. Tous les points de L'espace 3D ont une coordonnée Z négative .

Donc, pour aller au fond de cette...

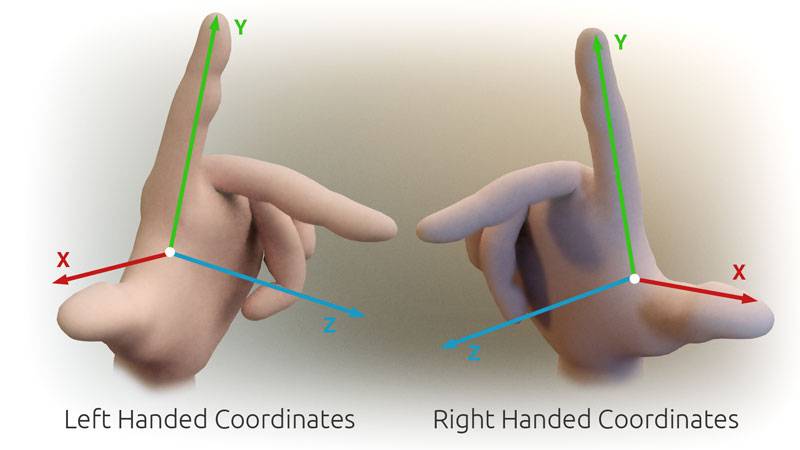
mon hypothèse était Qu'OpenCV utilise un système de coordonnées de droite.

le rappel de la main:

je suppose que l'orientation initiale de chaque caméra dans la direction positive de l'axe Z .

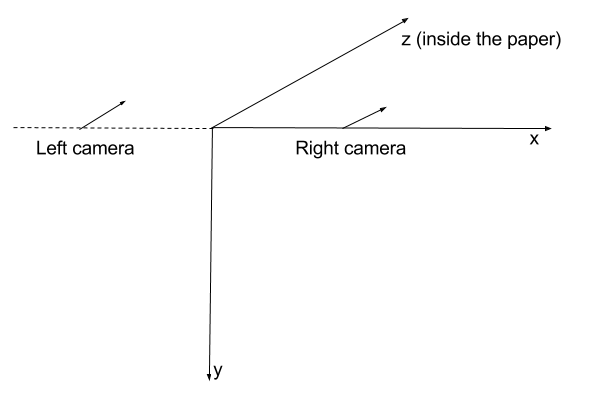
donc, en utilisant les matrices de projection comme celles que j'ai présentées au début, je suppose que les caméras sont positionnées dans l'espace comme ceci:

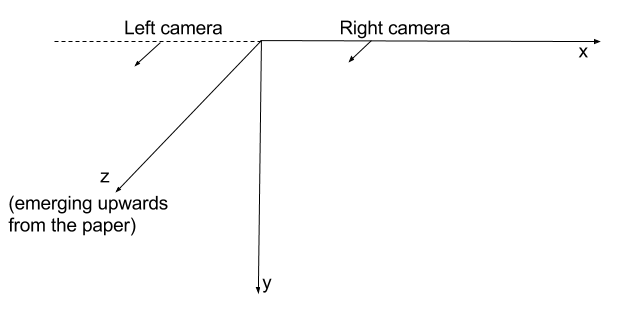
cette hypothèse est en contradiction avec ce que j'observe lorsque je reçois des corrdinates z négatifs pour les points tracés. La seule explication que je peux pensez à OpenCV qui utilise en fait le système de coordonnées de gauche. Ainsi, avec les matrices de projection que j'ai indiquées au début, c'est ainsi que les caméras sont positionnées dans l'espace:

cela indiquerait que ma caméra gauche dans cette situation n'est pas du côté gauche . Et c'est pourquoi j'obtiens une profondeur négative pour les points.

Par ailleurs, si j'essaie de combiner triangulatePoints avec solvePnP je rencontre des problèmes.

j'utilise la sortie de triangulatePoints comme entrée à solvePnP . Je m'attends à obtenir les coordonnées de la caméra près de l'origine du système de coordonnées 3D. Je m'attends à ce que la position calculée de la caméra corresponde aux matrices de projection utilisées au début. Mais ce n'est pas le cas. J'obtiens des résultats complètement sauvages, manquant les valeurs attendues de plus de 10 fois la longueur de base.

exemple

cet exemple est une représentation plus complète du problème que ce qui est indiqué ci-dessus.

points3D

ici est le code pour générer ces points.

aller de l'avant, réglage de la caméra de Un et caméra D ...

Mat cameraMatrix = (Mat_<double>(3, 3) <<
    716.731, 0, 660.749,
    0, 716.731, 360.754,
    0, 0, 1);
Mat distCoeffs = (Mat_<double>(5, 1) << 0, 0, 0, 0, 0);



Mat rotation_a = Mat::eye(3, 3, CV_64F); // no rotation
Mat translation_a = (Mat_<double>(3, 1) << 0, 0, 0); // no translation
Mat rt_a;
hconcat(rotation_a, translation_a, rt_a);
Mat projectionMatrix_a = cameraMatrix * rt_a; 

Mat rotation_d = (Mat_<double>(3, 1) << 0, CV_PI / 6.0, 0); // 30° rotation about Y axis
Rodrigues(rotation_d, rotation_d); // convert to 3x3 matrix
Mat translation_d = (Mat_<double>(3, 1) << 100, 0, 0);
Mat rt_d;
hconcat(rotation_d, translation_d, rt_d);
Mat projectionMatrix_d = cameraMatrix * rt_d;

quelles sont les coordonnées pixel de points3D lorsqu'elles sont observées par les projections A et d .

Mat points2D_a = projectionMatrix_a * points3D;
Mat points2D_d = projectionMatrix_d * points3D;

je les mets dans des vecteurs:

vector<Point2f> points2Dvector_a, points2Dvector_d;

après cela, je génère à nouveau les points 3D.

Mat points3DHomogeneous;
triangulatePoints(projectionMatrix_a, projectionMatrix_d, points2Dvector_a, points2Dvector_d, points3DHomogeneous);
Mat triangulatedPoints3D;
transpose(points3DHomogeneous, triangulatedPoints3D);
convertPointsFromHomogeneous(triangulatedPoints3D, triangulatedPoints3D);

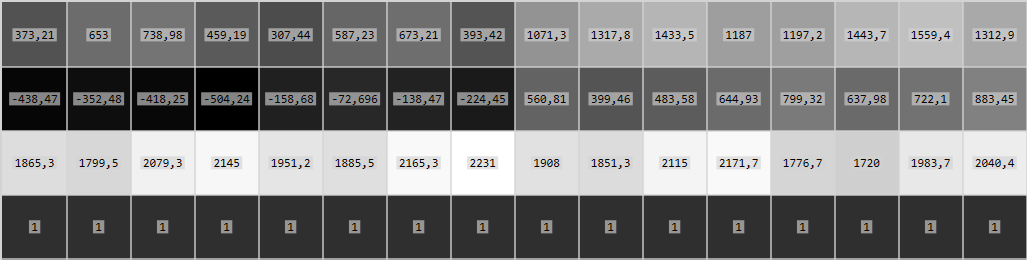
Maintenant, triangulatedPoints3D démarrer comme ceci:

et ils sont identiques à points3D .

Et puis la dernière étape.

Mat rvec, tvec;
solvePnP(triangulatedPoints3D, points2Dvector_d, cameraMatrix, distCoeffs, rvec, tvec);

Résultant rvec et tvec :

j'avais espéré obtenir quelque chose de plus similaire aux transformations utilisées dans la création de projectionMatrix_d , i.e. traduction de (100, 0, 0) et la rotation de 30° sur l'axe y.

si j'utilise des transformations inversées lors de la création de matrices de projection, comme ceci:

Mat rotation_d = (Mat_<double>(3, 1) << 0, CV_PI / 6.0, 0); // 30° rotation about Y axis
Rodrigues(-rotation_d, rotation_d); // NEGATIVE ROTATION
Mat translation_d = (Mat_<double>(3, 1) << 100, 0, 0);
Mat rt_d;
hconcat(rotation_d, -translation_d, rt_d); // NEGATIVE TRANSLATION
Mat projectionMatrix_d = cameraMatrix * rt_d;

puis je reçois rvec et tvec :

et c'est beaucoup plus logique. Mais ensuite je change le début transformation de sorte que la rotation est négative CV_PI / 6.0 - > -CV_PI / 6.0 et le résultat rvec et tvec sont:

je voudrais trouver une explication de ce qui se passe. Pourquoi j'obtiens des résultats bizarres de solvePnP .