O (N log N) complexité-semblable à linéaire?
donc je pense que je vais me faire enterrer pour avoir posé une question aussi insignifiante mais je suis un peu confus à propos de quelque chose.
j'ai implémenté quicksort en Java et C et je faisais quelques comparaisons de base. Le graphe est sorti comme deux lignes droites, avec le C étant 4MS plus rapide que la contrepartie Java plus de 100.000 entiers aléatoires.
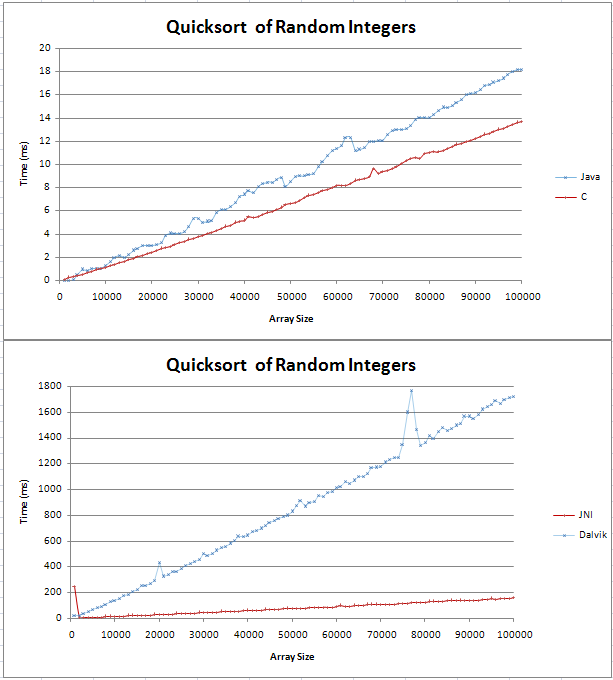
le code de mes tests se trouve ici;
android-repères
Je ne savais pas à quoi ressemblerait une ligne (n log n), mais je ne pensais pas qu'elle serait droite. Je voulais juste vérifier que c'est le résultat attendu et que je ne devrais pas essayer de trouver une erreur dans mon code.
j'ai collé la formule dans excel et pour la base 10 il semble être une ligne droite avec un kink au départ. Est-ce parce que la différence entre log(n) log(n+1) augmente linéairement?
Merci,
Gav
7 réponses
faites le graphe plus grand et vous verrez que o (logn) n'est pas tout à fait une ligne droite. Mais oui, c'est assez proche du comportement linéaire. Pour voir pourquoi, il suffit de prendre le logarithme de quelques très grands nombres.
par exemple (base 10):
log(1000000) = 6
log(1000000000) = 9
…
ainsi, pour trier 1.000.000 de nombres, un tri O(N logn) ajoute un facteur de mesure 6 (ou juste un peu plus puisque la plupart des algorithmes de tri dépendra des logarithmes de base 2). Pas mal de choses à.
en fait, ce facteur logarithmique est so extraordinairement petit que pour la plupart des ordres de grandeur, les algorithmes O(N logn) établis dépassent les algorithmes linéaires de temps. Un exemple important est la création d'une structure de données de tableau de suffixe.
un cas simple m'a récemment mordu quand j'ai essayé d'améliorer un tri rapide de cordes courtes en employant le tri radix . Il s'avère, pour de courtes cordes, que ce (temps linéaire) radix le tri était plus rapide que le quicksort, mais il y avait un point de bascule pour les cordes encore relativement courtes, puisque le tri radix dépend de façon cruciale de la longueur des cordes que vous triez.
pour information, quicksort est en fait O (N^2), mais avec un cas moyen de O (nlogn)
POUR INFO, il y a une grande différence entre O(n) et O(nlogn). C'est pourquoi il n'est pas lié par O(n) pour aucune constante.
pour une démonstration graphique, Voir:
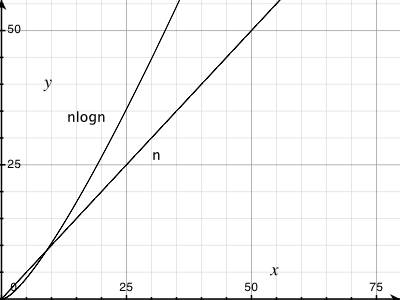
pour encore plus de plaisir dans une veine similaire, essayez de tracer le temps pris par n opérations sur la norme disjoint set data structure . Il a été démontré qu'il est asymptotiquement n α( n ) Où α ( n ) est l'inverse de la fonction Ackermann (bien que vos algorithmes habituels manuel ne montrera probablement une limite de n journal le journal de n ou éventuellement n journal* n ). Pour tout type de nombre que vous serez susceptible de rencontrer comme la taille d'entrée, α( n ) ≤ 5 (et en effet log* n ≤ 5), bien qu'il approche l'infini asymptotiquement.
ce que je suppose que vous pouvez apprendre de ceci est que tandis que la complexité asymptotique est un outil très utile pour penser algorithmes, ce n'est pas tout à fait la même chose que l'efficacité pratique.
- habituellement, les algorithmes O( N*log(n) ) ont une implémentation logarithmique à 2 bases.
- Pour n = 1024, log(1024) = 10, alors n*log(n) = 1024*10 = 10240 calculs, une augmentation d'un ordre de grandeur.
Alors, O(n*log(n)) est similaire aux linéaire que pour une petite quantité de données.
astuce: n'oubliez pas que quicksort se comporte très bien sur les données aléatoires et que ce n'est pas un algorithme O(N*log(n)).
toutes les données peuvent être tracées sur une ligne si les axes sont choisis correctement: -)
Wikipedia dit que Big-O est le pire des cas (i.e. f (x) est O(N) signifie que f(x) est "borné au-dessus" par N) https://en.wikipedia.org/wiki/Big_O_notation
Voici une belle série de graphiques illustrant les différences entre les diverses fonctions communes: http://science.slc.edu/~jmarshall/cours/2002/printemps/cs50/BigO/
la dérivée du log(x) est de 1/x. C'est la vitesse à laquelle log(x) augmente à mesure que x augmente. Il n'est pas linéaire, bien qu'il puisse ressembler à une ligne droite parce qu'il se plie si lentement. Quand je pense à O (log(n)), je pense à O(N^0+), c'est-à-dire à la plus petite puissance de N qui n'est pas une constante, car toute puissance constante positive de N finira par la dépasser. Ce n'est pas exact à 100%, donc les professeurs vont s'énerver contre toi si tu l'expliques de cette façon.
la différence entre les logs de deux bases différentes est un multiplicateur constant. Rechercher la formule pour convertir les logs entre deux bases: (sous" changement de base "ici: https://en.wikipedia.org/wiki/Logarithm ) L'astuce est de traiter k et b comme des constantes.
dans la pratique, il y aura normalement quelques hoquets dans toutes les données que vous tracez. Il y aura des différences dans les choses en dehors de votre programme (quelque chose qui change dans le cpu avant votre programme, les erreurs de cache, etc.). Il prend de nombreuses pistes d'obtenir des données fiables. Les constantes sont le plus grand ennemi d'essayer d'appliquer la notation Big O à l'exécution réelle. Un algorithme O(N) avec une constante élevée peut être plus lent qu'un algorithme O(N^2) pour un nombre suffisamment petit de N.
log(N) est (très) peu près le nombre de chiffres de N. Donc, pour la plupart, il y a peu de différence entre log(n) log(n+1)
essayez de tracer une ligne linéaire réelle sur le dessus de celui-ci et vous verrez la petite augmentation. Notez que la valeur de Y à 50 000 est inférieure à la valeur de 1/2 Y à 100 000.
C'est là, mais c'est petit. C'est pourquoi O(nlog(n)) est si bon!