Num PY: produit cartésien des points des tableaux x et y en un seul tableau de points 2D

a canonique cartesian_product (presque)

Il existe de nombreuses approches à ce problème avec des propriétés différentes. Certains sont plus rapides que d'autres, et certains sont plus d'usage général. Après beaucoup de tests et de retouches, j'ai trouvé que la fonction suivante, qui calcule un n-dimensionnel cartesian_product , est plus rapide que la plupart des autres pour de nombreuses entrées. Pour une paire d'approches qui sont un peu plus complexes, mais sont même un peu plus rapides dans de nombreux cas, voir la réponse par Paul Panzer .

étant donné cette réponse, ce n'est plus la plus rapide mise en œuvre du produit cartésien dans numpy que je connais. Cependant, je pense que sa simplicité continuera d'en faire un point de référence utile pour l'amélioration future:

def cartesian_product(*arrays):
    la = len(arrays)
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty([len(a) for a in arrays] + [la], dtype=dtype)
    for i, a in enumerate(numpy.ix_(*arrays)):
        arr[...,i] = a
    return arr.reshape(-1, la)

Il est important de mentionner que cette fonction utilise ix_ d'une manière inhabituelle; considérant que l'utilisation documentée de ix_ est pour générer des indices dans un tableau, il se trouve que des tableaux avec la même forme peuvent être utilisés pour l'assignation diffusée. Un grand merci à mgilson , qui m'a inspiré à essayer d'utiliser ix_ de cette façon, et à unutbu , qui a fourni quelques commentaires extrêmement utiles sur cette réponse, y compris la suggestion d'utiliser numpy.result_type .

Solutions de rechange notables

il est parfois plus rapide d'écrire des blocs contigus de mémoire dans L'ordre Fortran. C'est la base de cette alternative, cartesian_product_transpose , qui s'est avérée plus rapide sur certains matériels que cartesian_product (voir ci-dessous). Cependant, la réponse de Paul Panzer, qui utilise le même principe, est encore plus rapide. Pourtant, je l'inclus ici pour les lecteurs intéressés:

def cartesian_product_transpose(*arrays):
    broadcastable = numpy.ix_(*arrays)
    broadcasted = numpy.broadcast_arrays(*broadcastable)
    rows, cols = numpy.prod(broadcasted[0].shape), len(broadcasted)
    dtype = numpy.result_type(*arrays)

    out = numpy.empty(rows * cols, dtype=dtype)
    start, end = 0, rows
    for a in broadcasted:
        out[start:end] = a.reshape(-1)
        start, end = end, end + rows
    return out.reshape(cols, rows).T

après être venu pour comprendre L'approche de Panzer, j'ai écrit une nouvelle version c'est presque aussi rapide que le sien, et est presque aussi simple que cartesian_product :

def cartesian_product_simple_transpose(arrays):
    la = len(arrays)
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty([la] + [len(a) for a in arrays], dtype=dtype)
    for i, a in enumerate(numpy.ix_(*arrays)):
        arr[i, ...] = a
    return arr.reshape(la, -1).T

cela semble avoir un certain temps constant qui le rend courir plus lent que Panzer pour de petites entrées. Mais pour des entrées plus importantes, dans tous les tests que j'ai effectués, il fonctionne aussi bien que son implémentation la plus rapide ( cartesian_product_transpose_pp ).

dans les sections suivantes, j'inclus quelques tests d'autres alternatives. Ils sont maintenant un peu dépassés, mais plutôt que double effort, j'ai décidé de les laisser ici par intérêt historique. Pour des tests actualisés, voir la réponse de Panzer, ainsi que Nico Schlömer 's.

les Tests de comparaison des alternatives

Voici une batterie de tests qui montrent l'augmentation de performance que certaines de ces fonctions fournissent par rapport à un certain nombre d'alternatives. Tous les tests présentés ici ont été effectués sur une machine quad-core, faisant tourner Mac OS 10.12.5, Python 3.6.1, et numpy 1.12.1. Les Variations sur le matériel et le logiciel sont connus pour produire des résultats différents, donc YMMV. Exécutez ces tests pour vous-même pour être sûr!

Définitions:

import numpy
import itertools
from functools import reduce

### Two-dimensional products ###

def repeat_product(x, y):
    return numpy.transpose([numpy.tile(x, len(y)), 
                            numpy.repeat(y, len(x))])

def dstack_product(x, y):
    return numpy.dstack(numpy.meshgrid(x, y)).reshape(-1, 2)

### Generalized N-dimensional products ###

def cartesian_product(*arrays):
    la = len(arrays)
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty([len(a) for a in arrays] + [la], dtype=dtype)
    for i, a in enumerate(numpy.ix_(*arrays)):
        arr[...,i] = a
    return arr.reshape(-1, la)

def cartesian_product_transpose(*arrays):
    broadcastable = numpy.ix_(*arrays)
    broadcasted = numpy.broadcast_arrays(*broadcastable)
    rows, cols = numpy.prod(broadcasted[0].shape), len(broadcasted)
    dtype = numpy.result_type(*arrays)

    out = numpy.empty(rows * cols, dtype=dtype)
    start, end = 0, rows
    for a in broadcasted:
        out[start:end] = a.reshape(-1)
        start, end = end, end + rows
    return out.reshape(cols, rows).T

# from https://stackoverflow.com/a/1235363/577088

def cartesian_product_recursive(*arrays, out=None):
    arrays = [numpy.asarray(x) for x in arrays]
    dtype = arrays[0].dtype

    n = numpy.prod([x.size for x in arrays])
    if out is None:
        out = numpy.zeros([n, len(arrays)], dtype=dtype)

    m = n // arrays[0].size
    out[:,0] = numpy.repeat(arrays[0], m)
    if arrays[1:]:
        cartesian_product_recursive(arrays[1:], out=out[0:m,1:])
        for j in range(1, arrays[0].size):
            out[j*m:(j+1)*m,1:] = out[0:m,1:]
    return out

def cartesian_product_itertools(*arrays):
    return numpy.array(list(itertools.product(*arrays)))

### Test code ###

name_func = [('repeat_product',                                                 
              repeat_product),                                                  
             ('dstack_product',                                                 
              dstack_product),                                                  
             ('cartesian_product',                                              
              cartesian_product),                                               
             ('cartesian_product_transpose',                                    
              cartesian_product_transpose),                                     
             ('cartesian_product_recursive',                           
              cartesian_product_recursive),                            
             ('cartesian_product_itertools',                                    
              cartesian_product_itertools)]

def test(in_arrays, test_funcs):
    global func
    global arrays
    arrays = in_arrays
    for name, func in test_funcs:
        print('{}:'.format(name))
        %timeit func(*arrays)

def test_all(*in_arrays):
    test(in_arrays, name_func)

# `cartesian_product_recursive` throws an 
# unexpected error when used on more than
# two input arrays, so for now I've removed
# it from these tests.

def test_cartesian(*in_arrays):
    test(in_arrays, name_func[2:4] + name_func[-1:])

x10 = [numpy.arange(10)]
x50 = [numpy.arange(50)]
x100 = [numpy.arange(100)]
x500 = [numpy.arange(500)]
x1000 = [numpy.arange(1000)]

résultats des tests:

In [2]: test_all(*(x100 * 2))
repeat_product:
67.5 µs ± 633 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
dstack_product:
67.7 µs ± 1.09 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
cartesian_product:
33.4 µs ± 558 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
cartesian_product_transpose:
67.7 µs ± 932 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
cartesian_product_recursive:
215 µs ± 6.01 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
cartesian_product_itertools:
3.65 ms ± 38.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

In [3]: test_all(*(x500 * 2))
repeat_product:
1.31 ms ± 9.28 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
dstack_product:
1.27 ms ± 7.5 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
cartesian_product:
375 µs ± 4.5 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
cartesian_product_transpose:
488 µs ± 8.88 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
cartesian_product_recursive:
2.21 ms ± 38.4 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_itertools:
105 ms ± 1.17 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [4]: test_all(*(x1000 * 2))
repeat_product:
10.2 ms ± 132 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
dstack_product:
12 ms ± 120 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product:
4.75 ms ± 57.1 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_transpose:
7.76 ms ± 52.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_recursive:
13 ms ± 209 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_itertools:
422 ms ± 7.77 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

dans tous les cas, cartesian_product tel que défini au début de cette réponse est le plus rapide.

pour les fonctions qui acceptent un nombre arbitraire de tableaux d'entrées, il vaut la peine vérifier les performances quand len(arrays) > 2 aussi. (Jusqu'à ce que je puisse déterminer pourquoi cartesian_product_recursive jette une erreur dans ce cas, je l'ai retiré de ces tests.)

In [5]: test_cartesian(*(x100 * 3))
cartesian_product:
8.8 ms ± 138 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_transpose:
7.87 ms ± 91.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_itertools:
518 ms ± 5.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [6]: test_cartesian(*(x50 * 4))
cartesian_product:
169 ms ± 5.1 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
cartesian_product_transpose:
184 ms ± 4.32 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
cartesian_product_itertools:
3.69 s ± 73.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [7]: test_cartesian(*(x10 * 6))
cartesian_product:
26.5 ms ± 449 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
cartesian_product_transpose:
16 ms ± 133 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cartesian_product_itertools:
728 ms ± 16 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [8]: test_cartesian(*(x10 * 7))
cartesian_product:
650 ms ± 8.14 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
cartesian_product_transpose:
518 ms ± 7.09 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
cartesian_product_itertools:
8.13 s ± 122 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

comme le montrent ces tests, cartesian_product reste concurrentiel jusqu'à ce que le nombre de tableaux d'entrées dépasse (approximativement) quatre. Après cela, cartesian_product_transpose a un léger bord.

il est intéressant de rappeler que les utilisateurs avec d'Autres matériels et d'exploitation les systèmes peuvent donner des résultats différents. Par exemple, unutbu déclare avoir vu les résultats suivants pour ces tests en utilisant Ubuntu 14.04, Python 3.4.3, et numpy 1.14.0.dev0+b7050a9:

>>> %timeit cartesian_product_transpose(x500, y500) 
1000 loops, best of 3: 682 µs per loop
>>> %timeit cartesian_product(x500, y500)
1000 loops, best of 3: 1.55 ms per loop

ci-dessous, je vais entrer dans quelques détails sur les tests précédents que j'ai effectués dans ce sens. La performance relative de ces approches a changé avec le temps, pour différents matériels et différentes versions de Python et numpy . Alors il n'est pas immédiatement utile pour les personnes en utilisant des versions à jour de numpy , il illustre comment les choses ont changé depuis la première version de cette réponse.

une alternative simple: meshgrid + dstack

la réponse actuellement acceptée utilise tile et repeat pour diffuser deux tableaux ensemble. Mais la fonction meshgrid fait pratiquement la même chose. Voici la sortie de tile et repeat avant d'être passé à transposer:

In [1]: import numpy
In [2]: x = numpy.array([1,2,3])
   ...: y = numpy.array([4,5])
   ...: 

In [3]: [numpy.tile(x, len(y)), numpy.repeat(y, len(x))]
Out[3]: [array([1, 2, 3, 1, 2, 3]), array([4, 4, 4, 5, 5, 5])]

et voici la sortie de meshgrid :

In [4]: numpy.meshgrid(x, y)
Out[4]: 
[array([[1, 2, 3],
        [1, 2, 3]]), array([[4, 4, 4],
        [5, 5, 5]])]

comme vous pouvez le voir, c'est presque identique. Nous n'avons qu'à reformuler le résultat pour obtenir exactement le même résultat.

In [5]: xt, xr = numpy.meshgrid(x, y)
   ...: [xt.ravel(), xr.ravel()]
Out[5]: [array([1, 2, 3, 1, 2, 3]), array([4, 4, 4, 5, 5, 5])]

plutôt que de remodeler à ce point, cependant, nous pourrions passer la sortie de meshgrid à dstack et remodeler ensuite, ce qui sauve du travail:

In [6]: numpy.dstack(numpy.meshgrid(x, y)).reshape(-1, 2)
Out[6]: 
array([[1, 4],
       [2, 4],
       [3, 4],
       [1, 5],
       [2, 5],
       [3, 5]])

contrairement à la revendication dans ce commentaire , Je n'ai vu aucune évidence que des entrées différentes produiront des sorties de forme différente, et comme le montre ci-dessus, ils font des choses très similaires, il serait donc assez étrange s'ils le faisaient. Faites-moi savoir si vous trouvez un contre-exemple.

Testing meshgrid + dstack vs. repeat + transpose

la performance relative de ces deux approches a changé au fil du temps. Dans un version précédente de Python (2.7), le résultat en utilisant meshgrid + dstack était nettement plus rapide pour les petites entrées. (Veuillez noter que ces tests sont tirés d'une ancienne version de cette réponse.) Définitions:

>>> def repeat_product(x, y):
...     return numpy.transpose([numpy.tile(x, len(y)), 
                                numpy.repeat(y, len(x))])
...
>>> def dstack_product(x, y):
...     return numpy.dstack(numpy.meshgrid(x, y)).reshape(-1, 2)
...     

pour une entrée de taille moyenne, j'ai vu une accélération significative. Mais j'ai récupéré ces tests avec des versions plus récentes de Python (3.6.1) et numpy (1.12.1), sur une nouvelle machine. Les deux approches sont presque identiques maintenant.

Ancien Essai

>>> x, y = numpy.arange(500), numpy.arange(500)
>>> %timeit repeat_product(x, y)
10 loops, best of 3: 62 ms per loop
>>> %timeit dstack_product(x, y)
100 loops, best of 3: 12.2 ms per loop

Nouvel Essai

In [7]: x, y = numpy.arange(500), numpy.arange(500)
In [8]: %timeit repeat_product(x, y)
1.32 ms ± 24.7 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [9]: %timeit dstack_product(x, y)
1.26 ms ± 8.47 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

comme toujours, YMMV, mais cela suggère que dans les versions récentes de Python et de numpy, ceux-ci sont interchangeables.

fonctions de produits généralisées

En général, on pourrait s'attendre à ce que l'utilisation de fonctions intégrées sera plus rapide pour les petites entrées, tandis que pour les grandes entrées, un la fonction pourrait être plus rapide. De plus, pour un produit généralisé de dimension n, tile et repeat ne serviront à rien, car ils n'ont pas d'analogues clairs de dimension supérieure. Il vaut donc la peine d'étudier le comportement des fonctions spécialement conçues.

la plupart des tests pertinents apparaissent au début de cette réponse, mais voici quelques-uns des tests effectués sur les versions précédentes de Python et numpy pour comparaison.

le cartesian fonction définie dans une autre réponse utilisée pour effectuer assez bien pour des entrées plus grandes. (C'est la même chose que la fonction appelée cartesian_product_recursive ci-dessus.) Pour comparer cartesian à dstack_prodct , nous n'utilisons que deux dimensions.

Ici encore, l'ancien test a montré une différence significative, tandis que le nouveau test montre presque aucun.

Ancien Test

>>> x, y = numpy.arange(1000), numpy.arange(1000)
>>> %timeit cartesian([x, y])
10 loops, best of 3: 25.4 ms per loop
>>> %timeit dstack_product(x, y)
10 loops, best of 3: 66.6 ms per loop

Nouvel Essai

In [10]: x, y = numpy.arange(1000), numpy.arange(1000)
In [11]: %timeit cartesian([x, y])
12.1 ms ± 199 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
In [12]: %timeit dstack_product(x, y)
12.7 ms ± 334 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

comme avant, dstack_product bat encore cartesian à des échelles plus petites.

nouvel essai ( ancien essai redondant non montré )

In [13]: x, y = numpy.arange(100), numpy.arange(100)
In [14]: %timeit cartesian([x, y])
215 µs ± 4.75 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [15]: %timeit dstack_product(x, y)
65.7 µs ± 1.15 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

ces distinctions sont, je pense, intéressantes et méritent d'être notées; mais elles sont académiques à la fin. Comme les tests au début de cette réponse ont montré, tous de ces versions sont presque toujours plus lents que cartesian_product , défini au tout début de cette réponse-qui est elle-même un peu plus lent que les implémentations les plus rapides parmi les réponses à cette question.

vous pouvez simplement faire la compréhension de liste normale en python

x = numpy.array([1,2,3])
y = numpy.array([4,5])
[[x0, y0] for x0 in x for y0 in y]

qui devrait vous donner

[[1, 4], [1, 5], [2, 4], [2, 5], [3, 4], [3, 5]]

cela m'intéressait aussi et j'ai fait une petite comparaison du rendement, peut-être un peu plus claire que dans la réponse de @senderle.

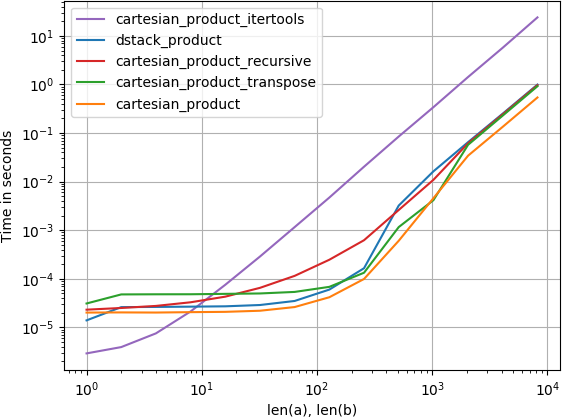
pour deux tableaux (le cas classique):

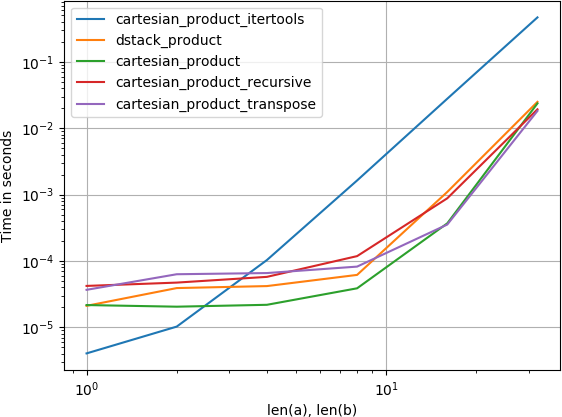
pour quatre tableaux:

(notez que la longueur des tableaux n'est que de quelques dizaines d'entrées ici.)

---

Code pour reproduire les parcelles:

from functools import reduce
import itertools
import numpy
import perfplot


def dstack_product(arrays):
    return numpy.dstack(
        numpy.meshgrid(*arrays, indexing='ij')
        ).reshape(-1, len(arrays))


# Generalized N-dimensional products
def cartesian_product(arrays):
    la = len(arrays)
    dtype = numpy.find_common_type([a.dtype for a in arrays], [])
    arr = numpy.empty([len(a) for a in arrays] + [la], dtype=dtype)
    for i, a in enumerate(numpy.ix_(*arrays)):
        arr[..., i] = a
    return arr.reshape(-1, la)


def cartesian_product_transpose(arrays):
    broadcastable = numpy.ix_(*arrays)
    broadcasted = numpy.broadcast_arrays(*broadcastable)
    rows, cols = reduce(numpy.multiply, broadcasted[0].shape), len(broadcasted)
    dtype = numpy.find_common_type([a.dtype for a in arrays], [])

    out = numpy.empty(rows * cols, dtype=dtype)
    start, end = 0, rows
    for a in broadcasted:
        out[start:end] = a.reshape(-1)
        start, end = end, end + rows
    return out.reshape(cols, rows).T


# from https://stackoverflow.com/a/1235363/577088
def cartesian_product_recursive(arrays, out=None):
    arrays = [numpy.asarray(x) for x in arrays]
    dtype = arrays[0].dtype

    n = numpy.prod([x.size for x in arrays])
    if out is None:
        out = numpy.zeros([n, len(arrays)], dtype=dtype)

    m = n // arrays[0].size
    out[:, 0] = numpy.repeat(arrays[0], m)
    if arrays[1:]:
        cartesian_product_recursive(arrays[1:], out=out[0:m, 1:])
        for j in range(1, arrays[0].size):
            out[j*m:(j+1)*m, 1:] = out[0:m, 1:]
    return out


def cartesian_product_itertools(arrays):
    return numpy.array(list(itertools.product(*arrays)))


perfplot.show(
    setup=lambda n: 4*(numpy.arange(n, dtype=float),),
    n_range=[2**k for k in range(6)],
    kernels=[
        dstack_product,
        cartesian_product,
        cartesian_product_transpose,
        cartesian_product_recursive,
        cartesian_product_itertools
        ],
    logx=True,
    logy=True,
    xlabel='len(a), len(b)',
    equality_check=None
    )

en me basant sur le travail exemplaire de @senderle sur le terrain, j'ai trouvé deux versions - une pour les mises en page C et L'autre pour les mises en page Fortran - qui sont souvent un peu plus rapides.

• cartesian_product_transpose_pp est - contrairement à cartesian_product_transpose de @senderle qui utilise une stratégie tout à fait différente - une version de cartesion_product qui utilise la disposition de la mémoire de transposition plus favorable + quelques optimisations très mineures.
• cartesian_product_pp colle avec la mise en page mémoire originale. Quel le rend rapide est son utilisation de copie contiguë. Les copies contiguës s'avèrent être tellement plus rapides que Copier un bloc complet de mémoire, même si seulement une partie de celui-ci contient des données valides, est préférable à seulement copier les bits valides.

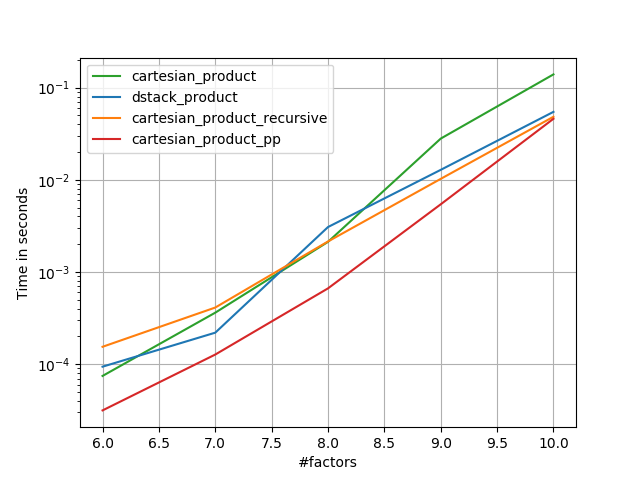
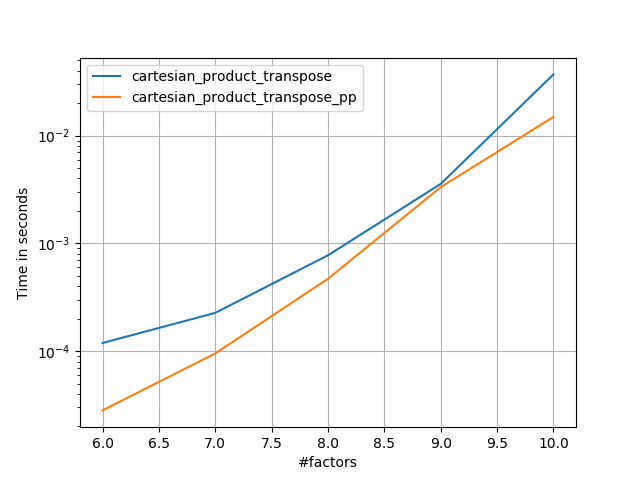
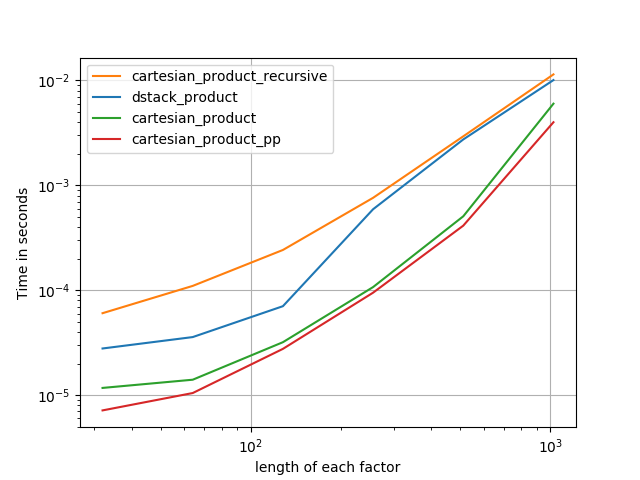
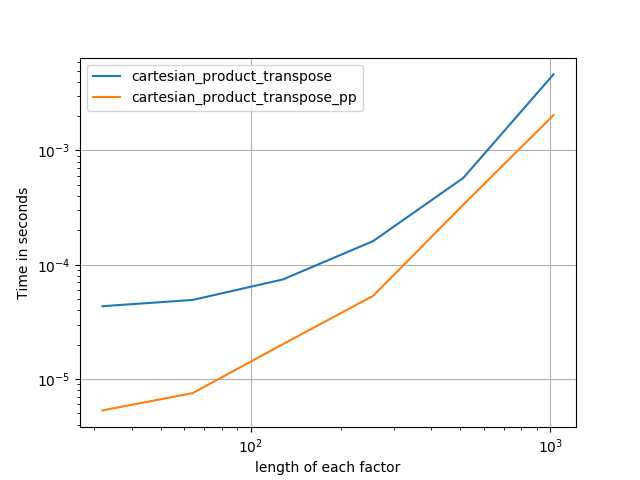
Certains perfplots. J'en ai fait des différents pour C et Fortran layouts, parce que ce sont des tâches différentes IMO.

les noms se terminant en' pp ' sont mes approches.

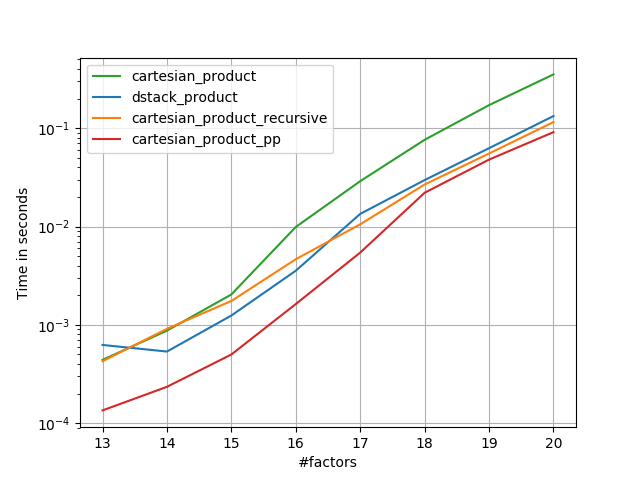
1) de nombreux facteurs minuscules (2 éléments chacun)

2) Beaucoup de petits facteurs (4 éléments chacun)

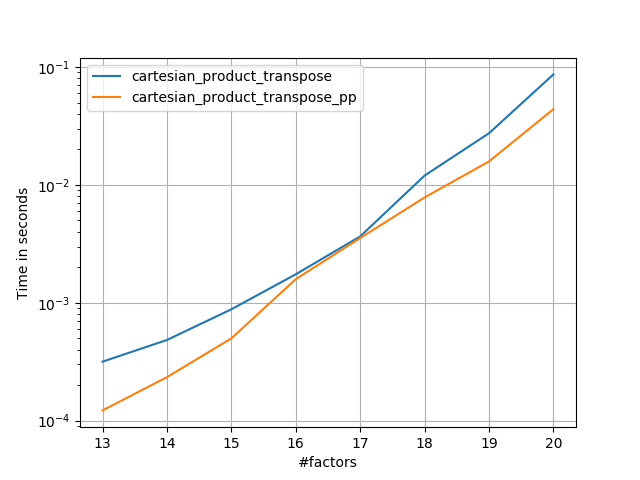
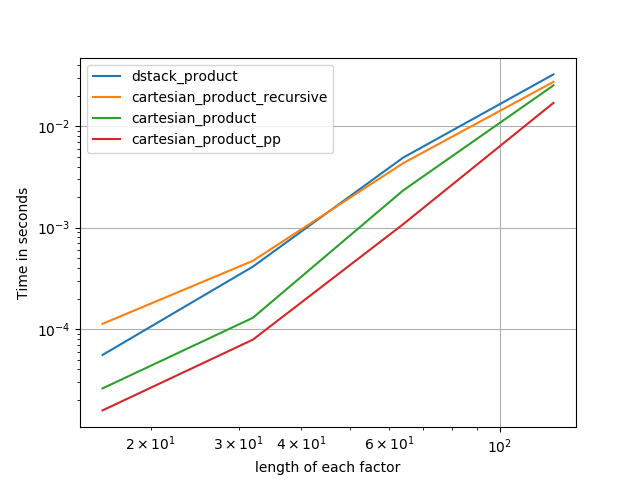
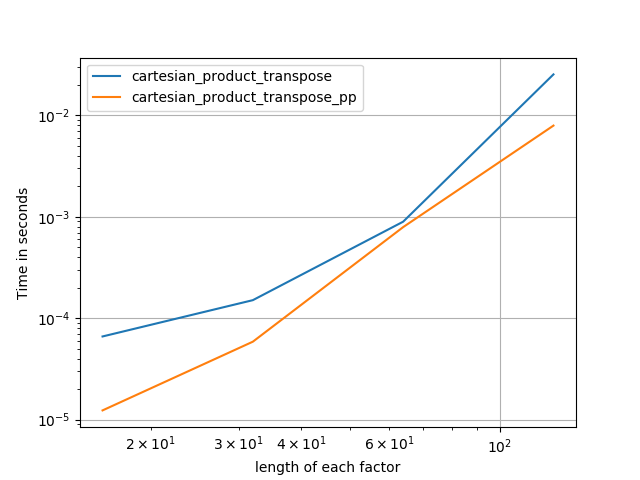
3 )trois facteurs de longueur égale

4 )deux facteurs de longueur égale

Code

(besoin de faire des passages séparés pour chaque parcelle b / c Je n'ai pas pu trouver comment réinitialiser; aussi besoin d'éditer / commenter de façon appropriée):

import numpy
import numpy as np
from functools import reduce
import itertools
import timeit
import perfplot

def dstack_product(arrays):
    return numpy.dstack(
        numpy.meshgrid(*arrays, indexing='ij')
        ).reshape(-1, len(arrays))

def cartesian_product_transpose_pp(arrays):
    la = len(arrays)
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty((la, *map(len, arrays)), dtype=dtype)
    idx = slice(None), *itertools.repeat(None, la)
    for i, a in enumerate(arrays):
        arr[i, ...] = a[idx[:la-i]]
    return arr.reshape(la, -1).T

def cartesian_product(arrays):
    la = len(arrays)
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty([len(a) for a in arrays] + [la], dtype=dtype)
    for i, a in enumerate(numpy.ix_(*arrays)):
        arr[...,i] = a
    return arr.reshape(-1, la)

def cartesian_product_transpose(arrays):
    broadcastable = numpy.ix_(*arrays)
    broadcasted = numpy.broadcast_arrays(*broadcastable)
    rows, cols = numpy.prod(broadcasted[0].shape), len(broadcasted)
    dtype = numpy.result_type(*arrays)

    out = numpy.empty(rows * cols, dtype=dtype)
    start, end = 0, rows
    for a in broadcasted:
        out[start:end] = a.reshape(-1)
        start, end = end, end + rows
    return out.reshape(cols, rows).T

from itertools import accumulate, repeat, chain

def cartesian_product_pp(arrays, out=None):
    la = len(arrays)
    L = *map(len, arrays), la
    dtype = numpy.result_type(*arrays)
    arr = numpy.empty(L, dtype=dtype)
    arrs = *accumulate(chain((arr,), repeat(0, la-1)), np.ndarray.__getitem__),
    idx = slice(None), *itertools.repeat(None, la-1)
    for i in range(la-1, 0, -1):
        arrs[i][..., i] = arrays[i][idx[:la-i]]
        arrs[i-1][1:] = arrs[i]
    arr[..., 0] = arrays[0][idx]
    return arr.reshape(-1, la)

def cartesian_product_itertools(arrays):
    return numpy.array(list(itertools.product(*arrays)))


# from https://stackoverflow.com/a/1235363/577088
def cartesian_product_recursive(arrays, out=None):
    arrays = [numpy.asarray(x) for x in arrays]
    dtype = arrays[0].dtype

    n = numpy.prod([x.size for x in arrays])
    if out is None:
        out = numpy.zeros([n, len(arrays)], dtype=dtype)

    m = n // arrays[0].size
    out[:, 0] = numpy.repeat(arrays[0], m)
    if arrays[1:]:
        cartesian_product_recursive(arrays[1:], out=out[0:m, 1:])
        for j in range(1, arrays[0].size):
            out[j*m:(j+1)*m, 1:] = out[0:m, 1:]
    return out

### Test code ###
if False:
  perfplot.save('cp_4el_high.png',
    setup=lambda n: n*(numpy.arange(4, dtype=float),),
                n_range=list(range(6, 11)),
    kernels=[
        dstack_product,
        cartesian_product_recursive,
        cartesian_product,
#        cartesian_product_transpose,
        cartesian_product_pp,
#        cartesian_product_transpose_pp,
        ],
    logx=False,
    logy=True,
    xlabel='#factors',
    equality_check=None
    )
else:
  perfplot.save('cp_2f_T.png',
    setup=lambda n: 2*(numpy.arange(n, dtype=float),),
    n_range=[2**k for k in range(5, 11)],
    kernels=[
#        dstack_product,
#        cartesian_product_recursive,
#        cartesian_product,
        cartesian_product_transpose,
#        cartesian_product_pp,
        cartesian_product_transpose_pp,
        ],
    logx=True,
    logy=True,
    xlabel='length of each factor',
    equality_check=None
    )

en date du 1er Oct. 2017, numpy a maintenant une fonction générique np.stack qui prend un paramètre axis. En l'utilisant, Nous pouvons avoir un "produit cartésien généralisé" en utilisant la technique "dstack et meshgrid":

import numpy as np
def cartesian_product(*arrays):
    ndim = len(arrays)
    return np.stack(np.meshgrid(*arrays), axis=-1).reshape(-1, ndim)

Note sur le paramètre axis=-1 . C'est le dernier axe (interne-le plus) du résultat. Il est équivalent à axis=ndim .

un autre commentaire, car les produits cartésiens explosent très vite, à moins que nous ne soyons besoin pour réaliser le tableau en mémoire pour une raison quelconque, si le produit est très grand, nous pouvons vouloir faire usage de itertools et utiliser les valeurs à la volée.

j'ai utilisé @kennytm réponse pendant un certain temps, mais en essayant de faire la même chose dans TensorFlow, mais j'ai trouvé que TensorFlow n'a pas l'équivalent de numpy.repeat() . Après un peu d'expérimentation, je pense que j'ai trouvé une solution plus générale pour les vecteurs arbitraires de points.

pour numpy:

import numpy as np

def cartesian_product(*args: np.ndarray) -> np.ndarray:
    """
    Produce the cartesian product of arbitrary length vectors.

    Parameters
    ----------
    np.ndarray args
        vector of points of interest in each dimension

    Returns
    -------
    np.ndarray
        the cartesian product of size [m x n] wherein:
            m = prod([len(a) for a in args])
            n = len(args)
    """
    for i, a in enumerate(args):
        assert a.ndim == 1, "arg {:d} is not rank 1".format(i)
    return np.concatenate([np.reshape(xi, [-1, 1]) for xi in np.meshgrid(*args)], axis=1)

et pour TensorFlow:

import tensorflow as tf

def cartesian_product(*args: tf.Tensor) -> tf.Tensor:
    """
    Produce the cartesian product of arbitrary length vectors.

    Parameters
    ----------
    tf.Tensor args
        vector of points of interest in each dimension

    Returns
    -------
    tf.Tensor
        the cartesian product of size [m x n] wherein:
            m = prod([len(a) for a in args])
            n = len(args)
    """
    for i, a in enumerate(args):
        tf.assert_rank(a, 1, message="arg {:d} is not rank 1".format(i))
    return tf.concat([tf.reshape(xi, [-1, 1]) for xi in tf.meshgrid(*args)], axis=1)

le Scikit-learn paquet a une mise en œuvre rapide de exactement cela:

from sklearn.utils.extmath import cartesian
product = cartesian((x,y))

notez que la convention de cette implémentation est différente de ce que vous voulez, si vous vous souciez de l'ordre de la sortie. Pour votre commande exacte, vous pouvez faire

product = cartesian((y,x))[:, ::-1]

plus généralement, si vous avez deux tableaux 2D vides a et b, et que vous voulez concaténer chaque ligne de a à chaque ligne de b (Un produit cartésien de lignes, un peu comme une jointure dans une base de données), vous pouvez utiliser cette méthode:

import numpy
def join_2d(a, b):
    assert a.dtype == b.dtype
    a_part = numpy.tile(a, (len(b), 1))
    b_part = numpy.repeat(b, len(a), axis=0)
    return numpy.hstack((a_part, b_part))

le plus rapide que vous pouvez obtenir est soit en combinant une expression de générateur avec la fonction de carte:

import numpy
import datetime
a = np.arange(1000)
b = np.arange(200)

start = datetime.datetime.now()

foo = (item for sublist in [list(map(lambda x: (x,i),a)) for i in b] for item in sublist)

print (list(foo))

print ('execution time: {} s'.format((datetime.datetime.now() - start).total_seconds()))

sorties (en fait toute la liste résultante est imprimée):

[(0, 0), (1, 0), ...,(998, 199), (999, 199)]
execution time: 1.253567 s

ou en utilisant l'expression d'un double générateur:

a = np.arange(1000)
b = np.arange(200)

start = datetime.datetime.now()

foo = ((x,y) for x in a for y in b)

print (list(foo))

print ('execution time: {} s'.format((datetime.datetime.now() - start).total_seconds()))

sorties (liste complète imprimée):

[(0, 0), (1, 0), ...,(998, 199), (999, 199)]
execution time: 1.187415 s

tient compte du fait que la plus grande partie du temps de calcul entre dans la commande d'impression. Le les calculs du générateur sont par ailleurs décemment efficaces. Sans impression, les temps de calcul sont:

execution time: 0.079208 s

pour Expression génératrice + fonction de carte et:

execution time: 0.007093 s

pour l'expression de générateur double.

Si ce que vous voulez vraiment est de calculer le produit de chacune des paires de coordonnées, le plus rapide est de résoudre comme numpy produit matriciel:

a = np.arange(1000)
b = np.arange(200)

start = datetime.datetime.now()

foo = np.dot(np.asmatrix([[i,0] for i in a]), np.asmatrix([[i,0] for i in b]).T)

print (foo)

print ('execution time: {} s'.format((datetime.datetime.now() - start).total_seconds()))

Sorties

:

 [[     0      0      0 ...,      0      0      0]
 [     0      1      2 ...,    197    198    199]
 [     0      2      4 ...,    394    396    398]
 ..., 
 [     0    997   1994 ..., 196409 197406 198403]
 [     0    998   1996 ..., 196606 197604 198602]
 [     0    999   1998 ..., 196803 197802 198801]]
execution time: 0.003869 s

et sans impression (dans ce cas, il n'économise pas beaucoup car seul un petit morceau de la matrice est effectivement imprimé):

execution time: 0.003083 s

Cela peut aussi être fait facilement en utilisant itertools.méthode du produit

from itertools import product
import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5])
cart_prod = np.array(list(product(*[[x], [y]])),dtype='int32')

résultat: tableau([

[1, 4],

[1, 5],

[2, 4],

[2, 5],

[3, 4],

[3, 5]], dtype=int32)

délai d'exécution: 0.000155 s