test de normalité d'une distribution en python
j'ai quelques données que j'ai échantillonnées à partir d'une image satellite radar et je voulais effectuer quelques tests statistiques sur. Avant cela, je voulais faire un test de normalité pour être sûr que mes données étaient distribuées normalement. Mes données semblent être distribuées normalement, mais lorsque j'effectue le test, J'obtiens une valeur de P de 0, ce qui suggère que mes données ne sont pas distribuées normalement.
j'ai joint mon code avec la sortie et un histogramme de la distribution (Im relativement python donc toutes mes excuses si mon code est maladroit, en quelque sorte). Est - ce que quelqu'un peut me dire si je fais quelque chose de mal-j'ai du mal à croire de mon histogramme que mes données ne sont pas normalement distribuées?
values = 'inputfile.h5'
f = h5py.File(values,'r')
dset = f['/DATA/DATA']
array = dset[...,0]
print('normality =', scipy.stats.normaltest(array))
max = np.amax(array)
min = np.amin(array)
histo = np.histogram(array, bins=100, range=(min, max))
freqs = histo[0]
rangebins = (max - min)
numberbins = (len(histo[1])-1)
interval = (rangebins/numberbins)
newbins = np.arange((min), (max), interval)
histogram = bar(newbins, freqs, width=0.2, color='gray')
plt.show()
ceci imprime ceci: (41099.095955202931, 0.0). le premier élément est une valeur de chi carré et le second est une valeur de P.
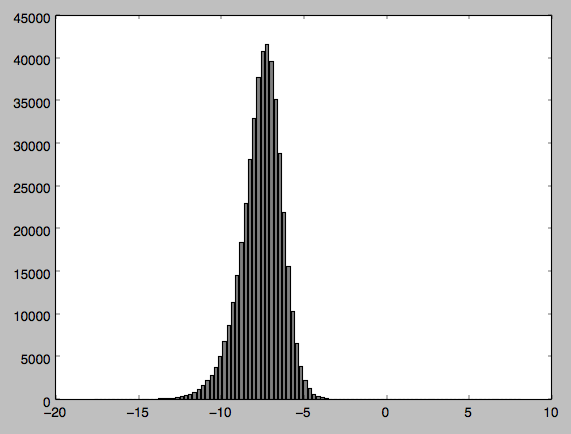
j'ai fait un graphique des données que j'ai joint. J'ai pensé que peut-être comme je traite avec des valeurs négatives il causait un problème alors j'ai normalisé les valeurs mais le problème persiste.
2 réponses
en général, lorsque le nombre d'échantillons est inférieur à 50, vous devez faire attention à ne pas utiliser des tests de normalité. Puisque ces tests ont besoin de suffisamment de preuves pour rejeter l'hypothèse nulle, qui est "la distribution des données est normale", et quand le nombre d'échantillons est petit, ils ne sont pas en mesure de trouver ces preuves.
Conserver à l'esprit que lorsque vous ne pouvez pas rejeter l'hypothèse nulle, cela ne signifie pas que l'hypothèse alternative est correct.
Il y a un autre possibilité que: Certaines implémentations des tests statistiques pour la normalité comparent la distribution de vos données à la distribution normale standard. Pour éviter cela, je vous suggère de normaliser les données et ensuite d'appliquer le test de normalité.
cette question explique pourquoi vous obtenez un si petit p-valeur. Essentiellement, les tests de normalité rejettent presque toujours le nul sur les très grandes tailles d'échantillon (dans le vôtre, par exemple, vous pouvez voir juste une certaine asymétrie dans le côté gauche, qui à votre taille d'échantillon énorme est beaucoup plus qu'assez).
Ce serait beaucoup plus pratique, utile dans votre cas est de tracer une courbe normale ajustement de vos données. Ensuite, vous pouvez voir comment la courbe normale diffère en fait (par exemple, vous pouvez voir si la queue sur le côté gauche, en effet, passer trop de temps). Par exemple:
from matplotlib import pyplot as plt
import matplotlib.mlab as mlab
n, bins, patches = plt.hist(array, 50, normed=1)
mu = np.mean(array)
sigma = np.std(array)
plt.plot(bins, mlab.normpdf(bins, mu, sigma))
(normed=1 argument: cela garantit que l'histogramme est normalisé pour une superficie totale de 1, ce qui le rend comparable à une densité comme la distribution normale).