Poids négatifs à L'aide de L'algorithme de Dijkstra

j'essaie de comprendre pourquoi L'algorithme de Dijkstra ne fonctionne pas avec des poids négatifs. En lisant un exemple sur les chemins Les plus courts , j'essaie de comprendre le scénario suivant: 

    2
A-------B
      /
3    / -2
    /
    C

sur le site:

en supposant que les bords sont tous dirigés de gauche à droite, si nous commençons avec A, L'algorithme de Dijkstra choisira le bord (a, x) minimisant d(A, A)+Longueur (bord), à savoir (A, B). Il puis définit d (A, B)=2 et choisit un autre bord (y,C) minimisant d (A,y)+d (y,C); le seul choix est (A, C) et il est d (A, C)=3. Mais il ne trouve jamais le chemin le plus court d'un à B, via C, avec longueur totale 1.

Je ne peux pas comprendre pourquoi en utilisant L'implémentation suivante de Dijkstra, d[B] ne sera pas mis à jour à 1 (lorsque l'algorithme atteint vertex C, il exécutera un relax sur B, voir que le d[B] est égal à 2 , et donc mettre à jour son valeur à 1 ). 

Dijkstra(G, w, s)  {
   Initialize-Single-Source(G, s)
   S ← Ø
   Q ← V[G]//priority queue by d[v]
   while Q ≠ Ø do
      u ← Extract-Min(Q)
      S ← S U {u}
      for each vertex v in Adj[u] do
         Relax(u, v)
}

Initialize-Single-Source(G, s) {
   for each vertex v  V(G)
      d[v] ← ∞
      π[v] ← NIL
   d[s] ← 0
}

Relax(u, v) {
   //update only if we found a strictly shortest path
   if d[v] > d[u] + w(u,v) 
      d[v] ← d[u] + w(u,v)
      π[v] ← u
      Update(Q, v)
}

Merci,

Meir

101
demandé sur templatetypedef 2011-07-23 12:19:14

6 réponses

l'algorithme que vous avez suggéré trouvera en effet le chemin le plus court dans ce graphique, mais pas tous les graphiques en général. Par exemple, considérons ce graphique:

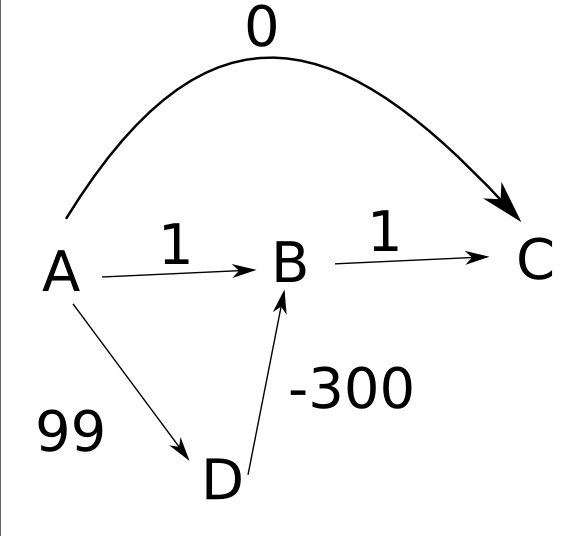
Figure of graph

supposons que les bords sont dirigés de gauche à droite comme dans votre exemple,

votre algorithme fonctionnera comme suit:

  1. D'abord, vous mettez d(A) à zero et les autres distances à infinity .
  2. vous étendez alors le noeud A , en mettant d(B) à 1 , d(C) à zero , et d(D) à 99 .
  3. Ensuite, vous développez C , sans variations nettes.
  4. vous étendez alors B , ce qui n'a pas d'effet.
  5. enfin, vous étendez D , qui change d(B) en -201 .

notez qu'à la fin de ceci, cependant, que d(C) est toujours 0 , même si le chemin le plus court vers C a la longueur -200 . votre algorithme ne calcule donc pas correctement les distances dans certains cas. En outre, même si vous deviez stocker des pointeurs arrière disant comment aller de chaque noeud au noeud de départ A , vous finiriez par prendre le mauvais chemin de retour de C à A .

177
répondu templatetypedef 2014-05-10 08:18:25

noter, que Dijkstra fonctionne même pour les poids négatifs, si le graphique n'a pas de cycles négatifs, c.-à-d. les cycles dont le poids total est inférieur à zéro.

bien sûr, on pourrait se demander, pourquoi dans l'exemple fait par templatetypedef Dijkstra échoue bien qu'il n'y ait pas de cycles négatifs, en fait pas même des cycles. C'est parce qu'il utilise un autre critère d'arrêt, qui retient l'algorithme dès que le nœud cible est atteinte (ou tous les nœuds ont été réglées une fois, il n'a pas spécifier exactement). Dans un graphique sans poids négatifs cela fonctionne très bien.

si l'on utilise le critère d'arrêt alternatif, qui arrête l'algorithme lorsque la file d'attente prioritaire (tas) est vide (ce critère d'arrêt a également été utilisé dans la question), alors dijkstra trouvera la bonne distance même pour les graphiques avec des poids négatifs mais sans cycles négatifs.

cependant, dans ce cas, la limite de temps asymptotique de dijkstra pour les graphiques sans cycles négatifs perdus. Ceci est dû au fait qu'un noeud déjà réglé peut être réinséré dans le tas lorsqu'une meilleure distance est trouvée due à des poids négatifs. Cette propriété est appelée correction d'étiquette.

18
répondu infty10000101 2014-08-06 13:06:24

vous n'avez utilisé S nulle part dans votre algorithme (en plus de le modifier). l'idée de dijkstra est une fois qu'un vertex est sur S, il ne sera plus jamais modifié. dans ce cas, une fois que B est à L'intérieur de S, vous ne l'atteindrez plus via C.

ce fait assure la complexité de O (E+VlogV) [sinon, vous répéterez les arêtes plus d'une fois, et les sommets plus d'une fois]

en d'autres termes, l'algorithme que vous avez posté, pourrait ne pas être en O(E+VlogV), comme promis par l'algorithme de dijkstra.

8
répondu amit 2011-07-23 09:07:14

puisque Dijkstra est une approche gourmande, une fois qu'un vertice est marqué comme visité pour cette boucle, il ne serait jamais réévalué à nouveau, même s'il y a un autre chemin avec moins de coût pour l'atteindre plus tard. Et un tel problème ne pourrait se produire que lorsque des bords négatifs existent dans le graphique.

Un algorithme glouton , comme son nom l'indique, toujours fait le choix qui me semble être le meilleur à ce moment-là. supposons que vous avez une fonction objective qui doit être optimisée (soit maximisée ou minimisée) à un point donné. un algorithme gourmand fait des choix gourmands à chaque étape pour s'assurer que la fonction d'objectif est optimisée. l'algorithme de Greedy n'a qu'un seul essai pour calculer la solution optimale de sorte que il ne va jamais en arrière et inverse la décision.

6
répondu punchoyeah 2017-05-29 01:58:27

pensez à ce qui se passe si vous faites des allers - retours entre B et C...voilà

(applicable seulement si le graphique n'est pas dirigé)

édité: Je crois que le problème est lié au fait que le chemin avec AC* ne peut être meilleur que AB avec l'existence de bords de poids négatifs, de sorte qu'il n'importe pas où vous allez après AC, avec l'hypothèse de bords de poids non négatifs, il est impossible de trouver un chemin meilleur que AB une fois que vous avez choisi d'atteindre B après avoir AC.

1
répondu prusswan 2011-07-23 09:04:39

" 2) Pouvons – nous utiliser L'algorithme de Dijksra pour les chemins Les plus courts pour les graphiques avec des poids négatifs-une idée peut être, calculer la valeur de poids minimum, ajouter une valeur positive (égale à la valeur absolue de la valeur de poids minimum) à tous les poids et exécuter l'algorithme de Dijksra pour le graphique modifié. Sera-ce l'algorithme de travail?"

cela ne fonctionne absolument pas à moins que tous les chemins Les plus courts aient la même longueur. Par exemple donné un chemin le plus court de la longueur deux bords, et après avoir ajouté valeur absolue à chaque bord, puis le coût total du sillon est augmenté de 2 * / poids négatif max/. D'autre part, un autre chemin de longueur trois bords, de sorte que le coût du chemin est augmenté de 3 * |max poids négatif|. Par conséquent, tous les chemins distincts sont augmentés de différentes quantités.

1
répondu Wackyfool 2017-05-22 17:20:18