intervalles de confiance multidimensionnels
j'ai de nombreux tuples (par1,par2), c'est-à-dire des points dans un espace de paramètre bidimensionnel obtenu en répétant plusieurs fois une expérience.
je cherche une possibilité de calculer et de visualiser des ellipses de confiance (pas sûr si c'est le terme correct pour cela). Voici un exemple de graphique que j'ai trouvé dans le web pour montrer ce que je veux dire:
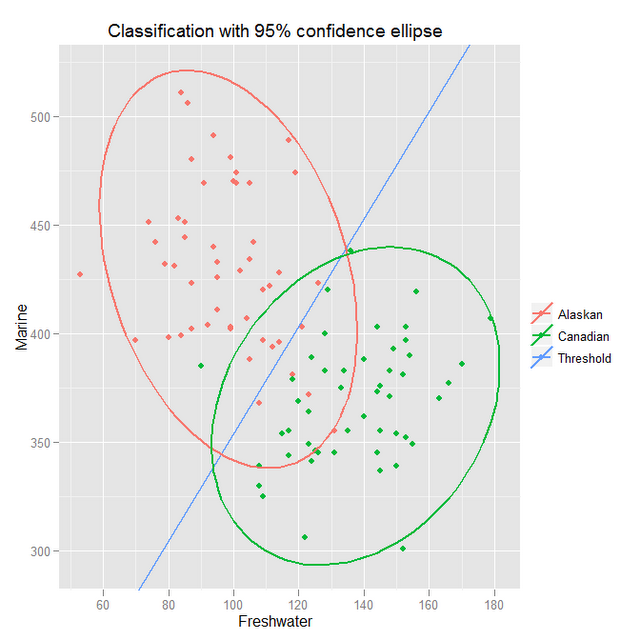
source: blogspot.ch/2011/07/classification-and-discrimination-with.html
Donc en principe, on doit ajuster une distribution normale multivariée à un histogramme 2D de points de données je suppose. Quelqu'un peut-il m'aider?
4 réponses
on dirait que vous voulez juste l'ellipse 2-sigma de la dispersion des points?
Si oui, pensez à quelque chose comme ceci (à Partir d'un code pour un papier ici: https://github.com/joferkington/oost_paper_code/blob/master/error_ellipse.py):
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
def plot_point_cov(points, nstd=2, ax=None, **kwargs):
"""
Plots an `nstd` sigma ellipse based on the mean and covariance of a point
"cloud" (points, an Nx2 array).
Parameters
----------
points : An Nx2 array of the data points.
nstd : The radius of the ellipse in numbers of standard deviations.
Defaults to 2 standard deviations.
ax : The axis that the ellipse will be plotted on. Defaults to the
current axis.
Additional keyword arguments are pass on to the ellipse patch.
Returns
-------
A matplotlib ellipse artist
"""
pos = points.mean(axis=0)
cov = np.cov(points, rowvar=False)
return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)
def plot_cov_ellipse(cov, pos, nstd=2, ax=None, **kwargs):
"""
Plots an `nstd` sigma error ellipse based on the specified covariance
matrix (`cov`). Additional keyword arguments are passed on to the
ellipse patch artist.
Parameters
----------
cov : The 2x2 covariance matrix to base the ellipse on
pos : The location of the center of the ellipse. Expects a 2-element
sequence of [x0, y0].
nstd : The radius of the ellipse in numbers of standard deviations.
Defaults to 2 standard deviations.
ax : The axis that the ellipse will be plotted on. Defaults to the
current axis.
Additional keyword arguments are pass on to the ellipse patch.
Returns
-------
A matplotlib ellipse artist
"""
def eigsorted(cov):
vals, vecs = np.linalg.eigh(cov)
order = vals.argsort()[::-1]
return vals[order], vecs[:,order]
if ax is None:
ax = plt.gca()
vals, vecs = eigsorted(cov)
theta = np.degrees(np.arctan2(*vecs[:,0][::-1]))
# Width and height are "full" widths, not radius
width, height = 2 * nstd * np.sqrt(vals)
ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs)
ax.add_artist(ellip)
return ellip
if __name__ == '__main__':
#-- Example usage -----------------------
# Generate some random, correlated data
points = np.random.multivariate_normal(
mean=(1,1), cov=[[0.4, 9],[9, 10]], size=1000
)
# Plot the raw points...
x, y = points.T
plt.plot(x, y, 'ro')
# Plot a transparent 3 standard deviation covariance ellipse
plot_point_cov(points, nstd=3, alpha=0.5, color='green')
plt.show()
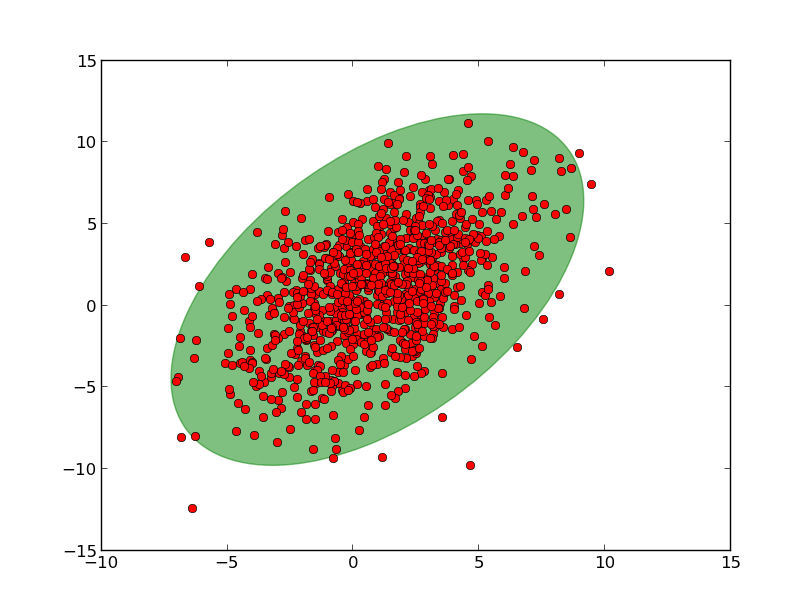
Consulter le post comment dessiner une ellipse d'erreur de covariance.
Voici la réalisation de python:
import numpy as np
from scipy.stats import norm, chi2
def cov_ellipse(cov, q=None, nsig=None, **kwargs):
"""
Parameters
----------
cov : (2, 2) array
Covariance matrix.
q : float, optional
Confidence level, should be in (0, 1)
nsig : int, optional
Confidence level in unit of standard deviations.
E.g. 1 stands for 68.3% and 2 stands for 95.4%.
Returns
-------
width, height, rotation :
The lengths of two axises and the rotation angle in degree
for the ellipse.
"""
if q is not None:
q = np.asarray(q)
elif nsig is not None:
q = 2 * norm.cdf(nsig) - 1
else:
raise ValueError('One of `q` and `nsig` should be specified.')
r2 = chi2.ppf(q, 2)
val, vec = np.linalg.eigh(cov)
width, height = 2 * sqrt(val[:, None] * r2)
rotation = np.degrees(arctan2(*vec[::-1, 0]))
return width, height, rotation
La signification de écart-typemauvais dans la réponse de Joe Kington. Habituellement, nous utilisons 1, 2 sigma pour 68%, 95% des niveaux de confiance, mais l'ellipse de 2 sigma dans sa réponse ne contient pas 95% de probabilité de la distribution totale. La bonne façon est d'utiliser une distribution de chi carré pour simuler la taille de l'ellipse comme indiqué dans le post.
j'ai légèrement modifié un des exemples ci-dessus qui tracent les contours de la région d'erreur ou de confiance. Maintenant je pense que ça donne les bons contours.
il donnait les mauvais contours parce qu'il appliquait la méthode du percentile de la carte de pointage à l'ensemble de données commun (points bleus + rouges) quand il devrait être appliqué séparément à chaque ensemble de données.
Le code modifié peut être trouvé ci-dessous:
import numpy
import scipy
import scipy.stats
import matplotlib.pyplot as plt
# generate two normally distributed 2d arrays
x1=numpy.random.multivariate_normal((100,420),[[120,80],[80,80]],400)
x2=numpy.random.multivariate_normal((140,340),[[90,-70],[-70,80]],400)
# fit a KDE to the data
pdf1=scipy.stats.kde.gaussian_kde(x1.T)
pdf2=scipy.stats.kde.gaussian_kde(x2.T)
# create a grid over which we can evaluate pdf
q,w=numpy.meshgrid(range(50,200,10), range(300,500,10))
r1=pdf1([q.flatten(),w.flatten()])
r2=pdf2([q.flatten(),w.flatten()])
# sample the pdf and find the value at the 95th percentile
s1=scipy.stats.scoreatpercentile(pdf1(pdf1.resample(1000)), 5)
s2=scipy.stats.scoreatpercentile(pdf2(pdf2.resample(1000)), 5)
# reshape back to 2d
r1.shape=(20,15)
r2.shape=(20,15)
# plot the contour at the 95th percentile
plt.contour(range(50,200,10), range(300,500,10), r1, [s1],colors='b')
plt.contour(range(50,200,10), range(300,500,10), r2, [s2],colors='r')
# scatter plot the two normal distributions
plt.scatter(x1[:,0],x1[:,1],alpha=0.3)
plt.scatter(x2[:,0],x2[:,1],c='r',alpha=0.3)
je suppose que ce que vous cherchez est de calculer l' Régions De Confiance.
Je ne sais pas grand chose à ce sujet, mais comme point de départ, je vérifierais le sherpa application pour python. Au moins, dans leur exposé de Scipy 2011, les auteurs mentionnent que vous pouvez déterminer et obtenir des régions de confiance avec elle (vous pourriez avoir besoin d'un modèle pour vos données cependant).
voir le vidéo et correspondant diapositives de la Sherpa talk.
HTH