Monte Carlo Tree Search: implémentation pour Tic-Tac-Toe

Edit: Uploded la totalité du code source si vous voulez voir si vous pouvez obtenir de l'IA pour mieux performer: https://www.dropbox.com/s/ous72hidygbnqv6/MCTS_TTT.rar

Edit: l'espace de recherche est recherché et les mouvements entraînant des pertes sont trouvés. Mais les mouvements entraînant des pertes ne sont pas visités très souvent à cause de l'algorithme UCT.

pour en savoir plus sur les MCTS (Monte Carlo Tree Search) j'ai utilisé l'algorithme pour faire une IA pour le jeu classique de tic-tac-toe. J'ai mise en œuvre de l'algorithme à l'aide de la structure suivante:

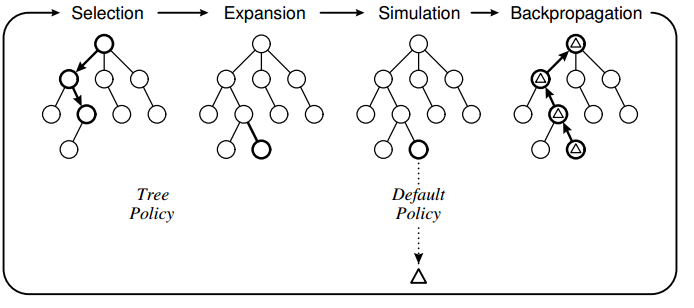La Politique de tree est basée sur UCT et la politique par défaut est d'effectuer des mouvements aléatoires jusqu'à la fin du jeu. Ce que j'ai observé avec mon implémentation, c'est que l'ordinateur fait parfois des mouvements errorés parce qu'il ne "voit" pas qu'un mouvement particulier entraînera une perte directe.

Par exemple: 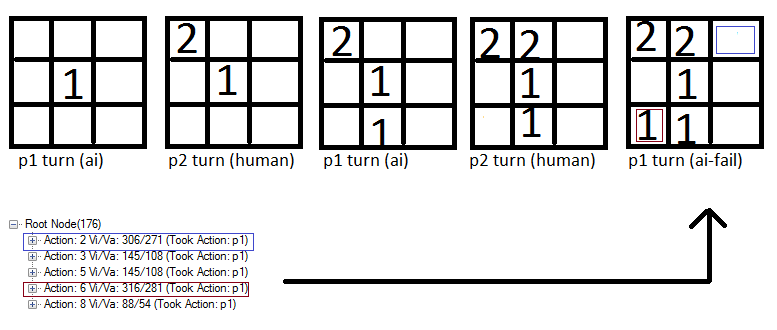Notez comment l'action 6 (carré rouge) est évaluée légèrement plus haut que le bleu carré et donc l'ordinateur Marque cet endroit. Je pense que c'est parce que la Politique de jeu est basée sur des mouvements aléatoires et donc une bonne chance existe que l'humain ne mettra pas un "2" dans la boîte bleue. Et si le joueur ne met pas un 2 dans la boîte bleue, l'ordinateur est gaurented une victoire.

Mes Questions

1) s'agit-il d'un problème connu des SCTM ou est-ce le résultat d'une mise en œuvre ratée?

2) Quelles sont les solutions possibles? Je suis penser à limiter les mouvements dans la phase de sélection mais je ne suis pas sûr: -)

Le code du noyau des SCTM:

    //THE EXECUTING FUNCTION
    public unsafe byte GetBestMove(Game game, int player, TreeView tv)
    {

        //Setup root and initial variables
        Node root = new Node(null, 0, Opponent(player));
        int startPlayer = player;

        helper.CopyBytes(root.state, game.board);

        //four phases: descent, roll-out, update and growth done iteratively X times
        //-----------------------------------------------------------------------------------------------------
        for (int iteration = 0; iteration < 1000; iteration++)
        {
            Node current = Selection(root, game);
            int value = Rollout(current, game, startPlayer);
            Update(current, value);
        }

        //Restore game state and return move with highest value
        helper.CopyBytes(game.board, root.state);

        //Draw tree
        DrawTree(tv, root);

        //return root.children.Aggregate((i1, i2) => i1.visits > i2.visits ? i1 : i2).action;
        return BestChildUCB(root, 0).action;
    }

    //#1. Select a node if 1: we have more valid feasible moves or 2: it is terminal 
    public Node Selection(Node current, Game game)
    {
        while (!game.IsTerminal(current.state))
        {
            List<byte> validMoves = game.GetValidMoves(current.state);

            if (validMoves.Count > current.children.Count)
                return Expand(current, game);
            else
                current = BestChildUCB(current, 1.44);
        }

        return current;
    }

    //#1. Helper
    public Node BestChildUCB(Node current, double C)
    {
        Node bestChild = null;
        double best = double.NegativeInfinity;

        foreach (Node child in current.children)
        {
            double UCB1 = ((double)child.value / (double)child.visits) + C * Math.Sqrt((2.0 * Math.Log((double)current.visits)) / (double)child.visits);

            if (UCB1 > best)
            {
                bestChild = child;
                best = UCB1;
            }
        }

        return bestChild;
    }

    //#2. Expand a node by creating a new move and returning the node
    public Node Expand(Node current, Game game)
    {
        //Copy current state to the game
        helper.CopyBytes(game.board, current.state);

        List<byte> validMoves = game.GetValidMoves(current.state);

        for (int i = 0; i < validMoves.Count; i++)
        {
            //We already have evaluated this move
            if (current.children.Exists(a => a.action == validMoves[i]))
                continue;

            int playerActing = Opponent(current.PlayerTookAction);

            Node node = new Node(current, validMoves[i], playerActing);
            current.children.Add(node);

            //Do the move in the game and save it to the child node
            game.Mark(playerActing, validMoves[i]);
            helper.CopyBytes(node.state, game.board);

            //Return to the previous game state
            helper.CopyBytes(game.board, current.state);

            return node;
        }

        throw new Exception("Error");
    }

    //#3. Roll-out. Simulate a game with a given policy and return the value
    public int Rollout(Node current, Game game, int startPlayer)
    {
        Random r = new Random(1337);
        helper.CopyBytes(game.board, current.state);
        int player = Opponent(current.PlayerTookAction);

        //Do the policy until a winner is found for the first (change?) node added
        while (game.GetWinner() == 0)
        {
            //Random
            List<byte> moves = game.GetValidMoves();
            byte move = moves[r.Next(0, moves.Count)];
            game.Mark(player, move);
            player = Opponent(player);
        }

        if (game.GetWinner() == startPlayer)
            return 1;

        return 0;
    }

    //#4. Update
    public unsafe void Update(Node current, int value)
    {
        do
        {
            current.visits++;
            current.value += value;
            current = current.parent;
        }
        while (current != null);
    }