Mesure de l'épaisseur moyenne des traces dans une image
Voici le problème: j'ai un certain nombre d'images binaires composées par des traces de différentes épaisseurs. Ci-dessous il y a deux images pour illustrer le problème:
première Image-taille: 711 x 643 px

Deuxième Image - taille: 930 x 951 px

Ce dont j'ai besoin est de mesurer l'épaisseur moyenne (en pixels) des traces dans les images. En fait, l'épaisseur moyenne des traces dans une image est mesure quelque peu subjective. Donc, ce dont j'ai besoin est une mesure qui a une certaine corrélation avec le rayon de la trace, comme indiqué dans la figure ci-dessous:
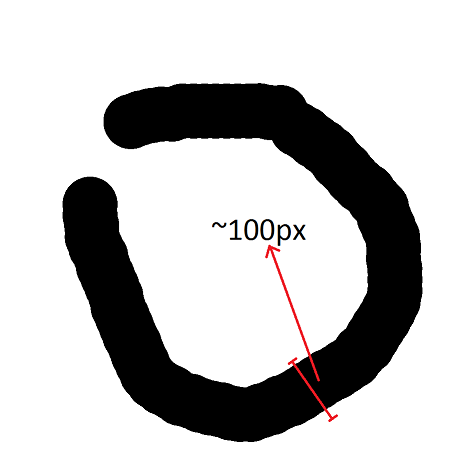
Notes
puisque la mesure n'a pas besoin d'être très précise, je suis prêt à échanger la précision contre la vitesse. En d'autres termes, la vitesse est un facteur important pour résoudre ce problème.
il pourrait y avoir des intersections trace.
l'épaisseur de la trace peut ne pas être constante, mais une mesure moyenne est acceptable (même l'épaisseur maximale de la trace est acceptable).
La trace sera toujours beaucoup plus long que large.
7 réponses
je suggère cet algorithme:
- appliquez une transformation de distance à l'image, de sorte que tous les pixels d'arrière-plan soient positionnés à 0, tous les pixels d'avant-plan sont positionnés à la distance de l'arrière-plan
- trouver les maxima locaux dans l'image transformée de distance. Ce sont des points au milieu des lignes. Mettez leurs valeurs de pixel (i.e. distances de l'image de fond) dans une liste
- Calculer la médiane ou la moyenne de la liste
j'ai été impressionné par la réponse de @nikie, et j'ai essayé ...
j'ai simplifié l'algorithme pour obtenir juste la valeur maximale, pas la moyenne, donc j'élude l'algorithme local de détection de maxima. Je pense que c'est suffisant si l'attaque est bien-comportée (bien que pour auto croisements des lignes il peut ne pas être exact).
m = Import["http://imgur.com/3Zs7m.png"] (* Get image from web*)
s = Abs[ImageData[m] - 1]; (* Invert colors to detect background *)
k = DistanceTransform[Image[s]] (* White Pxs converted to distance to black*)
k // ImageAdjust (* Show the image *)
Max[ImageData[k]] (* Get the max stroke width *)
Le résultat généré est

numérique valeur (28.46 px X 2) correspond assez bien à ma mesure de 56 px (bien que votre valeur soit de 100px:*)
Edit-implémenté l'algorithme complet
Bien ... en quelque sorte ... au lieu de chercher les maxima locaux, trouver le point fixe de la transformation de distance. Presque, mais pas tout à fait à la différence de la même chose :)
m = Import["http://imgur.com/3Zs7m.png"]; (*Get image from web*)
s = Abs[ImageData[m] - 1]; (*Invert colors to detect background*)
k = DistanceTransform[Image[s]]; (*White Pxs converted to distance to black*)
Print["Distance to Background*"]
k // ImageAdjust (*Show the image*)
Print["Local Maxima"]
weights =
Binarize[FixedPoint[ImageAdjust@DistanceTransform[Image[#], .4] &,s]]
Print["Stroke Width =",
2 Mean[Select[Flatten[ImageData[k]] Flatten[ImageData[weights]], # != 0 &]]]
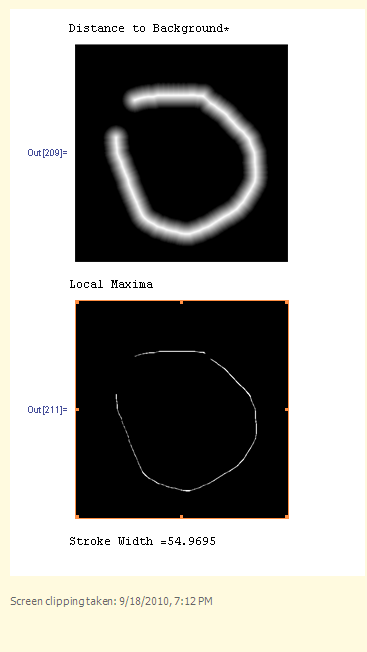
Ici. Une méthode simple!
3.1 Estimation De La Largeur De La Plume
l'épaisseur du stylo peut être facilement estimée à partir de la zone A et de la longueur du périmètre L du premier plan
T = A/(L/2)
essentiellement, nous avons remodelé le premier plan en un rectangle et mesuré la longueur du côté le plus long. Une modélisation plus forte du stylo, par exemple, en tant que disque donnant des extrémités circulaires, pourrait permettre une plus grande précision, mais une erreur de rastérisation à compromettre la signication.
bien que la précision ne soit pas un problème majeur, nous devons tenir compte des biais et des singularités.
il faut donc calculer la zone A et la longueur du périmètre L en utilisant des fonctions qui tiennent compte de "l'arrondi". In MATLAB
A = bwarea(.)
L = bwarea(bwperim(.; 8))
comme je n'ai pas de MATLAB sous la main, j'ai fait un petit programme en Mathematica:
m = Binarize[Import["http://imgur.com/3Zs7m.png"]] (* Get Image *)
k = Binarize[MorphologicalPerimeter[m]] (* Get Perimeter *)
p = N[2 Count[ImageData[m], Except[1], 2]/
Count[ImageData[k], Except[0], 2]] (* Calculate *)
la sortie est de 36 Px ...
le périmètre suit l'image

HTH!
Cela fait 3 ans que la question a été posée :) suivant la procédure de @nikie, voici une implémentation matlab de la largeur des traits.
clc;
clear;
close all;
I = imread('3Zs7m.png');
X = im2bw(I,0.8);
subplottight(2,2,1);
imshow(X);
Dist=bwdist(X);
subplottight(2,2,2);
imshow(Dist,[]);
RegionMax=imregionalmax(Dist);
[x, y] = find(RegionMax ~= 0);
subplottight(2,2,3);
imshow(RegionMax);
List(1:size(x))=0;
for i = 1:size(x)
List(i)=Dist(x(i),y(i));
end
fprintf('Stroke Width = %u \n',mean(List));
en supposant que la trace a une épaisseur constante, est beaucoup plus longue que large, n'est pas trop fortement courbée et n'a pas d'intersections / croisements, je suggère un algorithme de détection de bord qui détermine également la direction du bord, puis un détecteur de montée/chute avec une certaine trigonométrie et un algorithme de minimisation. Cela vous donne l'épaisseur minimale à travers une partie relativement droite de la courbe.
je suppose que l'erreur soit jusqu'à 25%.
première utilisation d'un bord détecteur qui nous donne l'information où se trouve un bord et dans quelle direction (en 45° ou PI/4 pas) il se trouve. Ceci est fait en filtrant avec 4 matrices 3x3 différentes (Exemple).
En général, je dirais qu'il suffit de scanner l'image horizontalement, mais on peut aussi scanner verticalement ou diagonalement.
En supposant un balayage ligne par ligne (horizontal), une fois que nous trouvons un bord, nous vérifions s'il s'agit d'une augmentation (passant de l'arrière-plan à la couleur de trace) ou d'une chute (à l'arrière-plan). Si l' bord de la direction est perpendiculaire à la direction de l'analyse, de l'ignorer.
Si vous trouvez une montée et une chute avec les bonnes directions et sans aucune perturbation entre les deux, mesurez la distance entre la montée et la chute. Si la direction est diagonale, multiplier par 2. Enregistrez cette mesure avec les coordonnées.
l'algorithme doit alors chercher le long d'un bord (ne peut pas trouver une ressource web sur ce moment) pour les voisins (par leur les coordonnées) des mesures. S'il y a un minimum local avec un rembourrage de peut - être 4 à 5 unités de taille de chaque côté (une valeur à jouer avec-plus grand: moins d'information, plus petit: plus de bruit), cette mesure se qualifie comme candidat. Il s'agit de s'assurer que les extrémités du sentier ou une section trop courbée ne sont pas prises en compte.
le minimum serait la mesure. Contrôle de plausibilité: Si la trace n'est pas trop embrouillé, il devrait y avoir beaucoup de valeurs que zone.
veuillez commenter s'il y a d'autres questions. : -)
Voici une réponse qui fonctionne dans n'importe quel langage de l'ordinateur sans avoir besoin de fonctions spéciales...
idée de Base: Essayez d'entrer un cercle dans les zones noires de l'image. Si vous le pouvez, essayez avec un grand cercle.
Algorithme:
- définir l'image d'arrière-plan = 0 et trace = 1
- initialiser le tableau de résultat[]
- définir minimalExpectedWidth
- ensemble w = minimalExpectedWidth
- boucle
- compteur = 0
- créer une matrice de zéros taille w x w
- dans un cercle de diamètre w dans cette matrice, mettez ceux
- calculer la superficie du cercle (=PI * w)
- parcourir tous les pixels de l'image
- optimisation: si le pixel courant est de couleur de fond - > boucle continue
- multiplier la matrice avec l'image à chaque pixel (par exemple filtrer l'image avec cette matrice) (vous pouvez le faire en utilisant la position courante x et y et un double pour boucle de 0 à w)
- prendre la somme du résultat de chaque multiplication
- si la somme est égale à la surface calculée du cercle, increment counter par un
- magasin dans le résultat[w - minimalExpectedWidth]
- incrémenter w par un
- optimisation: inclure l'algorithme de plus en bas ici
- même si compteur est plus grand zéro
maintenant le tableau de résultats contient le nombre de correspondances pour chaque largeur testée.
Graphique pour avoir un coup d'oeil.
Pour une largeur de un ce sera égale au nombre de pixels de trace de couleur. Pour une plus grande valeur de la largeur, moins de cercles s'insèrent dans la trace. Le tableau de résultat diminuera donc régulièrement jusqu'à ce qu'il y ait un chute soudaine. C'est parce que la matrice filtrante avec la zone circulaire de cette largeur ne s'adapte plus qu'aux intersections.
Juste avant la chute est la largeur de votre trace. Si la largeur n'est pas constante, la chute ne sera pas si soudaine.
Je n'ai pas de MATLAB ici pour tester et je ne suis pas sûr d'une fonction pour détecter cette chute soudaine, mais nous savons que la diminution est continue, donc je prendrais le maximum de la seconde dérivée du tableau de résultat (base zéro) comme ce
Algorithme:
- définir maximum = 0
- définir widthFound = 0
- définir minimalExpectedWidth comme ci-dessus
- définir prevvalue = result[0]
- set index = 1
- set prevfirderivative = result[1] - prevvalue
- boucle jusqu'à ce que l'index soit plus grand longueur du résultat
- firstDerivative = result[index] - prevvalue
- set secondDerivative = firstDerivative - prevFirstDerivative
- si seconddérivative > maximum ou seconddérivative < maximum * -1
- maximum = secondDerivative
- widthFound = index + minimalExpectedWidth
- prevFirstDerivative = firstDerivative
- prevvalue = result[index]
- incrémenter l'index par un
- retour widthFound
maintenant widthFound est la largeur de la trace pour laquelle (en relation à la largeur + 1) beaucoup plus d'allumettes ont été trouvées.
je sais que c'est en partie couvert dans les autres réponses, mais ma description est assez simple et vous n'avez pas à avoir appris le traitement de l'image pour le faire.
j'ai une solution intéressante:
- faire la détection de bord, pour l'extraction de pixels de bord.
- faire une simulation physique-considérer les pixels de bord comme des particules chargées positivement.
- maintenant, mettez un certain nombre de particules libres chargées positivement dans la zone de course.
- Calculez les équations de force électrique pour déterminer le mouvement de ces particules libres.
- simuler le mouvement des particules pendant un certain temps jusqu'à ce que les particules atteignent leur position équilibre. (Comme ils se repousseront des deux bords de stoke après un certain temps, ils resteront dans la ligne du milieu de stoke)
- maintenant l'épaisseur de la course / 2 serait
average distance from edge particle to nearest free particle.