Matrice De "Zigzag" Réorganisation
J'ai une matrice NXM dans MATLAB que je voudrais réorganiser de manière similaire à la façon dont JPEG réordonne ses pixels de sous-block:
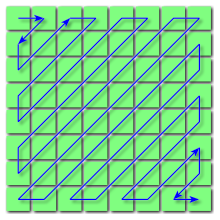 (image de Wikipedia)
(image de Wikipedia)
je voudrais que l'algorithme soit générique de sorte que je puisse passer dans une matrice 2D avec n'importe quelles dimensions. Je suis un programmeur C++ de trade et je suis très tenté d'écrire une vieille boucle pour accomplir ceci, mais je soupçonne qu'il y a une meilleure façon de le faire à MATLAB.
mise à jour: je serais plus qu'heureux avec un algorithme qui a fonctionné sur une matrice NxN et aller de là.
exemple:
1 2 3
4 5 6 --> 1 2 4 7 5 3 6 8 9
7 8 9
6 réponses
Considérez le code:
M = randi(100, [3 4]); %# input matrix
ind = reshape(1:numel(M), size(M)); %# indices of elements
ind = fliplr( spdiags( fliplr(ind) ) ); %# get the anti-diagonals
ind(:,1:2:end) = flipud( ind(:,1:2:end) ); %# reverse order of odd columns
ind(ind==0) = []; %# keep non-zero indices
M(ind) %# get elements in zigzag order
un exemple avec une matrice 4x4:
» M
M =
17 35 26 96
12 59 51 55
50 23 70 14
96 76 90 15
» M(ind)
ans =
17 35 12 50 59 26 96 51 23 96 76 70 55 14 90 15
et un exemple avec une matrice non carrée:
M =
69 9 16 100
75 23 83 8
46 92 54 45
ans =
69 9 75 46 23 16 100 83 92 54 8 45
Cette approche est assez rapide:
X = randn(500,2000); %// example input matrix
[r, c] = size(X);
M = bsxfun(@plus, (1:r).', 0:c-1);
M = M + bsxfun(@times, (1:r).'/(r+c), (-1).^M);
[~, ind] = sort(M(:));
y = X(ind).'; %'// output row vector
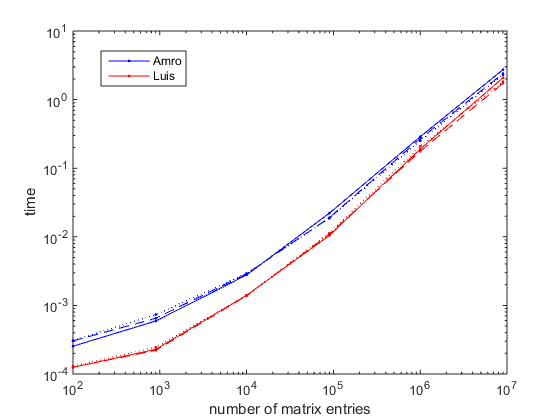
Benchmarking
le code suivant compare le temps d'exécution avec celui de l'excellente réponse D'Amro , en utilisant timeit . Il teste différentes combinaisons de taille de matrice (nombre d'entrées) et de forme de matrice (nombre de lignes par rapport au nombre de colonnes).
%// Amro's approach
function y = zigzag_Amro(M)
ind = reshape(1:numel(M), size(M));
ind = fliplr( spdiags( fliplr(ind) ) );
ind(:,1:2:end) = flipud( ind(:,1:2:end) );
ind(ind==0) = [];
y = M(ind);
%// Luis' approach
function y = zigzag_Luis(X)
[r, c] = size(X);
M = bsxfun(@plus, (1:r).', 0:c-1);
M = M + bsxfun(@times, (1:r).'/(r+c), (-1).^M);
[~, ind] = sort(M(:));
y = X(ind).';
%// Benchmarking code:
S = [10 30 100 300 1000 3000]; %// reference to generate matrix size
f = [1 1]; %// number of cols is S*f(1); number of rows is S*f(2)
%// f = [0.5 2]; %// plotted with '--'
%// f = [2 0.5]; %// plotted with ':'
t_Amro = NaN(size(S));
t_Luis = NaN(size(S));
for n = 1:numel(S)
X = rand(f(1)*S(n), f(2)*S(n));
f_Amro = @() zigzag_Amro(X);
f_Luis = @() zigzag_Luis(X);
t_Amro(n) = timeit(f_Amro);
t_Luis(n) = timeit(f_Luis);
end
loglog(S.^2*prod(f), t_Amro, '.b-');
hold on
loglog(S.^2*prod(f), t_Luis, '.r-');
xlabel('number of matrix entries')
ylabel('time')
la figure ci-dessous a été obtenue avec Matlab R2014 B sur Windows 7 64 bits. Les résultats de R2010b sont très similaires. On voit que la nouvelle approche réduit le temps de fonctionnement d'un facteur compris entre 2,5 (pour les petites matrices) et 1,4 (pour les grandes matrices). Les résultats semblent être presque insensibles à la forme de la matrice, compte tenu du nombre total d'entrées.
Voici une solution sans boucle zig_zag.m . Il semble laid, mais il fonctionne!:
function [M,index] = zig_zag(M)
[r,c] = size(M);
checker = rem(hankel(1:r,r-1+(1:c)),2);
[rEven,cEven] = find(checker);
[cOdd,rOdd] = find(~checker.'); %'#
rTotal = [rEven; rOdd];
cTotal = [cEven; cOdd];
[junk,sortIndex] = sort(rTotal+cTotal);
rSort = rTotal(sortIndex);
cSort = cTotal(sortIndex);
index = sub2ind([r c],rSort,cSort);
M = M(index);
end
et une matrice d'essai:
>> M = [magic(4) zeros(4,1)];
M =
16 2 3 13 0
5 11 10 8 0
9 7 6 12 0
4 14 15 1 0
>> newM = zig_zag(M) %# Zig-zag sampled elements
newM =
16
2
5
9
11
3
13
10
7
4
14
6
8
0
0
12
15
1
0
0
voici un moyen de le faire. Fondamentalement, votre tableau est une matrice de hankel plus vecteurs de 1:m, où m est le nombre d'éléments dans chaque diagonale. Peut-être que quelqu'un d'autre a une bonne idée sur la façon de créer les tableaux diagonaux qui doivent être ajoutés au tableau Hankel retourné sans boucle.
je pense que cela devrait être généralisable à un tableau non carré.
% for a 3x3 array
n=3;
numElementsPerDiagonal = [1:n,n-1:-1:1];
hadaRC = cumsum([0,numElementsPerDiagonal(1:end-1)]);
array2add = fliplr(hankel(hadaRC(1:n),hadaRC(end-n+1:n)));
% loop through the hankel array and add numbers counting either up or down
% if they are even or odd
for d = 1:(2*n-1)
if floor(d/2)==d/2
% even, count down
array2add = array2add + diag(1:numElementsPerDiagonal(d),d-n);
else
% odd, count up
array2add = array2add + diag(numElementsPerDiagonal(d):-1:1,d-n);
end
end
% now flip to get the result
indexMatrix = fliplr(array2add)
result =
1 2 6
3 5 7
4 8 9
ensuite, il suffit d'appeler reshape(image(indexMatrix),[],1) pour obtenir le vecteur de réorganisé élément.
MODIFIER
Ok, de votre commentaire il semble que vous devez utiliser sort comme Marc suggéré.
indexMatrixT = indexMatrix'; % ' SO formatting
[dummy,sortedIdx] = sort(indexMatrixT(:));
sortedIdx =
1 2 4 7 5 3 6 8 9
notez que vous devez d'abord transposer votre matrice d'entrée avant d'indexer, parce que Matlab compte d'abord vers le bas, puis vers la droite.
en supposant que X soit la matrice 2D d'entrée et que soit square ou landscape-shaped , cela semble être assez efficace -
[m,n] = size(X);
nlim = m*n;
n = n+mod(n-m,2);
mask = bsxfun(@le,[1:m]',[n:-1:1]);
start_vec = m:m-1:m*(m-1)+1;
a = bsxfun(@plus,start_vec',[0:n-1]*m);
offset_startcol = 2- mod(m+1,2);
[~,idx] = min(mask,[],1);
idx = idx - 1;
idx(idx==0) = m;
end_ind = a([0:n-1]*m + idx);
offsets = a(1,offset_startcol:2:end) + end_ind(offset_startcol:2:end);
a(:,offset_startcol:2:end) = bsxfun(@minus,offsets,a(:,offset_startcol:2:end));
out = a(mask);
out2 = m*n+1 - out(end:-1:1+m*(n-m+1));
result = X([out2 ; out(out<=nlim)]);
Rapide d'exécution des tests contre Luis approche du -
Datasize: 500 x 2000
------------------------------------- With Proposed Approach
Elapsed time is 0.037145 seconds.
------------------------------------- With Luis Approach
Elapsed time is 0.045900 seconds.
Datasize: 5000 x 20000
------------------------------------- With Proposed Approach
Elapsed time is 3.947325 seconds.
------------------------------------- With Luis Approach
Elapsed time is 6.370463 seconds.
supposons pour un moment que vous avez une matrice 2-D qui est la même taille que votre image spécifiant l'index correct. Appelez ce tableau idx; alors les commandes matlab pour réordonner votre image seraient
[~,I] = sort (idx(:)); %sort the 1D indices of the image into ascending order according to idx
reorderedim = im(I);
Je ne vois pas de solution évidente pour générer idx sans utiliser pour les boucles ou la récursion, mais je vais réfléchir encore un peu.