matplotlib (longueur unitaire égale): avec un rapport d'aspect "égal", l'axe z n'est pas égal à x-et y-
quand je mets en place un rapport d'aspect égal pour un graphe 3d, l'axe z ne change pas en "égal". Ainsi, ceci:
fig = pylab.figure()
mesFig = fig.gca(projection='3d', adjustable='box')
mesFig.axis('equal')
mesFig.plot(xC, yC, zC, 'r.')
mesFig.plot(xO, yO, zO, 'b.')
pyplot.show()
me donne le suivant:
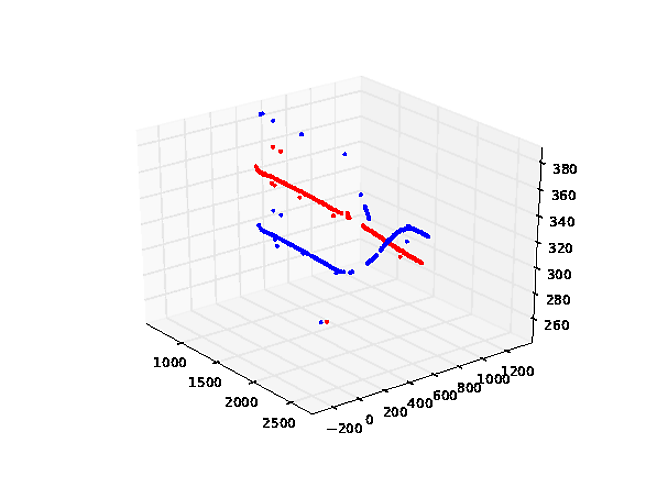
où, de toute évidence, la longueur unitaire de l'axe z n'est pas égale aux unités x et Y.
comment rendre la longueur unitaire des trois axes égale? Toutes les solutions que j'ai pu trouver n'ont pas fonctionné. Remercier.
5 réponses
je crois que matplotlib n'a pas encore positionné correctement l'axe égal en 3D... Mais j'ai trouvé un truc il y a quelques temps (Je ne me souviens pas où) que j'ai adapté en l'utilisant. Le concept est de créer une fausse boîte de limite cubique autour de vos données. Vous pouvez le tester avec le code suivant:
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect('equal')
X = np.random.rand(100)*10+5
Y = np.random.rand(100)*5+2.5
Z = np.random.rand(100)*50+25
scat = ax.scatter(X, Y, Z)
# Create cubic bounding box to simulate equal aspect ratio
max_range = np.array([X.max()-X.min(), Y.max()-Y.min(), Z.max()-Z.min()]).max()
Xb = 0.5*max_range*np.mgrid[-1:2:2,-1:2:2,-1:2:2][0].flatten() + 0.5*(X.max()+X.min())
Yb = 0.5*max_range*np.mgrid[-1:2:2,-1:2:2,-1:2:2][1].flatten() + 0.5*(Y.max()+Y.min())
Zb = 0.5*max_range*np.mgrid[-1:2:2,-1:2:2,-1:2:2][2].flatten() + 0.5*(Z.max()+Z.min())
# Comment or uncomment following both lines to test the fake bounding box:
for xb, yb, zb in zip(Xb, Yb, Zb):
ax.plot([xb], [yb], [zb], 'w')
plt.grid()
plt.show()
z données sont environ un ordre de grandeur plus grand que x et y, mais même avec l'option d'axe égal, matplotlib autoscale Z axe:
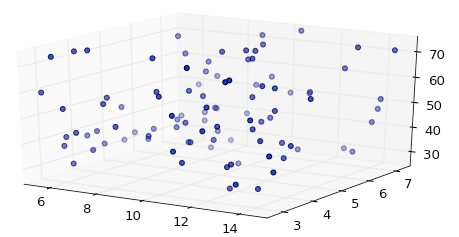
mais si vous ajoutez la boîte de limite, vous obtenez une échelle correcte:
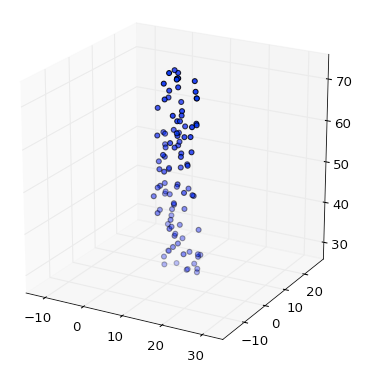
j'ai simplifié la solution de Remy F en utilisant les set_x/y/zlim fonctions .
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect('equal')
X = np.random.rand(100)*10+5
Y = np.random.rand(100)*5+2.5
Z = np.random.rand(100)*50+25
scat = ax.scatter(X, Y, Z)
max_range = np.array([X.max()-X.min(), Y.max()-Y.min(), Z.max()-Z.min()]).max() / 2.0
mid_x = (X.max()+X.min()) * 0.5
mid_y = (Y.max()+Y.min()) * 0.5
mid_z = (Z.max()+Z.min()) * 0.5
ax.set_xlim(mid_x - max_range, mid_x + max_range)
ax.set_ylim(mid_y - max_range, mid_y + max_range)
ax.set_zlim(mid_z - max_range, mid_z + max_range)
plt.show()
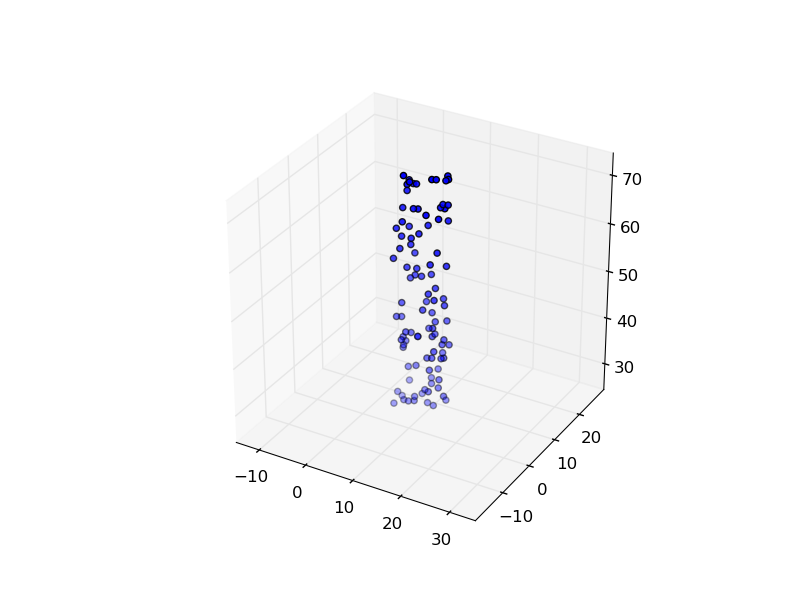
j'aime les solutions ci-dessus, mais ils ont l'inconvénient que vous devez garder la trace des gammes et des moyens sur toutes vos données. Cela pourrait être compliqué si vous avez plusieurs ensembles de données qui seront tracés ensemble. Pour résoudre ce problème, j'ai fait usage de la hache.utilisez les méthodes get_ [xyz]lim3d() et mettez le tout dans une fonction autonome qui peut être appelée juste une fois avant d'appeler plt.montrer.)( Voici la nouvelle version:
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
def set_axes_equal(ax):
'''Make axes of 3D plot have equal scale so that spheres appear as spheres,
cubes as cubes, etc.. This is one possible solution to Matplotlib's
ax.set_aspect('equal') and ax.axis('equal') not working for 3D.
Input
ax: a matplotlib axis, e.g., as output from plt.gca().
'''
x_limits = ax.get_xlim3d()
y_limits = ax.get_ylim3d()
z_limits = ax.get_zlim3d()
x_range = abs(x_limits[1] - x_limits[0])
x_middle = np.mean(x_limits)
y_range = abs(y_limits[1] - y_limits[0])
y_middle = np.mean(y_limits)
z_range = abs(z_limits[1] - z_limits[0])
z_middle = np.mean(z_limits)
# The plot bounding box is a sphere in the sense of the infinity
# norm, hence I call half the max range the plot radius.
plot_radius = 0.5*max([x_range, y_range, z_range])
ax.set_xlim3d([x_middle - plot_radius, x_middle + plot_radius])
ax.set_ylim3d([y_middle - plot_radius, y_middle + plot_radius])
ax.set_zlim3d([z_middle - plot_radius, z_middle + plot_radius])
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect('equal')
X = np.random.rand(100)*10+5
Y = np.random.rand(100)*5+2.5
Z = np.random.rand(100)*50+25
scat = ax.scatter(X, Y, Z)
set_axes_equal(ax)
plt.show()
EDIT: user2525140 du code devrait fonctionner parfaitement bien, même si cette réponse soi-disant tenté de fixer un non-existant erreur. La réponse ci-dessous est juste un double (alternative) implémentation:
def set_aspect_equal_3d(ax):
"""Fix equal aspect bug for 3D plots."""
xlim = ax.get_xlim3d()
ylim = ax.get_ylim3d()
zlim = ax.get_zlim3d()
from numpy import mean
xmean = mean(xlim)
ymean = mean(ylim)
zmean = mean(zlim)
plot_radius = max([abs(lim - mean_)
for lims, mean_ in ((xlim, xmean),
(ylim, ymean),
(zlim, zmean))
for lim in lims])
ax.set_xlim3d([xmean - plot_radius, xmean + plot_radius])
ax.set_ylim3d([ymean - plot_radius, ymean + plot_radius])
ax.set_zlim3d([zmean - plot_radius, zmean + plot_radius])
adapté de la réponse de @karlo pour rendre les choses encore plus propres:
def set_axes_radius(ax, origin, radius):
ax.set_xlim3d([origin[0] - radius, origin[0] + radius])
ax.set_ylim3d([origin[1] - radius, origin[1] + radius])
ax.set_zlim3d([origin[2] - radius, origin[2] + radius])
def set_axes_equal(ax):
'''Make axes of 3D plot have equal scale so that spheres appear as spheres,
cubes as cubes, etc.. This is one possible solution to Matplotlib's
ax.set_aspect('equal') and ax.axis('equal') not working for 3D.
Input
ax: a matplotlib axis, e.g., as output from plt.gca().
'''
limits = np.array([
ax.get_xlim3d(),
ax.get_ylim3d(),
ax.get_zlim3d(),
])
origin = np.mean(limits, axis=1)
radius = 0.5 * np.max(np.abs(limits[:, 1] - limits[:, 0]))
set_axes_radius(ax, origin, radius)
Utilisation:
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect('equal') # important!
# ...draw here...
set_axes_equal(ax) # important!
plt.show()