Analyse comparative des performances de MATLAB
:
Ce poste est à propos de tester les performances des solutions pour le problème suivant:
une rangée de cellules de
Sles chaînes formatées en Nombres séparés par des underscores sont données, par exemple:
list_of_words = repmat({'02_04_04_52_23_14_54_672_0'},10,1);Est garanti pour toutes les chaînes que:
- ils ne contiennent que des chiffres et des caractères de soulignement;
- le nombre de traits de soulignement est le même;
- il n'y a pas deux soulignements consécutifs.
écrire le code MATLAB qui convertirait le tableau de cellules de chaînes en une matrice numérique
S×Mdouble (valeurs 1000 fois plus petites), oùSest le nombre de chaînes et deMest le nombre de nombres dans une chaîne.
un problème très similaire était affiché sur StackOverflow, avec plusieurs solutions proposées. Le but initial était d'améliorer les performances de vitesse.
le code:
deux des solutions, conçues pour la vitesse, semblent avoir des performances très variables d'une installation MATLAB à l'autre, ou même d'une exécution à l'autre. En outre, ils ont vraiment différents styles d'implémentation.
Dans le coin noir vous trouverez une solution qui va bien contre MATLAB plus dogmes sacrés: eval est mauvais, et les boucles doivent être évitées à tout prix. Cependant, le code essaie d'optimiser la vitesse en évitant les attributions de mémoire répétées, en utilisant les moyens rapides de convertir les chaînes en nombres, et en faisant des opérations en place:
%'eval_and_loops_solution.m'
function array_of_numbers = eval_and_loops_solution(list_of_words)
n_numbers = 1 + sum(list_of_words{1}=='_');
n_words = numel(list_of_words);
array_of_numbers = zeros(n_numbers, n_words);
for k = 1:n_words
temp = ['[', list_of_words{k}, ']'];
temp(temp=='_') = ';';
array_of_numbers(:,k) = eval(temp);
end;
%'this is a waste of memory, but is kind of required'
array_of_numbers = transpose(array_of_numbers / 1000);
end
Remarque: La solution d'origine retourné le résultat sous la forme M×Sdouble array. Le code a été adapté pour S×M; toutefois, cette adaptation consomme deux fois plus de mémoire. Et oui, je a écrit cette solution.
En clair coin vous trouverez une solution fidèle à MATLAB spirit, qui évite d'utiliser des boucles et eval, en faveur d'un simple sscanf lire les chaînes de caractères (ce qui est une façon habile d'éviter la surcharge de l'appel de la fonction S fois):
%'single_sscanf_solution.m'
function array_of_numbers = single_sscanf_solution(list_of_words)
N = 1 + sum(list_of_words{1}=='_'); %'hard-coded in the original'
lens = cellfun(@numel,list_of_words);
tlens = sum(lens);
idx(1,tlens)=0;
idx(cumsum(lens(1:end-1))+1)=1;
idx2 = (1:tlens) + cumsum(idx);
one_str(1:max(idx2)+1)='_';
one_str(idx2) = [list_of_words{:}];
delim = repmat('%d_',1,N*numel(lens));
array_of_numbers = reshape(sscanf(one_str, delim),N,[])'./1000;
end
Remarque: Cette solution appartient à @Divakar.
L'arbitre est constitué de deux fonctions: une qui génère des cas de test, et une qui fait le timig.
le générateur de cas d'essai regroupe dans un tableau de cellules des chaînes délimitées par un trait de soulignement sur 10 entiers aléatoires entre 1 et 9999 (pour des raisons de simplicité); cependant, une implémentation ne devrait supposer que les nombres sont positifs ou zéro, et le nombre devrait correspondre à un double:
%'referee_test_case.m'
function list_of_words = referee_test_case(n_words)
NUM_PER_WORD = 10;
NUM_MAX = 9999;
word_format = [repmat('%d_', 1, NUM_PER_WORD-1), '%d'];
list_of_words = cell(n_words,1);
fprintf('Generating %d-words test case...n', n_words);
for k = 1:n_words
list_of_words{k} = sprintf(word_format, randi(NUM_MAX, [1, NUM_PER_WORD]));
end;
end
la fonction timing prend comme arguments un cas de test et un nombre arbitraire de fonction processing poignées; il est mis en œuvre, telles que les erreurs dans une fonction ne devrait pas gêner l'exécution des autres. Il utilise timeit comme recommandé par @Divakar et @LuisMendo; pour ceux qui n'ont pas cette fonction dans leur installation MATLAB par défaut, il peut être téléchargé depuis MATLAB Central / échange de fichiers:
%'referee_timing.m'
function referee_timing(test_case, varargin)
%' Specify the test case as a cell array of strings, then the function '
%' handles that will process the test case. '
%' '
%' The function uses timeit() to evaluate the performance of different '
%' processing handles; if your MATLAB installation does not have it '
%' natively, download the available version from File Exchange: '
%' '
%' http://www.mathworks.com/matlabcentral/fileexchange/18798-timeit-benchmarking-function '
fprintf('Timing %d-words test case...n', numel(test_case));
for k = 1:numel(varargin)
try
t = timeit(@() varargin{k}(test_case));
fprintf(' %s: %f[s]n', func2str(varargin{k}), t);
catch ME
fprintf(' %s: Error - %sn', func2str(varargin{k}), ME.message);
end;
end;
end
Le problème:
comme nous l'avons dit plus haut, les résultats semblent varier d'une installation de MATLAB à l'autre, et même d'une exécution à l'autre. Le problème que j'ai la proposition est triple:
- sur votre installation MATLAB spécifique (version + OS + HW), Quel est le rendement des deux solutions par rapport à L'autre?
- Est-il possible d'améliorer une solution ou l'autre dans une assez grande manière?
- Existe-t-il des solutions MATLAB-natives encore plus rapides (par exemple sans MEX ou boîtes à outils spéciales) basées sur des idées/fonctions complètement différentes?
pour le point 1. (benchmarking), veuillez créer dans votre chemin MATLAB quatre fichiers de fonctions eval_and_loops_solution.m,single_sscanf_solution.m,referee_test_case.m,referee_timig.m et d'autres fonctions que vous pouvez tester (par exemple, les implémentations proposées par des réponses). Utilisez - les pour plusieurs nombres de mots, par exemple comme ce script:
%'test.m'
clc;
feature accel on; %'tune for speed'
%'low memory stress'
referee_timing( ...
referee_test_case(10^4), ...
@eval_and_loops_solution, ...
@single_sscanf_solution ... %'add here other functions'
);
%'medium memory stress'
referee_timing( ...
referee_test_case(10^5), ...
@eval_and_loops_solution, ...
@single_sscanf_solution ... %'add here other functions'
);
%'high memory stress'
referee_timing( ...
referee_test_case(10^6), ...
@eval_and_loops_solution, ...
@single_sscanf_solution ... %'add here other functions'
);
lors de la publication des résultats, Veuillez spécifier votre version MATLAB, le système D'exploitation, la taille de la RAM et le modèle CPU. s'il vous plaît soyez conscient que ces tests peuvent prendre un certain temps pour un grand nombre de mots! cependant, l'exécution de ce script ne pas modifier le contenu de votre espace de travail courant.
pour les points 2. ou 3. vous pouvez poster un code qui utilise les mêmes conventions in/out que eval_and_loops_solution.m et single_sscanf_solution.m, ainsi que l'analyse comparative à l'appui de la réclamation.
Les bienfaits:
je voterai chaque réponse de benchmarking, et j'encourage tout le monde à le faire. Est le moins que l'on puisse faire pour les gens qui contribuent avec leurs compétences, le temps et le pouvoir de traitement.
a +500 Bonus bounty ira à l'auteur du code le plus rapide, que ce soit l'un des deux proposés, ou un troisième nouveau qui les surpasse. J'espère vraiment que cela correspondra à l'accord général. Le bonus sera donné dans un mois semaine à partir de la date d'affichage originale.
9 réponses
approche #1
cumsum. Le second, basé surbsxfun nous donne la sortie numérique désirée dans le format désiré.
Le code devrait ressembler à quelque chose comme cela -
function out = solution_cumsum_bsxfun(list_of_words)
N = 1 + sum(list_of_words{1}=='_'); %// Number of "words" per cell
lens = cellfun('length',list_of_words); %// No. of chars [lengths] in each cell
tlens = sum(lens); %// Total number of characters [total of lengths]
cumlens = cumsum(lens); %// Cumulative lengths
%// Create an array of ones and zeros.
%// The length of this array would be equal to sum of characters in all cells.
%// The ones would be at the positions where new cells start, zeros otherwise
startpos_newcell(1,tlens)=0;
startpos_newcell(cumlens(1:end-1)+1)=1;
%// Calculate new positions for all characters in the cell array with
%// places/positions left between two cells for putting underscores
newpos = (1:tlens) + cumsum(startpos_newcell);
%// Create one long string that has all the characters from the cell arary
%// with underscores separating cells
one_str(newpos) = [list_of_words{:}];
one_str(cumlens + [1:numel(cumlens)]') = '_'; %//'#
pos_us = find(one_str=='_'); %// positions of underscores
wordend_idx = pos_us - [1:numel(pos_us)]; %// word end indices
wordlens = [wordend_idx(1) diff(wordend_idx)]; %// word lengths
max_wordlens = max(wordlens); %// maximum word length
%// Create mask where digit characters are to be placed
mask = bsxfun(@ge,[1:max_wordlens]',[max_wordlens+1-wordlens]); %//'#
%// Create a numeric array with columns for each word and each row holding a digit.
%// The most significant digits to least significant going from top to bottom
num1(max_wordlens,size(mask,2)) = 0;
num1(mask) = one_str(one_str~='_') - 48;
%// Finally get the desired output converting each column to a single
%// number, reshaping to desired size and scaling down by a factor of 1000
out = reshape(10.^(max_wordlens-4:-1:-3)*num1,N,[]).'; %//'#
return;
Approche #2
c'est une légère variation de l'approche #1 en ce qu'elle fait le travail de la première partie avec sprintf. Maintenant, l'idée m'est venue après avoir vu en action dans
la solution de@chappjc. J'apprécie qu'il me laisse l'utiliser dans cette version modifiée.
Voici le code
function out = solution_sprintf_bsxfun(list_of_words)
N = 1 + sum(list_of_words{1}=='_'); %// Number of "words" per cell
%// Create one long string that has all the characters from the cell arary
%// with underscores separating cells
one_str = sprintf('%s_',list_of_words{:});
pos_us = find(one_str=='_'); %// positions of underscores
wordend_idx = pos_us - [1:numel(pos_us)]; %// word end indices
wordlens = [wordend_idx(1) diff(wordend_idx)]; %// word lengths
max_wordlens = max(wordlens); %// maximum word length
%// Create mask where digit characters are to be placed
mask = bsxfun(@ge,[1:max_wordlens]',[max_wordlens+1-wordlens]); %//'#
%// Create a numeric array with columns for each word and each row holding a digit.
%// The most significant digits to least significant going from top to bottom
num1(max_wordlens,size(mask,2)) = 0;
num1(mask) = one_str(one_str~='_') - 48;
%// Finally get the desired output converting each column to a single
%// number, reshaping to desired size and scaling down by a factor of 1000
out = reshape(10.^(max_wordlens-4:-1:-3)*num1,N,[]).'; %//'#
return;
approche #3
C'est une approche tout à fait nouvelle basée sur getByteStreamFromArray -
function out = solution_bytstrm_bsxfun(list_of_words)
allchars = [list_of_words{:}];
digits_array = getByteStreamFromArray(allchars);
%// At my 32-bit system getByteStreamFromArray gets the significant digits
%// from index 65 onwards. Thus, we need to crop/index it accordingly
digits_array = digits_array(65:65+numel(allchars)-1) - 48;
% --------------------------------------------------------------------
N = 1 + sum(list_of_words{1}=='_'); %// Number of "words" per cell
lens = cellfun('length',list_of_words); %// No. of chars [lengths] in each cell
cumlens = cumsum(lens)'; %//'# Cumulative lengths
% ----------------------------------------------------------
pos_us = find(digits_array==47);
starts = [[1 cumlens(1:end-1)+1];reshape(pos_us+1,N-1,[])];
ends = [reshape(pos_us-1,N-1,[]) ; cumlens];
gaps = ends(:) - starts(:) + 1;
maxg = max(gaps);
mask1 = bsxfun(@lt,maxg-gaps',[1:maxg]');
num_array(maxg,numel(lens)*N)=0;
num_array(mask1) = digits_array(digits_array~=47);
out = reshape(10.^(maxg-4:-1:-3)*num_array,N,[]).';
return;
GPU les versions des approches ci-dessus sont décrites ci-après.
approche #4
function out = soln_sprintf_bsxfun_gpu(list_of_words)
N = 1 + sum(list_of_words{1}=='_'); %// Number of "words" per cell
%// Create one long string that has all the characters from the cell arary
%// with underscores separating cells. Now this one uses sprintf as
%// firstly proposed in @chappjc's solution and he has agreed to let me use
%// it, so appreciating his help on this.
digits_array = gpuArray(single(sprintf('%s_',list_of_words{:})));
digits_array = digits_array - 48;
mask_us = digits_array==47; %// mask of underscores
pos_us = find(mask_us);
wordend_idx = pos_us - gpuArray.colon(1,numel(pos_us)); %// word end indices
wordlens = [wordend_idx(1) diff(wordend_idx)]; %// word lengths
max_wordlens = max(wordlens); %// maximum word length
%// Create a numeric array with columns for each word and each row holding a digit.
%// The most significant digits to least significant going from top to bottom
num1 = single(zeros(max_wordlens,numel(pos_us),'gpuArray')); %//'
num1(bsxfun(@ge,gpuArray.colon(1,max_wordlens)',...
max_wordlens+1-single(wordlens))) = digits_array(~mask_us); %//'
%// Finally get the desired output converting each column to a single
%// number, reshaping to desired size and scaling down by a factor of 1000
outg = reshape(10.^(max_wordlens-4:-1:-3)*num1,N,[]).'; %//'#
out = gather(outg);
return;
approche # 5
function out = soln_bytstrm_bsxfun_gpu(list_of_words)
us_ascii_num = 95;
allchars = [list_of_words{:}];
%// At my 32-bit system getByteStreamFromArray gets the significant digits
%// from index 65 onwards. Thus, we need to crop/index it accordingly
alldigits = getByteStreamFromArray(allchars);
digits_array1 = gpuArray(alldigits(65:65+numel(allchars)-1));
% --------------------------------------------------------------------
lens = cellfun('length',list_of_words); %// No. of chars [lengths] in each cell
N = sum(digits_array1(1:lens(1))==us_ascii_num)+1; %// Number of "words" per cell
lens = gpuArray(lens);
cumlens = cumsum(lens)'; %//'# Cumulative lengths
% ----------------------------------------------------------
mask_us = digits_array1==us_ascii_num; %// mask of underscores
pos_us = find(mask_us);
starts = [[1 cumlens(1:end-1)+1];reshape(pos_us+1,N-1,[])];
ends = [reshape(pos_us-1,N-1,[]) ; cumlens];
gaps = ends(:) - starts(:) + 1;
maxg = max(gaps);
mask1 = bsxfun(@lt,maxg-gaps',[1:maxg]');
num_array = zeros(maxg,numel(lens)*N,'gpuArray'); %//'
num_array(mask1) = digits_array1(~mask_us)-48;
out = reshape(10.^(maxg-4:-1:-3)*num_array,N,[]).'; %//'
out = gather(out);
return;
voici un tas d'implémentations pour vous de benchmark (toutes purement MATLAB). Certains d'entre eux empruntent des idées aux autres solutions.
function M = func_eval_strjoin(C)
M = eval(['[' strjoin(strrep(C,'_',' ').',';') ']']);
end
function M = func_eval_sprintf(C)
C = strrep(C,'_',' ');
M = eval(['[' sprintf('%s;',C{:}) ']']);
end
function M = func_eval_cellfun(C)
M = cell2mat(cellfun(@eval, strcat('[',strrep(C,'_',' '),']'), 'Uniform',false));
end
function M = func_eval_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
M(i,:) = eval(['[' strrep(C{i},'_',' ') ']']);
end
end
function M = func_str2num_strjoin(C)
M = reshape(str2num(strjoin(strrep(C.','_',' '))), [], numel(C)).';
end
function M = func_str2num_sprintf(C)
C = strrep(C,'_',' ');
M = reshape(str2num(sprintf('%s ',C{:})), [], numel(C)).';
end
function M = func_str2num_cellfun(C)
M = cell2mat(cellfun(@str2num, strrep(C, '_', ' '), 'Uniform',false));
end
function M = func_str2num_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
M(i,:) = str2num(strrep(C{i}, '_', ' '));
end
end
function M = func_sscanf_strjoin(C)
M = reshape(sscanf(strjoin(C', '_'), '%f_'), [], numel(C)).';
end
function M = func_sscanf_sprintf(C)
M = reshape(sscanf(sprintf('%s_',C{:}),'%f_'), [], numel(C)).';
end
function M = func_sscanf_cellfun(C)
M = cell2mat(cellfun(@(c) sscanf(c, '%f_'), C, 'Uniform',false).').';
end
function M = func_sscanf_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
M(i,:) = sscanf(C{i}, '%f_');
end
end
function M = func_textscan_strjoin(C)
M = textscan(strjoin(C', '_'), '%.0f', 'Delimiter','_');
M = reshape(M{1}, [], numel(C)).';
end
function M = func_textscan_sprintf(C)
M = textscan(sprintf('%s_',C{:}),'%.0f', 'Delimiter','_');
M = reshape(M{1}, [], numel(C)).';
end
function M = func_textscan_cellfun(C)
M = cell2mat(cellfun(@(str) textscan(str, '%.0f', 'Delimiter','_'), C).').';
end
function M = func_textscan_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
x = textscan(C{i}, '%.0f', 'Delimiter','_');
M(i,:) = x{1};
end
end
function M = func_str2double_strsplit_strjoin(C)
M = reshape(str2double(strsplit(strjoin(C','_'),'_')), [], numel(C)).';
end
function M = func_str2double_strsplit_sprintf(C)
M = strsplit(sprintf('%s_',C{:}), '_');
M = reshape(str2double(M(1:end-1)), [], numel(C)).';
end
function M = func_str2double_strsplit(C)
M = cellfun(@(c) strsplit(c,'_'), C, 'Uniform',false);
M = str2double(cat(1,M{:}));
end
function M = func_str2double_strsplit_cellfun(C)
M = cell2mat(cellfun(@(c) str2double(strsplit(c,'_')), C, 'Uniform',false));
end
function M = func_str2double_strsplit_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
M(i,:) = str2double(strsplit(C{i},'_'));
end
end
function M = func_str2double_regex_split_strjoin(C)
M = reshape(str2double(regexp(strjoin(C.','_'), '_', 'split')), [], numel(C)).';
end
function M = func_str2double_regex_split_sprintf(C)
M = regexp(sprintf('%s_',C{:}), '_', 'split');
M = reshape(str2double(M(1:end-1)), [], numel(C)).';
end
function M = func_str2double_regex_split(C)
M = regexp(C, '_', 'split');
M = reshape(str2double([M{:}]), [], numel(C)).';
end
function M = func_str2double_regex_split_cellfun(C)
M = cell2mat(cellfun(@str2double, regexp(C, '_', 'split'), 'Uniform',false));
end
function M = func_str2double_regex_split_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
M(i,:) = str2double(regexp(C{i}, '_', 'split'));
end
end
function M = func_str2double_regex_tokens_strjoin_1(C)
M = reshape(cellfun(@str2double, regexp(strjoin(C.','_'), '(\d+)', 'tokens')), [], numel(C)).';
end
function M = func_str2double_regex_tokens_strjoin_2(C)
M = regexp(strjoin(C.','_'), '(\d+)', 'tokens');
M = reshape(str2double([M{:}]), [], numel(C)).';
end
function M = func_str2double_regex_tokens_sprintf_1(C)
M = reshape(cellfun(@str2double, regexp(sprintf('%s_',C{:}), '(\d+)', 'tokens')), [], numel(C)).';
end
function M = func_str2double_regex_tokens_sprintf_2(C)
M = regexp(sprintf('%s_',C{:}), '(\d+)', 'tokens');
M = reshape(str2double([M{:}]), [], numel(C)).';
end
function M = func_str2double_regex_tokens(C)
M = regexp(C, '(\d+)', 'tokens');
M = cat(1,M{:});
M = reshape(str2double([M{:}]), size(M));
end
function M = func_str2double_regex_tokens_cellfun(C)
M = regexp(C, '(\d+)', 'tokens');
M = cellfun(@str2double, cat(1,M{:}));
end
function M = func_str2double_regex_tokens_loop(C)
M = zeros(numel(C),nnz(C{1}=='_')+1);
for i=1:numel(C)
x = regexp(C{i}, '(\d+)', 'tokens');
M(i,:) = str2double([x{:}]);
end
end
la plupart des méthodes sont des variantes de la même idée, mais avec des implémentations légèrement différentes (E. g: utiliser explicit for-loop vs. cellfun, en utilisant strjoin vs. sprintf pour joindre un tableau de cellules de chaînes en une chaîne, etc..).
Permettez-moi de le décomposer un peu plus:
il y a
evalbasée sur des solutions. Nous appliquerevaldans une boucle, ou nous faisons un seul appel après avoir aplati les cordes en une seule.de même, il existe des solutions basées sur l'appel
str2num(après remplacement des soulignements par des espaces). Il est intéressant de noter questr2numappelle lui-mêmeevalen interne.il y a aussi le
sscanfettextscandes solutions. Comme avant, nous les utiliser dans une boucle, ou appelé sur une longue chaîne.un autre ensemble de solutions est basé sur l'appel
str2doubleaprès avoir séparé les chaînes par le délimiteur de soulignement. Encore une fois, il existe d'autres façons de diviser les chaînes (en utilisantregexavec l'option" split", ou en utilisant lestrsplitfonction).enfin, il y a un ensemble de solutions basées sur l'expression régulière correspondre.
EDIT:
j'ai créé un ensemble de fonctions pour comparer les différentes implémentations ( GitHub Gist). Voici les pré-emballés fichiers avec toutes les solutions publié jusqu'à présent. J'ai inclus les fonctions MEX compilées (pour Windows 64 bits), ainsi que les dépendances de DLL MinGW-w64.
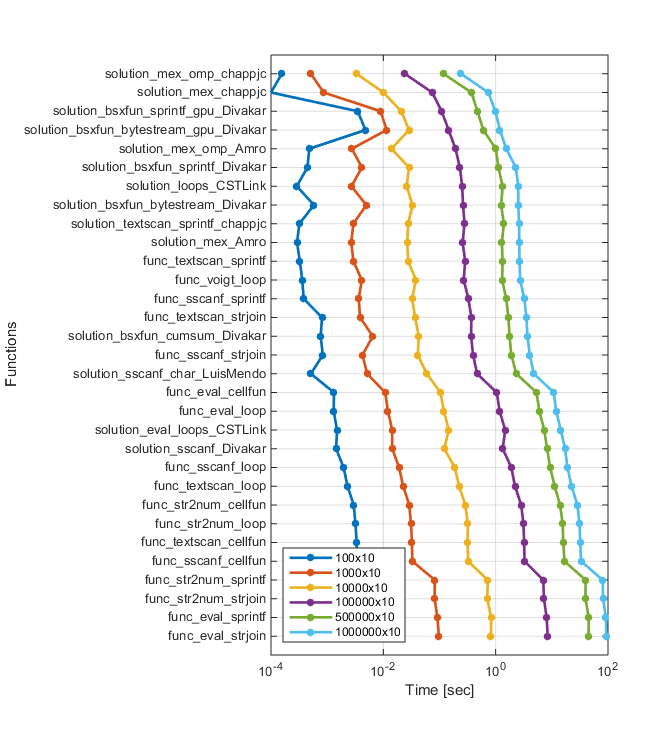
Voici les résultats de l'exécution sur ma machine (Ordinateur Portable avec quad-core Intel Core i7 CPU, 8GB, Win8.(1), MATLAB R2014 a). J'ai testé les tailles suivantes: 10x10, 100x10, 1000x10, et 10000x10. Comme vous pouvez le voir, les solutions MEX fonctionnent mieux lorsque vous augmentez la taille des données...
EDIT#2:
comme demandé, j'ai mis à jour mes résultats de tests avec les dernières solutions; j'ai ajouté les versions modifiées du fichier MEX par @chappjc, et les versions GPU par @Divakar. Voici le mise à jour des archives de fichiers.
je suis en utilisant la même machine que avant. J'ai augmenté la taille du réseau cellulaire à 1e5. Mon appareil GPU est décent pour un ordinateur portable:
>> gpuDevice
ans =
CUDADevice with properties:
Name: 'GeForce GT 630M'
Index: 1
ComputeCapability: '2.1'
SupportsDouble: 1
DriverVersion: 5.5000
ToolkitVersion: 5.5000
MaxThreadsPerBlock: 1024
MaxShmemPerBlock: 49152
MaxThreadBlockSize: [1024 1024 64]
MaxGridSize: [65535 65535 65535]
SIMDWidth: 32
TotalMemory: 2.1475e+09
FreeMemory: 2.0453e+09
MultiprocessorCount: 2
ClockRateKHz: 950000
ComputeMode: 'Default'
GPUOverlapsTransfers: 1
KernelExecutionTimeout: 1
CanMapHostMemory: 1
DeviceSupported: 1
DeviceSelected: 1
Voici les derniers résultats:
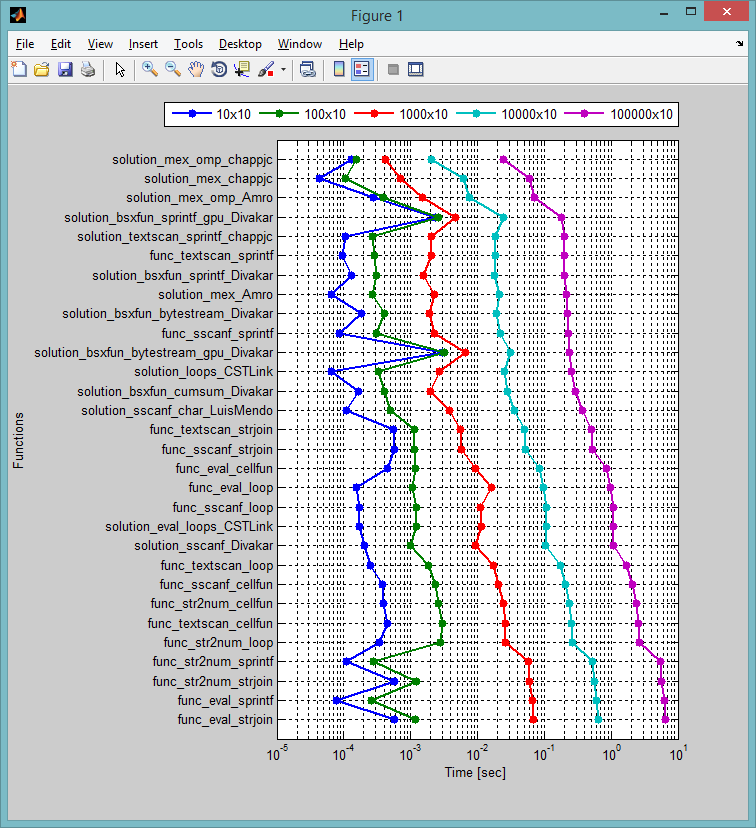
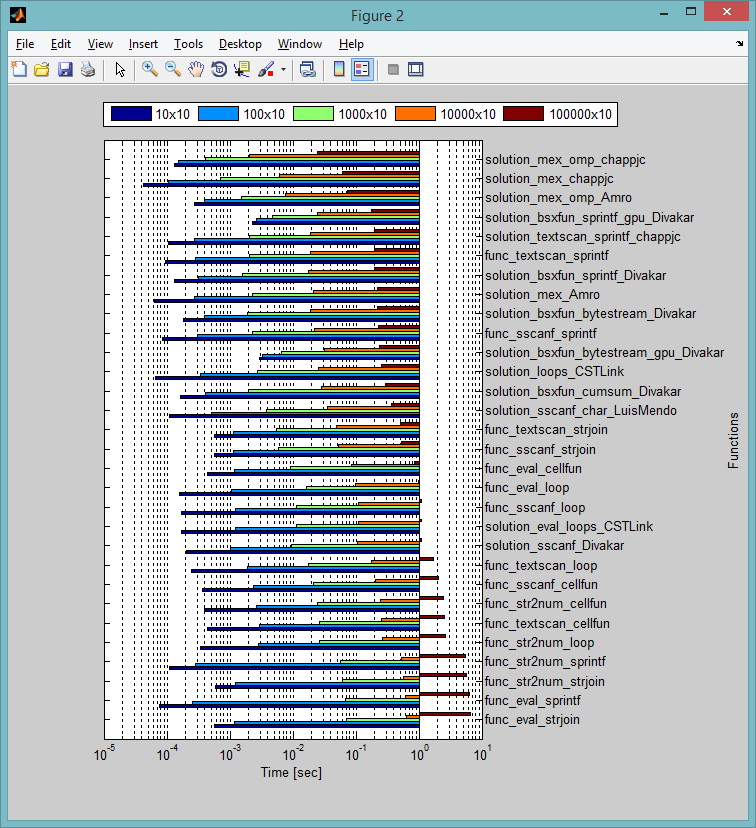
>> t
t =
func nrows ncols time
________________________________________ _____ _____ __________
'func_eval_cellfun' 10 10 0.00044645
'func_eval_loop' 10 10 0.0001554
'func_eval_sprintf' 10 10 7.6547e-05
'func_eval_strjoin' 10 10 0.00056739
'func_sscanf_cellfun' 10 10 0.00037247
'func_sscanf_loop' 10 10 0.00017182
'func_sscanf_sprintf' 10 10 8.4928e-05
'func_sscanf_strjoin' 10 10 0.00056388
'func_str2num_cellfun' 10 10 0.00039231
'func_str2num_loop' 10 10 0.00033852
'func_str2num_sprintf' 10 10 0.00010862
'func_str2num_strjoin' 10 10 0.00057953
'func_textscan_cellfun' 10 10 0.00044585
'func_textscan_loop' 10 10 0.00024666
'func_textscan_sprintf' 10 10 9.4507e-05
'func_textscan_strjoin' 10 10 0.00056123
'solution_bsxfun_bytestream_Divakar' 10 10 0.00018166
'solution_bsxfun_bytestream_gpu_Divakar' 10 10 0.0029487
'solution_bsxfun_cumsum_Divakar' 10 10 0.00016396
'solution_bsxfun_sprintf_Divakar' 10 10 0.00012932
'solution_bsxfun_sprintf_gpu_Divakar' 10 10 0.002315
'solution_eval_loops_CSTLink' 10 10 0.00017191
'solution_loops_CSTLink' 10 10 6.5514e-05
'solution_mex_Amro' 10 10 6.4487e-05
'solution_mex_chappjc' 10 10 4.2507e-05
'solution_mex_omp_Amro' 10 10 0.00027411
'solution_mex_omp_chappjc' 10 10 0.00013017
'solution_sscanf_Divakar' 10 10 0.00020458
'solution_sscanf_char_LuisMendo' 10 10 0.00011144
'solution_textscan_sprintf_chappjc' 10 10 0.00010528
'func_eval_cellfun' 100 10 0.0011801
'func_eval_loop' 100 10 0.001059
'func_eval_sprintf' 100 10 0.00025547
'func_eval_strjoin' 100 10 0.0011824
'func_sscanf_cellfun' 100 10 0.0023356
'func_sscanf_loop' 100 10 0.0012338
'func_sscanf_sprintf' 100 10 0.00031012
'func_sscanf_strjoin' 100 10 0.0011334
'func_str2num_cellfun' 100 10 0.002635
'func_str2num_loop' 100 10 0.0028056
'func_str2num_sprintf' 100 10 0.00027899
'func_str2num_strjoin' 100 10 0.0012117
'func_textscan_cellfun' 100 10 0.0029546
'func_textscan_loop' 100 10 0.0018652
'func_textscan_sprintf' 100 10 0.00028506
'func_textscan_strjoin' 100 10 0.001125
'solution_bsxfun_bytestream_Divakar' 100 10 0.00040027
'solution_bsxfun_bytestream_gpu_Divakar' 100 10 0.0032536
'solution_bsxfun_cumsum_Divakar' 100 10 0.00041019
'solution_bsxfun_sprintf_Divakar' 100 10 0.00031089
'solution_bsxfun_sprintf_gpu_Divakar' 100 10 0.0026271
'solution_eval_loops_CSTLink' 100 10 0.0012294
'solution_loops_CSTLink' 100 10 0.00033501
'solution_mex_Amro' 100 10 0.00027069
'solution_mex_chappjc' 100 10 0.00010682
'solution_mex_omp_Amro' 100 10 0.00039385
'solution_mex_omp_chappjc' 100 10 0.00015232
'solution_sscanf_Divakar' 100 10 0.0010108
'solution_sscanf_char_LuisMendo' 100 10 0.00050153
'solution_textscan_sprintf_chappjc' 100 10 0.00026958
'func_eval_cellfun' 1000 10 0.0092491
'func_eval_loop' 1000 10 0.016145
'func_eval_sprintf' 1000 10 0.067573
'func_eval_strjoin' 1000 10 0.070024
'func_sscanf_cellfun' 1000 10 0.020954
'func_sscanf_loop' 1000 10 0.011224
'func_sscanf_sprintf' 1000 10 0.0022546
'func_sscanf_strjoin' 1000 10 0.0058568
'func_str2num_cellfun' 1000 10 0.024699
'func_str2num_loop' 1000 10 0.02645
'func_str2num_sprintf' 1000 10 0.05713
'func_str2num_strjoin' 1000 10 0.060093
'func_textscan_cellfun' 1000 10 0.02592
'func_textscan_loop' 1000 10 0.017589
'func_textscan_sprintf' 1000 10 0.0020249
'func_textscan_strjoin' 1000 10 0.0055364
'solution_bsxfun_bytestream_Divakar' 1000 10 0.0018817
'solution_bsxfun_bytestream_gpu_Divakar' 1000 10 0.0066003
'solution_bsxfun_cumsum_Divakar' 1000 10 0.001982
'solution_bsxfun_sprintf_Divakar' 1000 10 0.0015578
'solution_bsxfun_sprintf_gpu_Divakar' 1000 10 0.0046952
'solution_eval_loops_CSTLink' 1000 10 0.011481
'solution_loops_CSTLink' 1000 10 0.0027254
'solution_mex_Amro' 1000 10 0.0022698
'solution_mex_chappjc' 1000 10 0.0006967
'solution_mex_omp_Amro' 1000 10 0.0015025
'solution_mex_omp_chappjc' 1000 10 0.00041463
'solution_sscanf_Divakar' 1000 10 0.0093785
'solution_sscanf_char_LuisMendo' 1000 10 0.0038031
'solution_textscan_sprintf_chappjc' 1000 10 0.0020323
'func_eval_cellfun' 10000 10 0.083676
'func_eval_loop' 10000 10 0.098798
'func_eval_sprintf' 10000 10 0.60429
'func_eval_strjoin' 10000 10 0.63656
'func_sscanf_cellfun' 10000 10 0.20675
'func_sscanf_loop' 10000 10 0.1088
'func_sscanf_sprintf' 10000 10 0.021725
'func_sscanf_strjoin' 10000 10 0.052341
'func_str2num_cellfun' 10000 10 0.24192
'func_str2num_loop' 10000 10 0.26538
'func_str2num_sprintf' 10000 10 0.53451
'func_str2num_strjoin' 10000 10 0.56759
'func_textscan_cellfun' 10000 10 0.25474
'func_textscan_loop' 10000 10 0.17402
'func_textscan_sprintf' 10000 10 0.018799
'func_textscan_strjoin' 10000 10 0.04965
'solution_bsxfun_bytestream_Divakar' 10000 10 0.019165
'solution_bsxfun_bytestream_gpu_Divakar' 10000 10 0.031283
'solution_bsxfun_cumsum_Divakar' 10000 10 0.027986
'solution_bsxfun_sprintf_Divakar' 10000 10 0.017761
'solution_bsxfun_sprintf_gpu_Divakar' 10000 10 0.024821
'solution_eval_loops_CSTLink' 10000 10 0.10885
'solution_loops_CSTLink' 10000 10 0.025136
'solution_mex_Amro' 10000 10 0.021374
'solution_mex_chappjc' 10000 10 0.0060774
'solution_mex_omp_Amro' 10000 10 0.0076461
'solution_mex_omp_chappjc' 10000 10 0.002058
'solution_sscanf_Divakar' 10000 10 0.10503
'solution_sscanf_char_LuisMendo' 10000 10 0.035483
'solution_textscan_sprintf_chappjc' 10000 10 0.018772
'func_eval_cellfun' 1e+05 10 0.85115
'func_eval_loop' 1e+05 10 0.97977
'func_eval_sprintf' 1e+05 10 6.2422
'func_eval_strjoin' 1e+05 10 6.5012
'func_sscanf_cellfun' 1e+05 10 2.0761
'func_sscanf_loop' 1e+05 10 1.0865
'func_sscanf_sprintf' 1e+05 10 0.22618
'func_sscanf_strjoin' 1e+05 10 0.53146
'func_str2num_cellfun' 1e+05 10 2.4041
'func_str2num_loop' 1e+05 10 2.6431
'func_str2num_sprintf' 1e+05 10 5.4
'func_str2num_strjoin' 1e+05 10 5.6967
'func_textscan_cellfun' 1e+05 10 2.5696
'func_textscan_loop' 1e+05 10 1.7175
'func_textscan_sprintf' 1e+05 10 0.19759
'func_textscan_strjoin' 1e+05 10 0.50314
'solution_bsxfun_bytestream_Divakar' 1e+05 10 0.21884
'solution_bsxfun_bytestream_gpu_Divakar' 1e+05 10 0.23607
'solution_bsxfun_cumsum_Divakar' 1e+05 10 0.29511
'solution_bsxfun_sprintf_Divakar' 1e+05 10 0.19882
'solution_bsxfun_sprintf_gpu_Divakar' 1e+05 10 0.17923
'solution_eval_loops_CSTLink' 1e+05 10 1.0943
'solution_loops_CSTLink' 1e+05 10 0.2534
'solution_mex_Amro' 1e+05 10 0.21575
'solution_mex_chappjc' 1e+05 10 0.060666
'solution_mex_omp_Amro' 1e+05 10 0.072168
'solution_mex_omp_chappjc' 1e+05 10 0.024385
'solution_sscanf_Divakar' 1e+05 10 1.0992
'solution_sscanf_char_LuisMendo' 1e+05 10 0.36688
'solution_textscan_sprintf_chappjc' 1e+05 10 0.19755
ceci s'appuie sur la solution MEX D'Amro. Puisque le problème tel que défini par CST-Link est si étroitement limité, une mise en œuvre rapide peut être faite en sacrifiant robustesse et renoncement à la manipulation d'erreur. Par conséquent, formater l'entrée comme spécifié!
remplacez la boucle principale dans la source D'Amro par ce qui suit pour une vitesse ~4x, Sans multi-threading ( source complète):
// extract numbers from strings
for (mwIndex idx=0, i=0; idx<n_words; ++idx) {
std::string str = getString(cellstr, idx);
std::string::const_iterator istr = str.cbegin();
for (; istr != str.cend(); ++istr) {
if (*istr < '0' || *istr > '9')
{
++i;
continue;
}
out[i] *= 10;
out[i] += *istr - '0';
}
++i;
}
on peut faire plus d'optimisation manuelle, mais je vais me coucher. Aussi, je suis la planification à la version multi-threaded à un certain point, mais il est assez simple d'ajouter le pragma.
Repères (mise à JOUR de T-moins de 12 heures jusqu'à la fin de la période de grâce)
Repères avec Amro dernier package de fonctions, ainsi que Ben Voigt solution de montrer des temps différents sur différentes machines, mais pour ce que ça vaut, il semble qu'il y est un véritable égalité entre quelques solutions. Sur mon ordinateur portable i7 avec r2014 a 64-bit sur Windows 8 (sur CUDA), my textscan, Divakar's latest et Ben Voigt's solutions sont les meilleures, avec des différences de performance indistinguables. "All loops" de CST-Link est très proche, mais toujours un cheveu plus lent que les autres. Ces benchmarks utilisent jusqu'à 1e6 cordes. la taille du réseau de cellules détermine la méthode la plus rapide.
en sortant les solutions MEX (et GPU parce que mon de mon ordinateur portable), les solutions sont placées comme suit pour divers nombres de lignes. Encore une fois, les résultats suggèrent que la méthode appropriée dépend du nombre de lignes:
i7 16GB R2014a
Solution 1e6 5e5 1e5 1e4 1e3 100
____________________________________ ____ ____ ____ ____ ____ ____
'solution_textscan_sprintf_chappjc' 1 2 2 5 5 4
'solution_bsxfun_sprintf_Divakar' 2 1 3 2 1 8
'func_voigt_loop' 3 3 5 1 2 1
'func_textscan_sprintf' 4 4 4 4 6 3
'solution_bsxfun_bytestream_Divakar' 5 5 6 3 3 10
'solution_loops_CSTLink' 6 7 7 7 8 6
'func_sscanf_sprintf' 7 6 1 6 7 7
'solution_bsxfun_cumsum_Divakar' 8 8 8 8 4 9
'solution_sscanf_char_LuisMendo' 9 9 9 9 9 11
'func_textscan_strjoin' 10 10 15 10 10 16
'func_sscanf_strjoin' 11 11 10 11 11 19
'func_eval_cellfun' 12 12 13 12 12 18
'func_eval_loop' 13 13 11 13 13 12
'solution_eval_loops_CSTLink' 14 15 14 14 14 13
'func_sscanf_loop' 15 14 12 15 15 15
'func_textscan_loop' 16 18 19 18 18 21
'func_sscanf_cellfun' 17 17 16 17 17 22
'func_str2num_cellfun' 18 19 18 19 19 23
'func_str2num_loop' 19 20 20 20 20 24
'solution_sscanf_Divakar' 20 16 17 16 16 20
'func_textscan_cellfun' 21 21 21 21 21 25
'func_str2num_sprintf' 22 23 23 22 22 5
'func_str2num_strjoin' 23 24 25 23 23 17
'func_eval_sprintf' 24 22 24 24 24 2
'func_eval_strjoin' 25 25 22 25 25 14
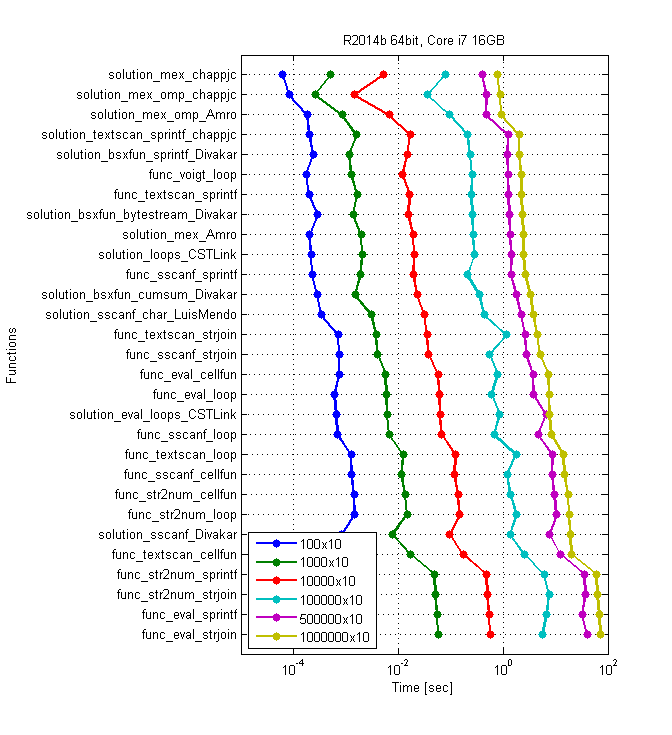
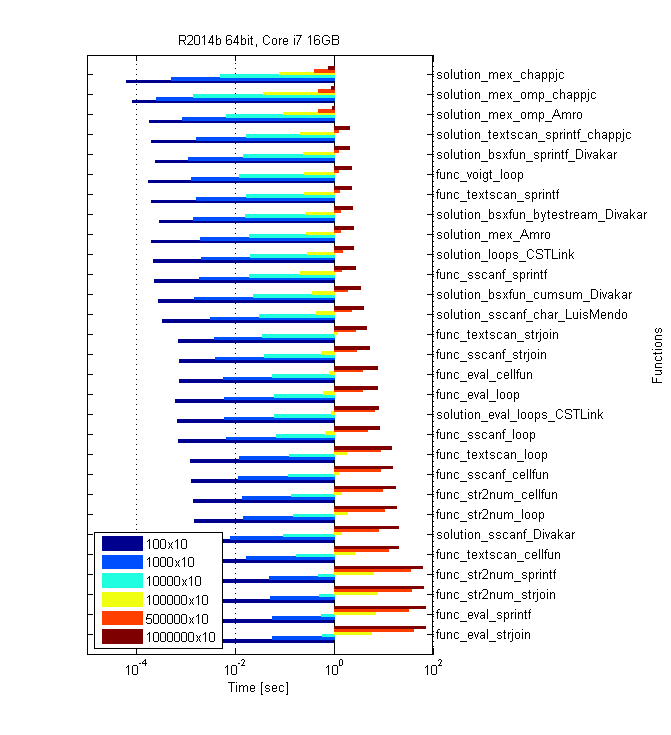
>> t
t =
func nrows ncols time
____________________________________ _____ _____ __________
'func_eval_cellfun' 100 10 0.00074097
'func_eval_loop' 100 10 0.0006137
'func_eval_sprintf' 100 10 0.00017814
'func_eval_strjoin' 100 10 0.00068062
'func_sscanf_cellfun' 100 10 0.0012905
'func_sscanf_loop' 100 10 0.00069992
'func_sscanf_sprintf' 100 10 0.00022678
'func_sscanf_strjoin' 100 10 0.00075428
'func_str2num_cellfun' 100 10 0.0014366
'func_str2num_loop' 100 10 0.0014904
'func_str2num_sprintf' 100 10 0.00020667
'func_str2num_strjoin' 100 10 0.00073786
'func_textscan_cellfun' 100 10 0.0018517
'func_textscan_loop' 100 10 0.0012629
'func_textscan_sprintf' 100 10 0.00020092
'func_textscan_strjoin' 100 10 0.00071305
'func_voigt_loop' 100 10 0.00017711
'solution_bsxfun_bytestream_Divakar' 100 10 0.00029257
'solution_bsxfun_cumsum_Divakar' 100 10 0.00028395
'solution_bsxfun_sprintf_Divakar' 100 10 0.00023879
'solution_eval_loops_CSTLink' 100 10 0.00066461
'solution_loops_CSTLink' 100 10 0.00021923
'solution_mex_Amro' 100 10 0.00020502
'solution_mex_chappjc' 100 10 6.3164e-05
'solution_mex_omp_Amro' 100 10 0.00018224
'solution_mex_omp_chappjc' 100 10 8.2565e-05
'solution_sscanf_Divakar' 100 10 0.00084008
'solution_sscanf_char_LuisMendo' 100 10 0.00033844
'solution_textscan_sprintf_chappjc' 100 10 0.00020396
'func_eval_cellfun' 1000 10 0.0058036
'func_eval_loop' 1000 10 0.0060269
'func_eval_sprintf' 1000 10 0.055797
'func_eval_strjoin' 1000 10 0.057631
'func_sscanf_cellfun' 1000 10 0.011712
'func_sscanf_loop' 1000 10 0.0067405
'func_sscanf_sprintf' 1000 10 0.0019112
'func_sscanf_strjoin' 1000 10 0.0040608
'func_str2num_cellfun' 1000 10 0.013712
'func_str2num_loop' 1000 10 0.014961
'func_str2num_sprintf' 1000 10 0.04916
'func_str2num_strjoin' 1000 10 0.051823
'func_textscan_cellfun' 1000 10 0.017256
'func_textscan_loop' 1000 10 0.012454
'func_textscan_sprintf' 1000 10 0.0016489
'func_textscan_strjoin' 1000 10 0.0038387
'func_voigt_loop' 1000 10 0.0012892
'solution_bsxfun_bytestream_Divakar' 1000 10 0.0013951
'solution_bsxfun_cumsum_Divakar' 1000 10 0.0015138
'solution_bsxfun_sprintf_Divakar' 1000 10 0.0011496
'solution_eval_loops_CSTLink' 1000 10 0.0061538
'solution_loops_CSTLink' 1000 10 0.0020528
'solution_mex_Amro' 1000 10 0.0019629
'solution_mex_chappjc' 1000 10 0.00051825
'solution_mex_omp_Amro' 1000 10 0.00085117
'solution_mex_omp_chappjc' 1000 10 0.00025825
'solution_sscanf_Divakar' 1000 10 0.0078551
'solution_sscanf_char_LuisMendo' 1000 10 0.0031104
'solution_textscan_sprintf_chappjc' 1000 10 0.0016144
'func_eval_cellfun' 10000 10 0.05772
'func_eval_loop' 10000 10 0.061705
'func_eval_sprintf' 10000 10 0.54464
'func_eval_strjoin' 10000 10 0.57007
'func_sscanf_cellfun' 10000 10 0.1192
'func_sscanf_loop' 10000 10 0.068017
'func_sscanf_sprintf' 10000 10 0.019622
'func_sscanf_strjoin' 10000 10 0.038232
'func_str2num_cellfun' 10000 10 0.13811
'func_str2num_loop' 10000 10 0.14812
'func_str2num_sprintf' 10000 10 0.48726
'func_str2num_strjoin' 10000 10 0.50528
'func_textscan_cellfun' 10000 10 0.17378
'func_textscan_loop' 10000 10 0.1241
'func_textscan_sprintf' 10000 10 0.016595
'func_textscan_strjoin' 10000 10 0.035599
'func_voigt_loop' 10000 10 0.012136
'solution_bsxfun_bytestream_Divakar' 10000 10 0.015908
'solution_bsxfun_cumsum_Divakar' 10000 10 0.02301
'solution_bsxfun_sprintf_Divakar' 10000 10 0.014862
'solution_eval_loops_CSTLink' 10000 10 0.063188
'solution_loops_CSTLink' 10000 10 0.020153
'solution_mex_Amro' 10000 10 0.019252
'solution_mex_chappjc' 10000 10 0.0051221
'solution_mex_omp_Amro' 10000 10 0.0066551
'solution_mex_omp_chappjc' 10000 10 0.0014584
'solution_sscanf_Divakar' 10000 10 0.096345
'solution_sscanf_char_LuisMendo' 10000 10 0.031047
'solution_textscan_sprintf_chappjc' 10000 10 0.016736
'func_eval_cellfun' 1e+05 10 0.78876
'func_eval_loop' 1e+05 10 0.6119
'func_eval_sprintf' 1e+05 10 6.7603
'func_eval_strjoin' 1e+05 10 5.7204
'func_sscanf_cellfun' 1e+05 10 1.2096
'func_sscanf_loop' 1e+05 10 0.68303
'func_sscanf_sprintf' 1e+05 10 0.21101
'func_sscanf_strjoin' 1e+05 10 0.55226
'func_str2num_cellfun' 1e+05 10 1.411
'func_str2num_loop' 1e+05 10 1.8229
'func_str2num_sprintf' 1e+05 10 6.1474
'func_str2num_strjoin' 1e+05 10 7.551
'func_textscan_cellfun' 1e+05 10 2.5898
'func_textscan_loop' 1e+05 10 1.7934
'func_textscan_sprintf' 1e+05 10 0.25421
'func_textscan_strjoin' 1e+05 10 1.1762
'func_voigt_loop' 1e+05 10 0.25602
'solution_bsxfun_bytestream_Divakar' 1e+05 10 0.265
'solution_bsxfun_cumsum_Divakar' 1e+05 10 0.35656
'solution_bsxfun_sprintf_Divakar' 1e+05 10 0.23481
'solution_eval_loops_CSTLink' 1e+05 10 0.86425
'solution_loops_CSTLink' 1e+05 10 0.28436
'solution_mex_Amro' 1e+05 10 0.27104
'solution_mex_chappjc' 1e+05 10 0.078901
'solution_mex_omp_Amro' 1e+05 10 0.096553
'solution_mex_omp_chappjc' 1e+05 10 0.03679
'solution_sscanf_Divakar' 1e+05 10 1.3818
'solution_sscanf_char_LuisMendo' 1e+05 10 0.43994
'solution_textscan_sprintf_chappjc' 1e+05 10 0.21271
'func_eval_cellfun' 5e+05 10 3.7658
'func_eval_loop' 5e+05 10 3.8106
'func_eval_sprintf' 5e+05 10 32.383
'func_eval_strjoin' 5e+05 10 40.451
'func_sscanf_cellfun' 5e+05 10 8.5704
'func_sscanf_loop' 5e+05 10 4.707
'func_sscanf_sprintf' 5e+05 10 1.4362
'func_sscanf_strjoin' 5e+05 10 2.8301
'func_str2num_cellfun' 5e+05 10 9.6439
'func_str2num_loop' 5e+05 10 10.453
'func_str2num_sprintf' 5e+05 10 35.818
'func_str2num_strjoin' 5e+05 10 37.277
'func_textscan_cellfun' 5e+05 10 12.418
'func_textscan_loop' 5e+05 10 8.8237
'func_textscan_sprintf' 5e+05 10 1.2793
'func_textscan_strjoin' 5e+05 10 2.6496
'func_voigt_loop' 5e+05 10 1.2486
'solution_bsxfun_bytestream_Divakar' 5e+05 10 1.324
'solution_bsxfun_cumsum_Divakar' 5e+05 10 1.8229
'solution_bsxfun_sprintf_Divakar' 5e+05 10 1.2113
'solution_eval_loops_CSTLink' 5e+05 10 6.5759
'solution_loops_CSTLink' 5e+05 10 1.4583
'solution_mex_Amro' 5e+05 10 1.3718
'solution_mex_chappjc' 5e+05 10 0.39711
'solution_mex_omp_Amro' 5e+05 10 0.48046
'solution_mex_omp_chappjc' 5e+05 10 0.48174
'solution_sscanf_Divakar' 5e+05 10 7.7943
'solution_sscanf_char_LuisMendo' 5e+05 10 2.2332
'solution_textscan_sprintf_chappjc' 5e+05 10 1.2399
'func_eval_cellfun' 1e+06 10 7.3884
'func_eval_loop' 1e+06 10 7.5519
'func_eval_sprintf' 1e+06 10 69.868
'func_eval_strjoin' 1e+06 10 71.964
'func_sscanf_cellfun' 1e+06 10 15.061
'func_sscanf_loop' 1e+06 10 8.4163
'func_sscanf_sprintf' 1e+06 10 2.7099
'func_sscanf_strjoin' 1e+06 10 5.1453
'func_str2num_cellfun' 1e+06 10 17.42
'func_str2num_loop' 1e+06 10 18.165
'func_str2num_sprintf' 1e+06 10 60.902
'func_str2num_strjoin' 1e+06 10 63.579
'func_textscan_cellfun' 1e+06 10 20.423
'func_textscan_loop' 1e+06 10 14.309
'func_textscan_sprintf' 1e+06 10 2.2853
'func_textscan_strjoin' 1e+06 10 4.5216
'func_voigt_loop' 1e+06 10 2.2443
'solution_bsxfun_bytestream_Divakar' 1e+06 10 2.3495
'solution_bsxfun_cumsum_Divakar' 1e+06 10 3.3843
'solution_bsxfun_sprintf_Divakar' 1e+06 10 2.0311
'solution_eval_loops_CSTLink' 1e+06 10 7.7524
'solution_loops_CSTLink' 1e+06 10 2.4947
'solution_mex_Amro' 1e+06 10 2.486
'solution_mex_chappjc' 1e+06 10 0.76551
'solution_mex_omp_Amro' 1e+06 10 0.92226
'solution_mex_omp_chappjc' 1e+06 10 0.88736
'solution_sscanf_Divakar' 1e+06 10 19.673
'solution_sscanf_char_LuisMendo' 1e+06 10 3.8578
'solution_textscan_sprintf_chappjc' 1e+06 10 2.0074
Suivant...
X5550 24GB R2014b
L'ordre est différent, mais les différences sont encore insignifiants.
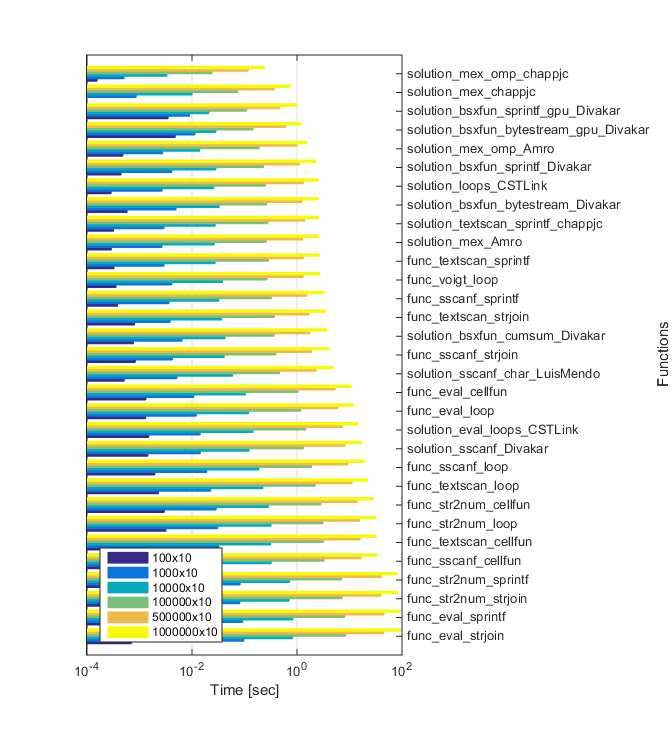
Timings de dépasser les 30 000 limite de caractères, mais je peux les poster quelque part, si voulu. L'ordre est clair.
je suggère CST-Lien abstraction de toutes ces mesures en décider.
bien sûr, le MEX solutions à la règle. La solution ci-dessus avec std::string::const_iterator istr est rapide, encore plus rapide avec OpenMP. GCC 4.9.1 (pthreads) et VS2013 ont des performances comparables pour ce code. Filetée source ici.
la solution suivante semble fonctionner:
function array_of_numbers = char_and_sscanf_solution(list_of_words)
s = char(list_of_words);
s(s==95) = 32; %// 95 is '_'; 32 is ' '
s = [ s repmat(32, numel(list_of_words), 1) ];
array_of_numbers = reshape(sscanf(s.','%i '), [], numel(list_of_words)).'/1000;
les résultats de l'analyse comparative à l'aide de referee_timing.m et referee_test_case.m:
Generating 10000-words test case...
Timing 10000-words test case...
eval_and_loops_solution: 0.190642[s]
single_sscanf_solution: 0.234413[s]
approach1: 0.073901[s]
char_and_sscanf_solution: 0.068311[s]
Generating 100000-words test case...
Timing 100000-words test case...
eval_and_loops_solution: 1.957728[s]
single_sscanf_solution: 2.426764[s]
approach1: 0.766020[s]
char_and_sscanf_solution: 0.706387[s]
Generating 1000000-words test case...
Timing 1000000-words test case...
eval_and_loops_solution: 18.975746[s]
char_and_sscanf_solution: 7.147229[s]
informations de l'Ordinateur:
Matlab R2010b
Windows 7 Home Premium 64 bits Service Pack 1
Pentium (R)Double Core CPU T4300 2.10 GHz
4 GO RAM
j'aimerais appliquer sprintf avec un liste séparée par des virgules entrée pour générer un unique, entièrement délimité par des 1D chaîne de caractères (avec séparateur à la fin de chaque ligne/chaîne), et ensuite utiliser textscan pour retirer les entiers:
extractIntsSprintfTextScan.m
function M = extractIntsSprintfTextScan(list_of_words)
% optimized lines, see below for explanation of each op
M = textscan(sprintf('%s_',C{:}),'%.0f', 'Delimiter','_');
M = reshape(M{1}, [], numel(C)).';
% cell to string, adding _ suffix
% s = sprintf('%s_',list_of_words{:});
% extract integers given _ as delimiter
% C = textscan(s,'%u','Delimiter','_','CollectOutput',1); % can also use %d for signed
% C = textscan(s,'%.0f_','CollectOutput',1); % a little faster to put _ in the pattern
% matrix form
% M = reshape(C{1},[],numel(list_of_words)).'/1000; % remove transpose for faster output
end
Repères (précédent timings maintenant obsolète, voir sprintf+textscan la solution Amro référence du poste au lieu de cela)
Machine
MATLAB R2014 b 64-bit
Windows 7 64 bits
24 GB RAM
Double Xeon X5550 (2,67 GHZ, 8 noyaux physiques)
UPDATE: Change le type de sortie en double à partir d'un type entier. Relancer les benchmarks.
UPDATE 2: Changer le spécificateur de format de '%f''%.0f', peut-être l'autoriser pour accélérer la numérisation depuis sans décimales sont demandés. Augmentation N = 100e3; (voir GitHub Gist).
UPDATE 3: de Nouveaux repères avec la version 2 de la CST-Lien de fonctions de temporisation (voir GitHub Gist avec l'utilisation suggérée de arbitre_timing.m.)
UPDATE 4: ajouter la solution de Luis. Notez que les résultats fluctuent, puisque les données sont générées de manière aléatoire.
UPDATE 5: Optimisation réglages -- voir Amro analyse comparative de la poste.
Défi accepté! Voici mon implémentation la plus rapide jusqu'à présent, et oui c'est un fichier c++:)
solution_mex.rpc
#include "mex.h"
#include <vector>
#include <string>
#include <sstream>
#include <algorithm>
#include <iterator>
namespace {
// get i-th string from cell-array of strings
std::string getString(const mxArray *cellstr, mwIndex idx)
{
mxArray *arr = mxGetCell(cellstr, idx);
if (arr == NULL) mexErrMsgIdAndTxt("mex:err", "null/uninitialized");
if (!mxIsChar(arr)) mexErrMsgIdAndTxt("mex:err", "not a string");
char *cstr = mxArrayToString(arr);
if (cstr == NULL) mexErrMsgIdAndTxt("mex:err", "null");
std::string str(cstr);
mxFree(cstr);
return str;
}
// count of numbers in char-delimited string
mwSize count_numbers(const std::string &s)
{
return std::count(s.begin(), s.end(), '_') + 1;
}
// parse numbers
template <typename T>
void parseNumbers(const mxArray *cellstr, const mwSize len, std::vector<T> &v)
{
// cell-array of strings
std::vector<std::string> vs;
vs.reserve(len);
for (mwIndex idx=0; idx<len; ++idx) {
vs.push_back(getString(cellstr, idx));
}
// join vector of strings into one
std::stringstream ss;
std::copy(vs.begin(), vs.end(),
std::ostream_iterator<std::string>(ss, "_"));
// split string into numbers (separated by single-char delimiter)
T num;
while (ss >> num) {
v.push_back(num);
ss.ignore(1);
}
}
};
void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])
{
// validate inputs
if (nrhs!=1 || nlhs>1) mexErrMsgIdAndTxt("mex:err", "wrong num args");
if (!mxIsCell(prhs[0])) mexErrMsgIdAndTxt("mex:err", "not cell");
// allocate output matrix
mwSize len = mxGetNumberOfElements(prhs[0]);
mwSize sz = (len > 0) ? count_numbers(getString(prhs[0],0)) : 0;
plhs[0] = mxCreateNumericMatrix(sz, len, mxDOUBLE_CLASS, mxREAL);
if (plhs[0] == NULL) mexErrMsgIdAndTxt("mex:err", "null");
if (len == 0 || sz == 0) return;
// parse cell array into numbers
std::vector<int> v;
v.reserve(len*sz);
parseNumbers(prhs[0], len, v);
if (v.size() != (len*sz)) mexErrMsgIdAndTxt("mex:err", "wrong size");
// copy numbers into output matrix
std::copy(v.begin(), v.end(), mxGetPr(plhs[0]));
}
le code est simple à lire; j'utilise la bibliothèque standard STL là où c'est possible (pas de trucs cochons), plus il y a beaucoup de vérifications et de validation des entrées, donc il devrait être robuste aussi longtemps que vous suivez le format d'entrée décrit dans la question.
je vais mettre à jour avec quelques repères plus tard, mais pour l'instant vous pouvez le tester sur votre propre et de les comparer par rapport aux autres solutions...
Remarque ci-dessus MEX-fonction renvoie une matrice de taille n_numbers * n_words, donc vous voudrez transposer le résultat.
Voici une fonction wrapper M-que vous pouvez utiliser pour exécuter sous le programme arbitre:
solution_mex.m
function array_of_numbers = mex_solution(list_of_words)
array_of_numbers = solution_mex(list_of_words).';
end
EDIT#1
simplifions un peu le code; cette version utilise beaucoup moins de mémoire en traitant une chaîne à la fois, et en plaçant le résultat directement dans la matrice de sortie:
solution_mex.rpc
#include "mex.h"
#include <string>
#include <sstream>
#include <algorithm>
namespace {
std::string getString(const mxArray *cellstr, const mwIndex idx)
{
// get i-th string from cell-array of strings
mxArray *arr = mxGetCell(cellstr, idx);
if (!arr || !mxIsChar(arr)) mexErrMsgIdAndTxt("mex:err", "not a string");
char *cstr = mxArrayToString(arr);
if (cstr == NULL) mexErrMsgIdAndTxt("mex:err", "null");
std::string str(cstr);
mxFree(cstr);
return str;
}
mwSize count_numbers(const std::string &s)
{
// count of numbers in char-delimited string
return std::count(s.begin(), s.end(), '_') + 1;
}
};
void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])
{
// validate inputs
if (nrhs!=1 || nlhs>1) mexErrMsgIdAndTxt("mex:err", "wrong num args");
if (!mxIsCell(prhs[0])) mexErrMsgIdAndTxt("mex:err", "not a cell");
// determine sizes
const mxArray *cellstr = prhs[0];
const mwSize n_words = mxGetNumberOfElements(cellstr);
const mwSize n_nums = (n_words > 0) ?
count_numbers(getString(cellstr,0)) : 0;
// allocate output matrix
plhs[0] = mxCreateDoubleMatrix(n_nums, n_words, mxREAL);
if (plhs[0] == NULL) mexErrMsgIdAndTxt("mex:err", "null");
if (n_words == 0 || n_nums == 0) return;
double *out = mxGetPr(plhs[0]);
// extract numbers from strings
for (mwIndex idx=0, i=0; idx<n_words; ++idx) {
std::istringstream ss(getString(cellstr, idx));
int num;
while(ss >> num) {
out[i++] = num;
ss.ignore(1);
}
}
}
EDIT#2 (OpenMP)
Prochaine étape, nous allons le rendre multi-thread; Nous pouvons le faire implicitement en utilisant OpenMP par le simple ajout de deux lignes de code! Je suis en parallélisme sur chaque corde.
nous ajoutons D'abord le omp parallel for pragma, puis nous faisons la variable d'index i privé à chaque thread, de cette façon les threads connaissent l'index de démarrage de la colonne.
Dans le code précédent de edit#1, il suffit de remplacer la dernière boucle avec:
// extract numbers from strings
#pragma omp parallel for
for (mwIndex idx=0; idx<n_words; ++idx) {
mwIndex i = idx*n_nums; // starting index for i-th column
std::istringstream ss(getString(cellstr, idx));
int num;
while(ss >> num) {
out[i++] = num;
ss.ignore(1);
}
}
j'exécute R2014 sur Windows x64, et j'ai essayé de compiler avec VS2013 et MinGW-w64 GCC 4.9.1. Permettez-moi de souligner que la version compilée par GCC est beaucoup plus rapide que toutes les solutions jusqu'à présent:
% compile with MinGW-w64
>> mex -largeArrayDims -f mingwopts.bat solution_mex.cpp -output solution_mex_gcc
% set appropriate number of threads
>> setenv('OMP_NUM_THREADS','4');
% quick benchmark
>> timeit(@() solution_mex_gcc(repmat({'02_04_04_52_23_14_54_672_0'},1e6,1)).')
ans =
0.6658
(Proposition la Plus récente)
ce genre de solution élimine la dernière partie de ma solution anti-MATLAB spécifique au MATLAB; pur byte-scanning, loop-in-loop, mem-attributing stuff:
%'all_loops.m'
function array_of_numbers = all_loops(list_of_words)
%'Precalculate important numbers'
n_numbers = 1 + sum(list_of_words{1}=='_');
n_words = numel(list_of_words);
%'Allocate memory'
array_of_numbers = zeros(n_numbers, n_words);
slice_of_numbers = zeros(n_numbers, 1);
%'Loop trough chunks of cell array'
for k = 1:n_words
str = list_of_words{k};
pos_max = size(str, 2);
value = 0;
index = 1;
for pos = 1:pos_max
if str(pos) == '_'
slice_of_numbers(index) = value;
value = 0;
index = index + 1;
else
value = 10*value + (str(pos) - '0');
end;
slice_of_numbers(index) = value; %'almost forgot'
end;
array_of_numbers(:, k) = slice_of_numbers;
end;
%'This is a waste of memory, but is kind of required'
array_of_numbers = transpose(array_of_numbers / 1000);
end
(Benchmarking) Pour la configuration suivante (obtenue à partir de configinfo.m)
MATLAB configuration information CPU: x86 Family 6 Model 58 Stepping 9, GenuineIntel
This data was gathered on: 24-Oct-2014 14:19:31 The measured CPU speed is: 2600 MHz
MATLAB version: 7.14.0.739 (R2012a) Number of processors: 4
MATLAB root: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx RAM: 3289 MB
MATLAB accelerator enabled Swap space: 6576 MB
MATLAB JIT: enabled Microsoft Windows 7
MATLAB assertions: disabled Number of cores: 2
MATLAB Desktop: enabled Number of threads: 2
les résultats suivants ont été obtenus (3ème course):
Generating 10000-words test case...
Timing 1000000-words test case...
approach4: Error - Out of memory. Type HELP MEMORY for your options.
approach1: Error - Out of memory. Type HELP MEMORY for your options.
single_sscanf_solution: Error - Out of memory. Type HELP MEMORY for your options.
char_and_sscanf_solution: 5.076296[s]
extractIntsSprintfTextScan: 4.328066[s]
all_loops: 1.795730[s]
eval_and_loops_solution: 10.027541[s]
Generating 100000-words test case...
Timing 100000-words test case...
approach4: 0.252107[s]
approach1: 0.370727[s]
single_sscanf_solution: 1.364936[s]
char_and_sscanf_solution: 0.515599[s]
extractIntsSprintfTextScan: 0.444586[s]
all_loops: 0.179575[s]
eval_and_loops_solution: 1.010240[s]
Generating 10000-words test case...
Timing 10000-words test case...
approach4: 0.026642[s]
approach1: 0.039550[s]
single_sscanf_solution: 0.136711[s]
char_and_sscanf_solution: 0.049708[s]
extractIntsSprintfTextScan: 0.042608[s]
all_loops: 0.017636[s]
eval_and_loops_solution: 0.099111[s]
Vous pouvez remarquer une différence dans la dernière étape, entre "Générant 10000..."et" Timing 1000000..."; afin de décimer la mémoire occupée (sinon, tout allait échouer sur la génération des cas de test), j'ai utilisé repmat(referee_test_case(1e4), 100, 1) au lieu de referee_test_case(1e6).
analyse comparative
peu de choses doivent être notées sur les codes de référence utilisés pour cette analyse comparative. C'est la même chose que les codes de référence de L'Amro avec ces changements -
- la division par
1000a été ajouté à toutes les solutions pour garder la cohérence entre les solutions. - la vérification de validité des erreurs est supprimée. Ça n'affectera pas les résultats de toute façon.
- la datasize (nombre de lignes) est étendue à
1000000et pour qui j'ai eu à garder le nombre de numéros dans chaque cellule8pour accueillir tout en mémoire. En outre, je pense que cela présenterait une comparaison équitable entre les solutions vectorisées et loopy. - les solutions basées sur mex sont évitées, mais j'aimerais voir des comparaisons d'exécution avec celles-ci aussi, si quelqu'un serait trop aimable d'inclure les solutions incluses dans ce de référence avec ceux mex.
- pour l'analyse comparative des codes GPU,
gputimeita été utilisé, à la place detimeit.
les codes sont empaquetés et disponibles ici. En elle, l'utiliser bench_script.m comme fonction principale.
Les Résultats De Benchmark
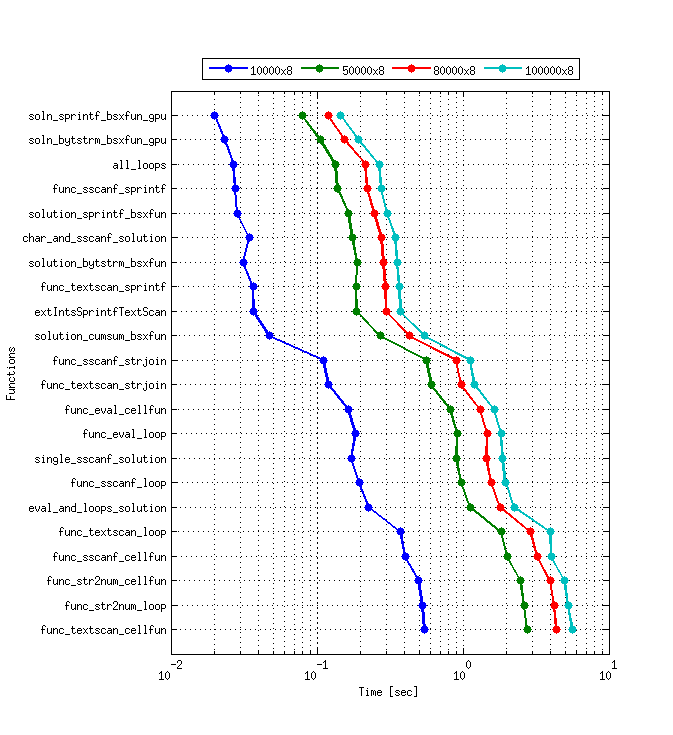
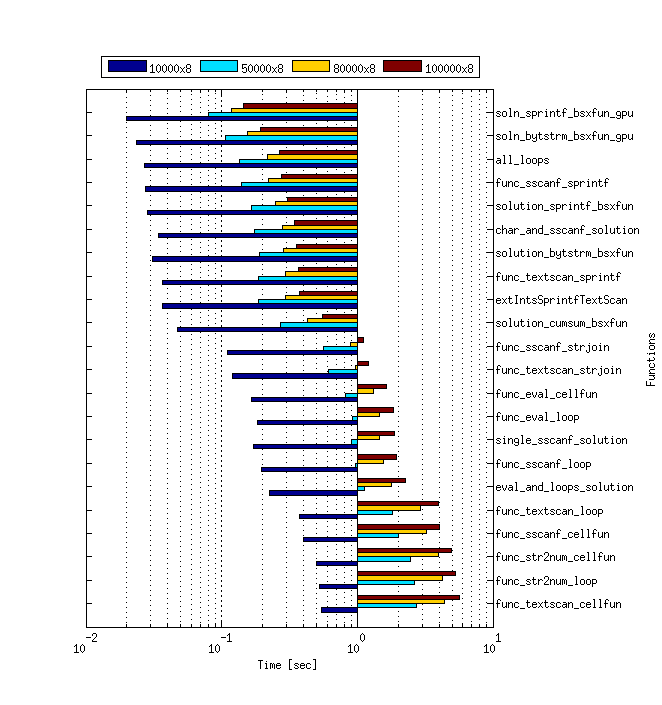
func nrows ncols time
__________________________ _____ _____ ________
'all_loops' 10000 8 0.026996
'char_and_sscanf_solution' 10000 8 0.034492
'eval_and_loops_solution' 10000 8 0.22548
'extIntsSprintfTextScan' 10000 8 0.036889
'func_eval_cellfun' 10000 8 0.16483
'func_eval_loop' 10000 8 0.1845
'func_sscanf_cellfun' 10000 8 0.40217
'func_sscanf_loop' 10000 8 0.19508
'func_sscanf_sprintf' 10000 8 0.027505
'func_sscanf_strjoin' 10000 8 0.11128
'func_str2num_cellfun' 10000 8 0.4976
'func_str2num_loop' 10000 8 0.5303
'func_textscan_cellfun' 10000 8 0.547
'func_textscan_loop' 10000 8 0.3752
'func_textscan_sprintf' 10000 8 0.036699
'func_textscan_strjoin' 10000 8 0.12059
'single_sscanf_solution' 10000 8 0.17122
'soln_bytstrm_bsxfun_gpu' 10000 8 0.023365
'soln_sprintf_bsxfun_gpu' 10000 8 0.019986
'solution_bytstrm_bsxfun' 10000 8 0.031165
'solution_cumsum_bsxfun' 10000 8 0.047445
'solution_sprintf_bsxfun' 10000 8 0.028417
'all_loops' 50000 8 0.13444
'char_and_sscanf_solution' 50000 8 0.1753
'eval_and_loops_solution' 50000 8 1.1242
'extIntsSprintfTextScan' 50000 8 0.1871
'func_eval_cellfun' 50000 8 0.82261
'func_eval_loop' 50000 8 0.91632
'func_sscanf_cellfun' 50000 8 2.0088
'func_sscanf_loop' 50000 8 0.97656
'func_sscanf_sprintf' 50000 8 0.13891
'func_sscanf_strjoin' 50000 8 0.56368
'func_str2num_cellfun' 50000 8 2.4786
'func_str2num_loop' 50000 8 2.6377
'func_textscan_cellfun' 50000 8 2.7452
'func_textscan_loop' 50000 8 1.8249
'func_textscan_sprintf' 50000 8 0.18556
'func_textscan_strjoin' 50000 8 0.60935
'single_sscanf_solution' 50000 8 0.90871
'soln_bytstrm_bsxfun_gpu' 50000 8 0.10591
'soln_sprintf_bsxfun_gpu' 50000 8 0.079611
'solution_bytstrm_bsxfun' 50000 8 0.18875
'solution_cumsum_bsxfun' 50000 8 0.27233
'solution_sprintf_bsxfun' 50000 8 0.16467
'all_loops' 80000 8 0.21602
'char_and_sscanf_solution' 80000 8 0.27855
'eval_and_loops_solution' 80000 8 1.7997
'extIntsSprintfTextScan' 80000 8 0.29733
'func_eval_cellfun' 80000 8 1.3171
'func_eval_loop' 80000 8 1.4647
'func_sscanf_cellfun' 80000 8 3.2232
'func_sscanf_loop' 80000 8 1.5664
'func_sscanf_sprintf' 80000 8 0.22136
'func_sscanf_strjoin' 80000 8 0.89605
'func_str2num_cellfun' 80000 8 3.9688
'func_str2num_loop' 80000 8 4.2199
'func_textscan_cellfun' 80000 8 4.3841
'func_textscan_loop' 80000 8 2.9181
'func_textscan_sprintf' 80000 8 0.29494
'func_textscan_strjoin' 80000 8 0.97383
'single_sscanf_solution' 80000 8 1.4542
'soln_bytstrm_bsxfun_gpu' 80000 8 0.15528
'soln_sprintf_bsxfun_gpu' 80000 8 0.11911
'solution_bytstrm_bsxfun' 80000 8 0.28552
'solution_cumsum_bsxfun' 80000 8 0.43238
'solution_sprintf_bsxfun' 80000 8 0.24801
'all_loops' 1e+05 8 0.26833
'char_and_sscanf_solution' 1e+05 8 0.34617
'eval_and_loops_solution' 1e+05 8 2.2465
'extIntsSprintfTextScan' 1e+05 8 0.37322
'func_eval_cellfun' 1e+05 8 1.641
'func_eval_loop' 1e+05 8 1.8339
'func_sscanf_cellfun' 1e+05 8 4.024
'func_sscanf_loop' 1e+05 8 1.9598
'func_sscanf_sprintf' 1e+05 8 0.27558
'func_sscanf_strjoin' 1e+05 8 1.1193
'func_str2num_cellfun' 1e+05 8 4.9592
'func_str2num_loop' 1e+05 8 5.2634
'func_textscan_cellfun' 1e+05 8 5.6636
'func_textscan_loop' 1e+05 8 3.981
'func_textscan_sprintf' 1e+05 8 0.36947
'func_textscan_strjoin' 1e+05 8 1.208
'single_sscanf_solution' 1e+05 8 1.8665
'soln_bytstrm_bsxfun_gpu' 1e+05 8 0.19389
'soln_sprintf_bsxfun_gpu' 1e+05 8 0.14588
'solution_bytstrm_bsxfun' 1e+05 8 0.35404
'solution_cumsum_bsxfun' 1e+05 8 0.54906
'solution_sprintf_bsxfun' 1e+05 8 0.30324
Configuration Du Système
MATLAB Version: 8.3.0.532 (R2014a)
Operating System: Ubuntu 14.04 LTS 64-bit
RAM: 4GB
CPU Model: Intel® Pentium® Processor E5400 (2M Cache, 2.70 GHz)
GPU Model: GTX 750Ti 2GB
configinfo.m sortie (important) -
MATLAB accelerator enabled
MATLAB JIT: enabled
MATLAB assertions: disabled
MATLAB Desktop: enabled
Java JVM: enabled
CPU: x86 Family 6 Model 23 Stepping 10, GenuineIntel
Number of processors: 2
CPU speed is: 2700 MHz
RAM: 4046992 kB
Swap space: 9760764 kB
Number of cores: 2
Number of threads: 2
ici, dans L'esprit de MATLAB holiday, il y a une solution hautement vectorisée:
function M = func_voigt_loop(C)
S = sprintf('_%s', C{:});
digitpos = [find(S(2:end) == '_'), numel(S)];
M = zeros(size(digitpos));
place = 1;
while 1
digits = S(digitpos);
mask = double(digits ~= '_');
M = M + mask.*(digits - '0') * place;
place = place * 10;
digitpos = digitpos - mask;
if ~any(mask); break; end
end
M = reshape(M, [], numel(C))';
end
il ne s'agit que de quelques lignes, faciles à comprendre (saisir le chiffre de chaque nombre, ajouter le chiffre des dizaines, etc), et n'utilise pas de fonctions "exotiques" comme eval ou textscan. Il est aussi très vite.
C'est une idée similaire à quelque chose que j'ai développé précédemment pour le faire datenum sur une colonne entière de données dans un fichier CSV, la version MATLAB, même avec un motif particulier spécifié, c'était juste horriblement lent. Une version ultérieure de MATLAB a amélioré datenum de manière significative, mais ma version à la main bat toujours handily.