Optimisation MATLAB de L'Orthogonalisation Gram-Schmidt pondérée
j'ai une fonction dans MATLAB qui effectue l' Gram-Schmidt Orthogonalisation avec une pondération très importante appliquée aux produits intérieurs (Je ne pense pas que la fonction intégrée de MATLAB supporte cela). Cette fonction fonctionne aussi bien que je peux dire, cependant, il est trop lent sur les grandes matrices. Quelle serait la meilleure façon d'améliorer cela?
j'ai essayé de convertir en fichier MEX mais j'ai perdu la parallélisation avec le compilateur que j'utilise et c'est alors plus lent.
je pensais l'exécuter sur un GPU car les multiplications par éléments sont très parallèles. (Mais je préfère la mise en œuvre afin d'être facilement portable)
est-ce que quelqu'un peut vectoriser ce code ou le rendre plus rapide? Je ne suis pas sûr de la façon de le faire avec élégance ...
je sais que le stackoverflow esprits ici sont incroyables, c'est le défi :)
Function
function [Q, R] = Gram_Schmidt(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
v = zeros(n, 1);
for j = 1:n
v = A(:,j);
for i = 1:j-1
R(i,j) = sum( v .* conj( Q(:,i) ) .* w ) / ...
sum( Q(:,i) .* conj( Q(:,i) ) .* w );
v = v - R(i,j) * Q(:,i);
end
R(j,j) = norm(v);
Q(:,j) = v / R(j,j);
end
end
où A est un m x n matrice de nombres complexes et w est un m x 1 vecteur des nombres réels.
goulot
C'est l'expression de R(i,j) qui est la partie la plus lente de la fonction (pas sûr à 100% si la notation est correct):
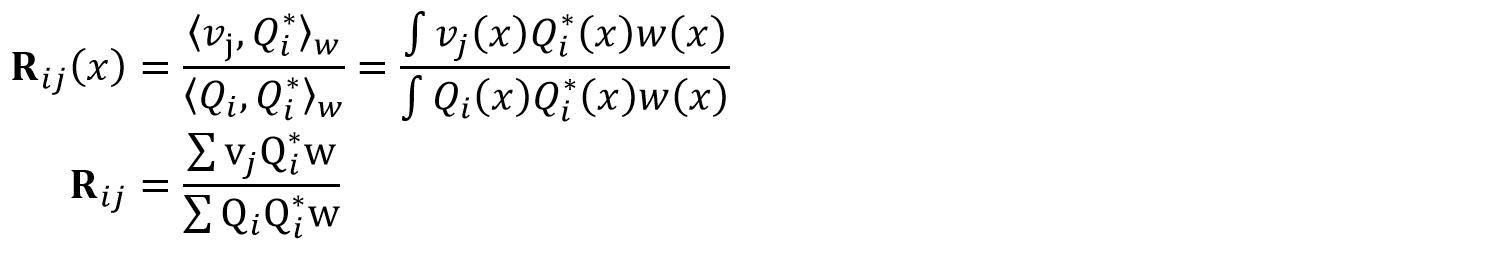
où w est une fonction de poids non négative.
Le produit intérieur pondéré est mentionné sur plusieurs pages de Wikipedia,c'est la fonction de poids et c'est un sur les fonctions orthogonales.
Reproduction
vous pouvez produire des résultats en utilisant le script suivant:
A = complex( rand(360000,100), rand(360000,100));
w = rand(360000, 1);
[Q, R] = Gram_Schmidt(A, w);
où A et w sont les entrées.
vitesse et calcul
Si vous utilisez le script ci-dessus, vous obtiendrez des résultats du profileur synonyme à la suivante:
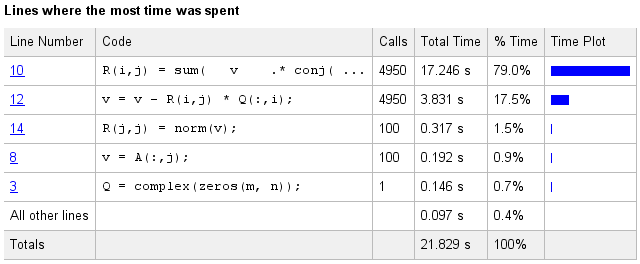
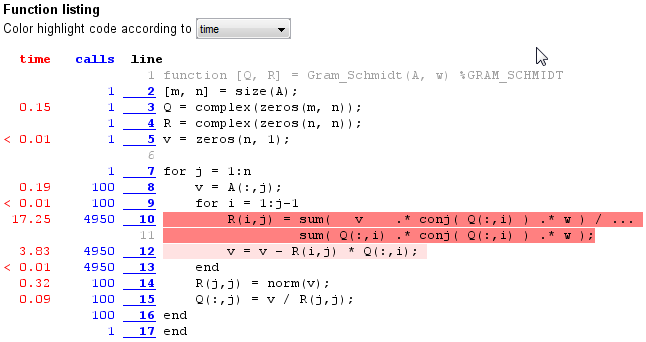
Essais Résultat
vous pouvez tester les résultats en comparant une fonction avec celle ci-dessus en utilisant le script suivant:
A = complex( rand( 100, 10), rand( 100, 10));
w = rand( 100, 1);
[Q , R ] = Gram_Schmidt( A, w);
[Q2, R2] = Gram_Schmidt2( A, w);
zeros1 = norm( Q - Q2 );
zeros2 = norm( R - R2 );
où Gram_Schmidt est la fonction décrite précédemment et Gram_Schmidt2 est une autre fonction. Les résultats zeros1 et zeros2 devrait alors être très proche de zéro.
Remarque:
j'ai essayé d'accélérer le calcul de R(i,j) avec ce qui suit mais en vain ...
R(i,j) = ( w' * ( v .* conj( Q(:,i) ) ) ) / ...
( w' * ( Q(:,i) .* conj( Q(:,i) ) ) );
3 réponses
1)
Ma première tentative de vectorisation:
function [Q, R] = Gram_Schmidt1(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
for j = 1:n
v = A(:,j);
QQ = Q(:,1:j-1);
QQ = bsxfun(@rdivide, bsxfun(@times, w, conj(QQ)), w.' * abs(QQ).^2);
for i = 1:j-1
R(i,j) = (v.' * QQ(:,i));
v = v - R(i,j) * Q(:,i);
end
R(j,j) = norm(v);
Q(:,j) = v / R(j,j);
end
end
malheureusement, il s'est avéré être plus lent que la fonction originale.
2)
Puis j'ai réalisé que les colonnes de cette matrice intermédiaire QQ sont construits progressivement, et que les précédents ne sont pas modifiés. Voici donc ma deuxième tentative:
function [Q, R] = Gram_Schmidt2(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
QQ = complex(zeros(m, n-1));
for j = 1:n
if j>1
qj = Q(:,j-1);
QQ(:,j-1) = (conj(qj) .* w) ./ (w.' * (qj.*conj(qj)));
end
v = A(:,j);
for i = 1:j-1
R(i,j) = (v.' * QQ(:,i));
v = v - R(i,j) * Q(:,i);
end
R(j,j) = norm(v);
Q(:,j) = v / R(j,j);
end
end
techniquement, aucune vectorisation majeure n'a été faite; je n'ai que précalculé les résultats intermédiaires, et déplacé le calcul de l'extérieur de la boucle interne.
basée sur un benchmark rapide, cette nouvelle version est certainement plus rapide:
% some random data
>> M = 10000; N = 100;
>> A = complex(rand(M,N), rand(M,N));
>> w = rand(M,1);
% time
>> timeit(@() Gram_Schmidt(A,w), 2) % original version
ans =
1.2444
>> timeit(@() Gram_Schmidt1(A,w), 2) % first attempt (vectorized)
ans =
2.0990
>> timeit(@() Gram_Schmidt2(A,w), 2) % final version
ans =
0.4698
% check results
>> [Q,R] = Gram_Schmidt(A,w);
>> [Q2,R2] = Gram_Schmidt2(A,w);
>> norm(Q-Q2)
ans =
4.2796e-14
>> norm(R-R2)
ans =
1.7782e-12
EDIT:
suivant les commentaires, nous pouvons réécrire la deuxième solution pour se débarrasser du SI-statmenet, en déplaçant cette partie à la fin de la boucle externe (I. e immédiatement après le calcul de la nouvelle colonne Q(:,j), nous calculons et stockons les données correspondantes QQ(:,j)).
la fonction est identique en sortie, et le timing n'est pas si différent non plus; le code est juste un peu plus court!
function [Q, R] = Gram_Schmidt3(A, w)
[m, n] = size(A);
Q = zeros(m, n, 'like',A);
R = zeros(n, n, 'like',A);
QQ = zeros(m, n, 'like',A);
for j = 1:n
v = A(:,j);
for i = 1:j-1
R(i,j) = (v.' * QQ(:,i));
v = v - R(i,j) * Q(:,i);
end
R(j,j) = norm(v);
Q(:,j) = v / R(j,j);
QQ(:,j) = (conj(Q(:,j)) .* w) ./ (w.' * (Q(:,j).*conj(Q(:,j))));
end
end
notez que j'ai utilisé le zeros(..., 'like',A) syntaxe (nouvelle dans les versions récentes de MATLAB). Cela nous permet d'exécuter la fonction non modifiée sur le GPU (en supposant que vous avez la boîte à outils du calcul parallèle):
% CPU
[Q3,R3] = Gram_Schmidt3(A, w);
vs.
% GPU
AA = gpuArray(A);
[Q3,R3] = Gram_Schmidt3(AA, w);
malheureusement dans mon cas, ce n'était pas plus rapide. En fait, il était beaucoup plus lent à courir sur le GPU que le CPU, mais il a été vaut le coup :)
Il y a une longue discussion ici, mais, pour accéder à la réponse. Vous avez pondéré le numérateur et le dénominateur du calcul R par un vecteur W. La pondération a lieu sur la boucle intérieure et consiste en un produit à trois points, un point Q point w dans le numérateur et un point Q point w dans le dénominateur. Si vous faites une modification, je pense que le code sera exécuté beaucoup plus rapidement. Écrire num = (un point sqrt (w)) point(Q point sqrt (w)) et écrire den = (Q point sqrt (w)) point(Q point sqrt (w)). Qui se déplace de l' (Un point sqrt (w)) et(Q point sqrt (w)) de la boucle interne.
je voudrais donner une description de la formulation à L'Orthogonalisation Gram Schmidt, qui, si tout va bien, en plus de donner une solution de calcul alternative, donne plus de détails sur l'avantage de GSO.
les "buts" de L'OSG sont doubles. Tout d'abord, pour permettre la solution d'une équation comme Ax=y, Où A a beaucoup plus de lignes que de colonnes. Cette situation se produit fréquemment lors de la mesure de données, en ce qu'il est facile de mesurer plus de données que le nombre d'États. L'approche du premier objectif est de réécrire a comme QR de façon à ce que les colonnes de Q soient orthogonales et normalisées, et R soit une matrice triangulaire. L'algorithme que vous avez fourni, je crois, atteint le premier objectif. Le Q représente L'espace de base de la matrice A, et R représente l'amplitude de chaque espace de base nécessaire pour générer chaque colonne de A.
le deuxième but de L'osg est de classer vecteurs de base, par ordre d'importance. Ce le pas que vous ne l'avez pas fait. Et, tout en incluant cette étape, peut augmenter le temps de solution, les résultats détermineront quels éléments de x sont importants, selon les données contenues dans les mesures représentées par A.
mais, je pense, avec cette implémentation, la solution est plus rapide que l'approche que vous avez présentée.
Aij = QIJ Rij où Qj est orthonormal et Rij est triangulaire supérieur, Ri, j>i = 0. Qj sont les Vecteurs de base orthogonaux pour A, et Rij est la participation de chaque Qj pour créer une colonne dans A. So,
A_j1 = Q_j1 * R_1,1
A_j2 = Q_j1 * R_1,2 + Q_j2 * R_2,2
A_j3 = Q_j1 * R_1,3 + Q_j2 * R_2,3 + Q_j3 * R_3,3
par inspection, vous pouvez écrire
A_j1 = ( A_j1 / | A_j1 | ) * | A_j1 | = Q_j1 * R_1,1
ensuite vous projetez Q_j1 sur toutes les autres colonnes A pour obtenir les éléments R_1,j
R_1,2 = Q_j1 dot Aj2
R_1,3 = Q_j1 dot Aj3
...
R_1,j(j>1) = A_j dot Q_j1
puis vous soustrayez les éléments du projet de Q_j1 des colonnes de A (Cela placerait la première colonne à zéro, de sorte que vous pouvez ignorer la première colonne
for j = 2,n
A_j = A_j - R_1,j * Q_j1
end
maintenant une colonne d'un a été supprimé, le premier vecteur de base orthonormal,Q, j1, a été déterminé, et la contribution du premier vecteur de base à chaque colonne,R_1, j a été déterminée, et la contribution du premier vecteur de base a été soustraite de chaque colonne. Répétez ce processus pour les colonnes restantes de A pour obtenir les colonnes restantes de Q et les lignes de R.
for i = 1,n
R_ii = |A_i| A_i is the ith column of A, |A_i| is magnitude of A_i
Q_i = A_i / R_ii Q_i is the ith column of Q
for j = i, n
R_ij = | A_j dot Q_i |
A_j = A_j - R_ij * Q_i
end
end
vous essayez de peser les rangs de A, avec w. Voici une approche. Je serait de normaliser w, et d'intégrer les vous avez "enlevé" les effets de w en multipliant et en divisant par W. Une alternative à "supprimer" l'effet est de normaliser l'amplitude de w à un.
w = w / | w |
for i = 1,n
R_ii = |A_i inner product w| # A_i inner product w = A_i .* w
Q_i = A_i / R_ii
for j = i, n
R_ij = | (A_i inner product w) dot Q_i | # A dot B = A' * B
A_j = A_j - R_ij * Q_i
end
end
une autre approche de mise en oeuvre de w consiste à normaliser w et ensuite prémultipliquer chaque colonne de A par W. Qui pèse proprement les rangs de A, et réduit le nombre de multiplications.
utiliser ce qui suit peut aider à accélérer votre code
A inner product B = A .* B
A dot w = A' w
(A B)' = B'A'
A' conj(A) = |A|^2
ce qui précède peut être vectorisé facilement dans matlab, à peu près comme écrit.
mais, il vous manque la deuxième partie du classement de A, qui vous dit quels états (éléments de x dans A x = y) sont représentés de manière significative dans les données
la procédure de classement est facile à décrire, mais je vous laisse travailler sur les détails de programmation. La procédure ci-dessus suppose essentiellement les colonnes de A sont dans l'ordre de signification, et la première colonne est soustraite de toutes les autres colonnes, puis le 2ème la colonne est soustraite des autres colonnes, etc. La première rangée de R représente la contribution de la première colonne de Q à chaque colonne de A. Si vous additionnez la valeur absolue de la première rangée de R contributions, vous obtenez une mesure de la contribution de la première colonne de Q à la matrice A. Donc, vous évaluez juste chaque colonne de A comme la première (ou la prochaine) colonne de Q, et de déterminer le score de classement de la contribution de cette colonne de Q aux autres colonnes de A. Ensuite, sélectionnez le A colonne qui a le rang le plus élevé comme colonne Q suivante. Le codage se résume essentiellement à la pré-estimation de la rangée suivante de R, pour chaque colonne restante en A, afin de déterminer quelle magnitude de R A la plus grande amplitude. Avoir un vecteur d'index qui représente l'ordre original de colonne de A sera bénéfique. En classant les vecteurs de base, vous vous retrouvez avec les vecteurs de base" principaux " qui représentent A, qui est généralement beaucoup plus petit en nombre que le nombre de colonnes dans A.
en outre, si vous classez les colonnes, il n'est pas nécessaire de calculer chaque colonne de R. Lorsque vous savez quelles colonnes de A ne contiennent pas de renseignements utiles, il n'y a pas d'avantage réel à conserver ces colonnes.
dans la dynamique structurale, une approche pour réduire le nombre de degrés de liberté est de calculer les valeurs propres, en supposant que vous avez des valeurs représentatives pour la matrice de masse et de rigidité. Si vous y réfléchissez, l'approche ci-dessus peut être utilisée pour "calculer "les matrices M et K (et C) à partir de la réponse mesurée, et aussi identifier les" formes de réponse de mesure " qui sont représentées de façon significative dans les données. Ces sont différentes, et potentiellement plus importante que les formes de mode. Ainsi, vous pouvez résoudre des problèmes très difficiles, i.e., estimation des matrices d'état et le nombre de degrés de liberté représentés, à partir de la réponse mesurée, par l'approche ci-dessus. Si vous lisez sur N4SID, il a fait quelque chose de similaire, sauf QU'il a utilisé SVD au lieu de GSO. Je n'aime pas la description technique pour N4SID, trop d'attention sur la notation de la projection vectorielle, qui est simplement un produit de point.
il peut y avoir une ou deux erreurs dans les informations ci-dessus, j'écris ceci du haut de ma tête, avant de me précipiter au travail. Ainsi, vérifiez l'algorithme / équations que vous mettez en œuvre... Bonne Chance
pour en revenir à votre question, sur la façon d'optimiser l'algorithme lorsque vous pondérez avec w. Voici un algorithme GSO de base, sans tri, écrit compatible avec votre fonction.
notez que le code ci-dessous est en octave, pas en matlab. Il ya quelques différences mineures.
function [Q, R] = Gram_Schmidt_2(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
# Outer loop identifies the basis vectors
for j = 1:n
aCol = A(:,j);
# Subtract off the basis vector
for i = 1:(j-1)
R(i,j) = ctranspose(Q(:,j)) * aCol;
aCol = aCol - R(i,j) * Q(:,j);
end
amp_A_col = norm(aCol);
R(j,j) = amp_A_col;
Q(:,j) = aCol / amp_A_col;
end
end
pour obtenir votre algorithme, ne changez qu'une ligne. Mais vous perdez beaucoup de vitesse car "ctranspose(Q(:,j)) * aCol" est une opération vectorielle mais "sum( aCol .* conj (Q (:, i) ) .* w )" est une opération de ligne.
function [Q, R] = Gram_Schmidt_2(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
# Outer loop identifies the basis vectors
for j = 1:n
aCol = A(:,j);
# Subtract off the basis vector
for i = 1:(j-1)
# R(i,j) = ctranspose(Q(:,j)) * aCol;
R(i,j) = sum( aCol .* conj( Q(:,i) ) .* w ) / ...
sum( Q(:,i) .* conj( Q(:,i) ) .* w );
aCol = aCol - R(i,j) * Q(:,j);
end
amp_A_col = norm(aCol);
R(j,j) = amp_A_col;
Q(:,j) = aCol / amp_A_col;
end
end
vous pouvez le changer de nouveau à une opération vectorielle en pondérant aCol et Q par le sqrt de w.
function [Q, R] = Gram_Schmidt_3(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
Q_sw = complex(zeros(m, n));
sw = w .^ 0.5;
for j = 1:n
aCol = A(:,j);
aCol_sw = aCol .* sw;
# Subtract off the basis vector
for i = 1:(j-1)
# R(i,j) = ctranspose(Q(:,i)) * aCol;
numTerm = ctranspose( Q_sw(:,i) ) * aCol_sw;
denTerm = ctranspose( Q_sw(:,i) ) * Q_sw(:,i);
R(i,j) = numTerm / denTerm;
aCol_sw = aCol_sw - R(i,j) * Q_sw(:,i);
end
aCol = aCol_sw ./ sw;
amp_A_col = norm(aCol);
R(j,j) = amp_A_col;
Q(:,j) = aCol / amp_A_col;
Q_sw(:,j) = Q(:,j) .* sw;
end
end
comme le souligne JacobD, la fonction ci-dessus ne court pas plus vite. Il est possible qu'il faille du temps pour créer les tableaux supplémentaires. Une autre stratégie de regroupement pour le produit triple est de grouper w avec conj(Q). Espérons que cela soit plus rapide...
function [Q, R] = Gram_Schmidt_4(A, w)
[m, n] = size(A);
Q = complex(zeros(m, n));
R = complex(zeros(n, n));
for j = 1:n
aCol = A(:,j);
for i = 1:(j-1)
cqw = conj(Q(:,i)) .* w;
R(i,j) = ( transpose( aCol ) * cqw) ...
/ (transpose( Q(:,i) ) * cqw);
aCol = aCol - R(i,j) * Q(:,i);
end
amp_A_col = norm(aCol);
R(j,j) = amp_A_col;
Q(:,j) = aCol / amp_A_col;
end
end
Voici une fonction de pilote pour chronométrer les différentes versions.
function Gram_Schmidt_tester_2
nSamples = 360000;
nMeas = 100;
nMeas = 15;
A = complex( rand(nSamples,nMeas), rand(nSamples,nMeas));
w = rand(nSamples, 1);
profile on;
[Q1, R1] = Gram_Schmidt_basic(A);
profile off;
data1 = profile ("info");
tData1=data1.FunctionTable(1).TotalTime;
approx_zero1 = A - Q1 * R1;
max_value1 = max(max(abs(approx_zero1)));
profile on;
[Q2, R2] = Gram_Schmidt_w_Orig(A, w);
profile off;
data2 = profile ("info");
tData2=data2.FunctionTable(1).TotalTime;
approx_zero2 = A - Q2 * R2;
max_value2 = max(max(abs(approx_zero2)));
sw=w.^0.5;
profile on;
[Q3, R3] = Gram_Schmidt_sqrt_w(A, w);
profile off;
data3 = profile ("info");
tData3=data3.FunctionTable(1).TotalTime;
approx_zero3 = A - Q3 * R3;
max_value3 = max(max(abs(approx_zero3)));
profile on;
[Q4, R4] = Gram_Schmidt_4(A, w);
profile off;
data4 = profile ("info");
tData4=data4.FunctionTable(1).TotalTime;
approx_zero4 = A - Q4 * R4;
max_value4 = max(max(abs(approx_zero4)));
profile on;
[Q5, R5] = Gram_Schmidt_5(A, w);
profile off;
data5 = profile ("info");
tData5=data5.FunctionTable(1).TotalTime;
approx_zero5 = A - Q5 * R5;
max_value5 = max(max(abs(approx_zero5)));
profile on;
[Q2a, R2a] = Gram_Schmidt2a(A, w);
profile off;
data2a = profile ("info");
tData2a=data2a.FunctionTable(1).TotalTime;
approx_zero2a = A - Q2a * R2a;
max_value2a = max(max(abs(approx_zero2a)));
profshow (data1, 6);
profshow (data2, 6);
profshow (data3, 6);
profshow (data4, 6);
profshow (data5, 6);
profshow (data2a, 6);
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data1.FunctionTable(1).FunctionName,
data1.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value1)
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data2.FunctionTable(1).FunctionName,
data2.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value2)
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data3.FunctionTable(1).FunctionName,
data3.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value3)
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data4.FunctionTable(1).FunctionName,
data4.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value4)
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data5.FunctionTable(1).FunctionName,
data5.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value5)
sprintf('Time for %s is %5.3f sec with %d samples and %d meas, max value is %g',
data2a.FunctionTable(1).FunctionName,
data2a.FunctionTable(1).TotalTime,
nSamples, nMeas, max_value2a)
end
sur mon vieil ordinateur portable, en Octave, les résultats sont
ans = Time for Gram_Schmidt_basic is 0.889 sec with 360000 samples and 15 meas, max value is 1.57009e-16
ans = Time for Gram_Schmidt_w_Orig is 0.952 sec with 360000 samples and 15 meas, max value is 6.36717e-16
ans = Time for Gram_Schmidt_sqrt_w is 0.390 sec with 360000 samples and 15 meas, max value is 6.47366e-16
ans = Time for Gram_Schmidt_4 is 0.452 sec with 360000 samples and 15 meas, max value is 6.47366e-16
ans = Time for Gram_Schmidt_5 is 2.636 sec with 360000 samples and 15 meas, max value is 6.47366e-16
ans = Time for Gram_Schmidt2a is 0.905 sec with 360000 samples and 15 meas, max value is 6.68443e-16
Ces résultats indiquent l'algorithme le plus rapide est-ce que l'algorithme sqrt_w ci-dessus est à 0.39 sec, suivi du regroupement de conj(Q) avec w (ci-dessus) à 0.452 sec, puis la version 2 de la solution Amro à 0.905 sec, puis l'algorithme original dans la question à 0.952 sec, puis une version 5 qui échange lignes / colonnes pour voir si le stockage en ligne présenté (code non inclus) à 2.636 sec. Ces résultats indiquent que la séparation de sqrt(w) entre A et Q est la solution la plus rapide. Mais ces résultats ne sont pas compatibles avec le commentaire de JacobD sur sqrt (w) n'étant pas plus rapide.
Il est possible de vectoriser ce donc, une seule boucle est nécessaire. Le changement fondamental important par rapport à l'algorithme original est que si vous changez les boucles intérieure et extérieure, vous pouvez vectoriser la projection du vecteur de référence à tous les vecteurs restants. De travail @Amro's solution, j'ai trouvé qu'une boucle interne est effectivement plus rapide que la matrice de la soustraction. Je ne comprends pas pourquoi ce serait. Chronométrer ceci contre @Amro's solution, elle est d'environ 45% plus rapide.
function [Q, R] = Gram_Schmidt5(A, w)
Q = A;
n_dimensions = size(A, 2);
R = zeros(n_dimensions);
R(1, 1) = norm(Q(:, 1));
Q(:, 1) = Q(:, 1) ./ R(1, 1);
for i = 2 : n_dimensions
Qw = (Q(:, i - 1) .* w)' * Q(:, (i - 1) : end);
R(i - 1, i : end) = Qw(2:end) / Qw(1);
%% Surprisingly this loop beats the matrix multiply
for j = i : n_dimensions
Q(:, j) = Q(:, j) - Q(:, i - 1) * R(i - 1, j);
end
%% This multiply is slower than above
% Q(:, i : end) = ...
% Q(:, i : end) - ...
% Q(:, i - 1) * R(i - 1, i : end);
R(i, i) = norm(Q(:,i));
Q(:, i) = Q(:, i) ./ R(i, i);
end