Élément majoritaire-parties d'un tableau

o (log n) requêtes et O (N log n) prétraitement/espace pourrait être obtenue en trouvant et en utilisant majority intervals avec les propriétés suivantes:

1. pour chaque valeur il peut y avoir un ou plusieurs intervalles de Majorité (ou il peut n'y en avoir aucun si les éléments avec ces valeurs sont trop clairsemés; nous n'avons pas besoin de intervalles de Majorité de longueur 1 parce qu'ils peuvent être utiles seulement pour des intervalles de requête de taille 1 qui sont mieux traités comme un cas spécial).
2. si l'intervalle de requête se trouve complètement à l'intérieur de l'un de ces intervalles de Majorité , correspondant valeur peut être l'élément de majorité de cet intervalle de requête.
3. S'il n'y a pas de majority interval completely contain query interval, correspondant valeur ne peut pas être l'élément majoritaire de cet intervalle de requête.
4. chaque élément du tableau d'entrée est couvert par O(log n) majority intervals .

en d'autres termes, le seul but de majority intervals est de fournir des candidats d'éléments majoritaires O(log n) Pour n'importe quel intervalle d'interrogation.

This l'algorithme utilise structures de données :

1. liste des positions pour chaque valeur du tableau d'entrée ( map<Value, vector<Position>> ). Il est également possible d'utiliser unordered_map pour améliorer les performances (mais nous aurons besoin d'extraire toutes les clés et de les Trier pour que la structure #3 soit remplie dans l'ordre approprié).
2. liste des majority intervals pour chaque valeur ( vector<Interval> ).
3. structure de Données pour le traitement des requêtes ( vector<small_map<Value, Data>> ). Où Data contient deux indices du vecteur approprié de la structure #1 pointant vers la position suivante/précédente des éléments avec valeur . mise à Jour: Grâce à @justhalf, il est préférable de les stocker dans Data des fréquences cumulées des éléments avec le valeur . small_map peut être mis en œuvre comme vecteur trié de paires - prétraitement ajoutera des éléments déjà dans l'ordre trié et la requête utilisera small_map seulement pour la recherche linéaire.

prétraitement:

1. balayer le tableau d'entrées et pousser la position du courant au vecteur approprié dans la structure #1.
2. effectuer les étapes 3 .. 4 pour chaque vecteur de la structure #1.
3. Transformer une liste de positions dans la liste de majority intervals . Voir les détails ci-dessous.
4. pour chaque indice du tableau d'entrées couvert par l'un des majority intervals , insérer les données à l'élément approprié de la structure #3: valeur et les positions des éléments précédents/suivants avec cette valeur (ou fréquence cumulative de cette valeur ).

Requête:

1. si la longueur de l'intervalle d'interrogation est 1, retourner l'élément correspondant du tableau source.
2. pour le point de départ de l'intervalle d'interrogation, récupérez l'élément correspondant du vecteur de la 3ème structure. Pour chaque élément de la carte effectuer l'étape 3. Numérisez tous les éléments de la carte correspondant au point final de l'intervalle de requête en parallèle avec cette carte pour permettre à O(1) la complexité de l'étape 3 (au lieu de O(log n)).
3. si la carte correspondant au point final de l'intervalle d'interrogation contient la correspondance valeur , calculer s3[stop][value].prev - s3[start][value].next + 1 . Si elle est supérieure à la moitié de l'intervalle de requête, retourner valeur . Si les fréquences cumulatives sont utilisées à la place des index suivants/précédents, calculer s3[stop+1][value].freq - s3[start][value].freq à la place.
4. si rien n'est trouvé à l'étape 3, retournez "rien".

partie principale l'algorithme obtient majority intervals de la liste des positions:

1. attribuer poids à chaque position dans la liste: number_of_matching_values_to_the_left - number_of_nonmatching_values_to_the_left .
2. Filtre seulement poids dans l'ordre décroissant strictement (greedily) au tableau" prefix": for (auto x: positions) if (x < prefix.back()) prefix.push_back(x); .
3. Filtre seulement poids dans un ordre strictement croissant (greedily, à l'envers) pour le "suffixe" tableau: reverse(positions); for (auto x: positions) if (x > suffix.back()) suffix.push_back(x); .
4. Scan "préfixe" et du suffixe" tableaux et de trouver des intervalles de tous les "préfixe" élément à la place correspondante dans le "suffixe" tableau et de tous les "suffixe" élément à la place correspondante dans le "préfixe" array. (Si le poids de tous les éléments de "suffixe "est inférieur à celui de l'élément de" préfixe "ou si leur position n'est pas à sa droite, aucun intervalle n'est généré; s'il n'y a pas d'élément de" suffixe " ayant exactement le poids de l'élément de "préfixe" donné." élément, obtenir le plus proche "suffixe" élément avec un poids plus grand et étendre l'intervalle avec cette différence de poids à droite).
5. fusionnent des intervalles se chevauchant.

propriétés 1 .. 3 pour la majorité des intervalles sont garantis par cet algorithme. Quant à la propriété #4, la seule façon que je pouvais imaginer de couvrir un élément avec un nombre maximum de majority intervals est comme ceci: 11111111222233455666677777777 . Ici l'élément 4 est couvert par 2 * log n intervalles, donc cette propriété semble satisfaite. Voir plus de preuve formelle de cette propriété à la fin de ce post.

exemple:

pour le tableau d'entrée"0 1 2 0 0 1 1 0" les listes de postes suivantes seraient produites:

value  positions
    0  0 3 4 7
    1  1 5 6
    2  2

Positions pour valeur 0 aura les propriétés suivantes:

weights:    0:1 3:0 4:1 7:0
prefix:     0:1 3:0          (strictly decreasing)
suffix:     4:1 7:0          (strictly increasing when scanning backwards)
intervals:  0->4 3->7 4->0 7->3
merged intervals: 0-7

Positions pour valeur 1 aura les propriétés suivantes:

weights:    1:0  5:-2  6:-1
prefix:     1:0  5:-2
suffix:     1:0  6:-1
intervals:  1->none 5->6+1 6->5-1 1->none
merged intervals: 4-7

"1519340920 de la Requête" structure de données:

positions value next prev
        0     0    0    x
     1..2     0    1    0
        3     0    1    1
        4     0    2    2
        4     1    1    x
        5     0    3    2
    ...

"1519340920 de la Requête" [0,4]:

prev[4][0]-next[0][0]+1=2-0+1=3
query size=5
3>2.5, returned result 0

"1519340920 de la Requête" [2,5]:

prev[5][0]-next[2][0]+1=2-1+1=2
query size=4
2=2, returned result "none"

noter qu'il n'y a aucune tentative d'inspecter l'élément "1" parce que son intervalle de la majorité ne comprend aucun de ces intervalles.

preuve de propriété #4:

la Majorité des intervalles sont construits de telle manière que strictement plus de 1/3 de l'ensemble de leurs éléments correspondants valeur . Ce rapport est le plus proche de 1/3 pour les sous-tableaux comme any*(m-1) value*m any*m , par exemple, 01234444456789 .

pour rendre cette preuve plus évidente, nous pourrions représenter chaque intervalle comme un point en 2D: chaque point de départ possible représenté par un axe horizontal et chaque point final possible représenté par un axe vertical (voir schéma ci-dessous).

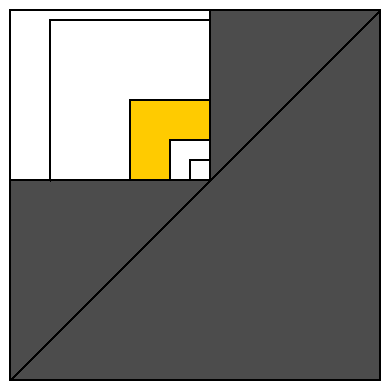
tous les intervalles valides sont situés sur ou au-dessus de la diagonale. Le rectangle blanc représente tous les intervalles couvrant un élément de tableau (représenté comme l'intervalle de taille de l'unité sur son coin inférieur droit).

couvrons ce rectangle blanc avec des carrés de taille 1, 2, 4, 8, 16, ... partager le même coin inférieur droit. Cela divise la zone blanche en zones O(log n) semblables à la zone jaune (et un seul carré de taille 1 contenant un seul intervalle de taille 1 qui est ignoré par cet algorithme).

combien majority intervals peut être placé dans la zone jaune. Un intervalle (situé au coin le plus proche de la diagonale) occupe 1/4 des éléments appartenant à l'intervalle au coin le plus éloigné de la diagonale (et ce plus grand intervalle contient tous les éléments appartenant à un intervalle dans la zone jaune). Cela signifie que le plus petit intervalle contient strictement plus de 1/12 valeurs disponibles pour toute la zone jaune. Donc, si nous essayons de placer 12 intervalles à la zone jaune, nous n'avons pas assez d'éléments pour différentes valeurs . Ainsi la zone jaune ne peut pas contenir plus de 11 majority intervals . Et le rectangle blanc ne peut pas contenir plus de 11 * log n la majorité des intervalles . La preuve terminé.

11 * log n est une surestimation. Comme je l'ai dit plus tôt, il est difficile d'imaginer plus de 2 * log n majority intervals couvrant un élément. Et même cette valeur est beaucoup plus grande que le nombre moyen de couvrant intervalles de la majorité .

C++11 mise en œuvre. Voir il soit à ideone ou ici:

#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <random>

constexpr int SrcSize = 1000000;
constexpr int NQueries = 100000;

using src_vec_t = std::vector<int>;
using index_vec_t = std::vector<int>;
using weight_vec_t = std::vector<int>;
using pair_vec_t = std::vector<std::pair<int, int>>;
using index_map_t = std::map<int, index_vec_t>;
using interval_t = std::pair<int, int>;
using interval_vec_t = std::vector<interval_t>;
using small_map_t = std::vector<std::pair<int, int>>;
using query_vec_t = std::vector<small_map_t>;

constexpr int None = -1;
constexpr int Junk = -2;

src_vec_t generate_e()
{ // good query length = 3
    src_vec_t src;
    std::random_device rd;
    std::default_random_engine eng{rd()};
    auto exp = std::bind(std::exponential_distribution<>{0.4}, eng);

    for (int i = 0; i < SrcSize; ++i)
    {
        int x = exp();
        src.push_back(x);
        //std::cout << x << ' ';
    }

    return src;
}

src_vec_t generate_ep()
{ // good query length = 500
    src_vec_t src;
    std::random_device rd;
    std::default_random_engine eng{rd()};
    auto exp = std::bind(std::exponential_distribution<>{0.4}, eng);
    auto poisson = std::bind(std::poisson_distribution<int>{100}, eng);

    while (int(src.size()) < SrcSize)
    {
        int x = exp();
        int n = poisson();

        for (int i = 0; i < n; ++i)
        {
            src.push_back(x);
            //std::cout << x << ' ';
        }
    }

    return src;
}

src_vec_t generate()
{
    //return generate_e();
    return generate_ep();
}

int trivial(const src_vec_t& src, interval_t qi)
{
    int count = 0;
    int majorityElement = 0; // will be assigned before use for valid args

    for (int i = qi.first; i <= qi.second; ++i)
    {
        if (count == 0)
            majorityElement = src[i];

        if (src[i] == majorityElement) 
           ++count;
        else 
           --count;
    }

    count = 0;
    for (int i = qi.first; i <= qi.second; ++i)
    {
        if (src[i] == majorityElement)
            count++;
    }

    if (2 * count > qi.second + 1 - qi.first)
        return majorityElement;
    else
        return None;
}

index_map_t sort_ind(const src_vec_t& src)
{
    int ind = 0;
    index_map_t im;

    for (auto x: src)
        im[x].push_back(ind++);

    return im;
}

weight_vec_t get_weights(const index_vec_t& indexes)
{
    weight_vec_t weights;

    for (int i = 0; i != int(indexes.size()); ++i)
        weights.push_back(2 * i - indexes[i]);

    return weights;
}

pair_vec_t get_prefix(const index_vec_t& indexes, const weight_vec_t& weights)
{
    pair_vec_t prefix;

    for (int i = 0; i != int(indexes.size()); ++i)
        if (prefix.empty() || weights[i] < prefix.back().second)
            prefix.emplace_back(indexes[i], weights[i]);

    return prefix;
}

pair_vec_t get_suffix(const index_vec_t& indexes, const weight_vec_t& weights)
{
    pair_vec_t suffix;

    for (int i = indexes.size() - 1; i >= 0; --i)
        if (suffix.empty() || weights[i] > suffix.back().second)
            suffix.emplace_back(indexes[i], weights[i]);

    std::reverse(suffix.begin(), suffix.end());
    return suffix;
}

interval_vec_t get_intervals(const pair_vec_t& prefix, const pair_vec_t& suffix)
{
    interval_vec_t intervals;
    int prev_suffix_index = 0; // will be assigned before use for correct args
    int prev_suffix_weight = 0; // same assumptions

    for (int ind_pref = 0, ind_suff = 0; ind_pref != int(prefix.size());)
    {
        auto i_pref = prefix[ind_pref].first;
        auto w_pref = prefix[ind_pref].second;

        if (ind_suff != int(suffix.size()))
        {
            auto i_suff = suffix[ind_suff].first;
            auto w_suff = suffix[ind_suff].second;

            if (w_pref <= w_suff)
            {
                auto beg = std::max(0, i_pref + w_pref - w_suff);

                if (i_pref < i_suff)
                    intervals.emplace_back(beg, i_suff + 1);

                if (w_pref == w_suff)
                    ++ind_pref;

                ++ind_suff;
                prev_suffix_index = i_suff;
                prev_suffix_weight = w_suff;
                continue;
            }
        }

        // ind_suff out of bounds or w_pref > w_suff:
        auto end = prev_suffix_index + prev_suffix_weight - w_pref + 1;
        // end may be out-of-bounds; that's OK if overflow is not possible
        intervals.emplace_back(i_pref, end);
        ++ind_pref;
    }

    return intervals;
}

interval_vec_t merge(const interval_vec_t& from)
{
    using endpoints_t = std::vector<std::pair<int, bool>>;
    endpoints_t ep(2 * from.size());

    std::transform(from.begin(), from.end(), ep.begin(),
                   [](interval_t x){ return std::make_pair(x.first, true); });

    std::transform(from.begin(), from.end(), ep.begin() + from.size(),
                   [](interval_t x){ return std::make_pair(x.second, false); });

    std::sort(ep.begin(), ep.end());

    interval_vec_t to;
    int start; // will be assigned before use for correct args
    int overlaps = 0;

    for (auto& x: ep)
    {
        if (x.second) // begin
        {
            if (overlaps++ == 0)
                start = x.first;
        }
        else // end
        {
            if (--overlaps == 0)
                to.emplace_back(start, x.first);
        }
    }

    return to;
}

interval_vec_t get_intervals(const index_vec_t& indexes)
{
    auto weights = get_weights(indexes);
    auto prefix = get_prefix(indexes, weights);
    auto suffix = get_suffix(indexes, weights);
    auto intervals = get_intervals(prefix, suffix);
    return merge(intervals);
}

void update_qv(
    query_vec_t& qv,
    int value,
    const interval_vec_t& intervals,
    const index_vec_t& iv)
{
    int iv_ind = 0;
    int qv_ind = 0;
    int accum = 0;

    for (auto& interval: intervals)
    {
        int i_begin = interval.first;
        int i_end = std::min<int>(interval.second, qv.size() - 1);

        while (iv[iv_ind] < i_begin)
        {
            ++accum;
            ++iv_ind;
        }

        qv_ind = std::max(qv_ind, i_begin);

        while (qv_ind <= i_end)
        {
            qv[qv_ind].emplace_back(value, accum);

            if (iv[iv_ind] == qv_ind)
            {
                ++accum;
                ++iv_ind;
            }

            ++qv_ind;
        }
    }
}

void print_preprocess_stat(const index_map_t& im, const query_vec_t& qv)
{
    double sum_coverage = 0.;
    int max_coverage = 0;

    for (auto& x: qv)
    {
        sum_coverage += x.size();
        max_coverage = std::max<int>(max_coverage, x.size());
    }

    std::cout << "             size = " << qv.size() - 1 << '\n';
    std::cout << "           values = " << im.size() << '\n';
    std::cout << "     max coverage = " << max_coverage << '\n';
    std::cout << "     avg coverage = " << sum_coverage / qv.size() << '\n';
}

query_vec_t preprocess(const src_vec_t& src)
{
    query_vec_t qv(src.size() + 1);
    auto im = sort_ind(src);

    for (auto& val: im)
    {
        auto intervals = get_intervals(val.second);
        update_qv(qv, val.first, intervals, val.second);
    }

    print_preprocess_stat(im, qv);
    return qv;
}

int do_query(const src_vec_t& src, const query_vec_t& qv, interval_t qi)
{
    if (qi.first == qi.second)
        return src[qi.first];

    auto b = qv[qi.first].begin();
    auto e = qv[qi.second + 1].begin();

    while (b != qv[qi.first].end() && e != qv[qi.second + 1].end())
    {
        if (b->first < e->first)
        {
            ++b;
        }
        else if (e->first < b->first)
        {
            ++e;
        }
        else // if (e->first == b->first)
        {
            // hope this doesn't overflow
            if (2 * (e->second - b->second) > qi.second + 1 - qi.first)
                return b->first;

            ++b;
            ++e;
        }
    }

    return None;
}

int main()
{
    std::random_device rd;
    std::default_random_engine eng{rd()};
    auto poisson = std::bind(std::poisson_distribution<int>{500}, eng);
    int majority = 0;
    int nonzero = 0;
    int failed = 0;

    auto src = generate();
    auto qv = preprocess(src);

    for (int i = 0; i < NQueries; ++i)
    {
        int size = poisson();
        auto ud = std::uniform_int_distribution<int>(0, src.size() - size - 1);
        int start = ud(eng);
        int stop = start + size;
        auto res1 = do_query(src, qv, {start, stop});
        auto res2 = trivial(src, {start, stop});
        //std::cout << size << ": " << res1 << ' ' << res2 << '\n';

        if (res2 != res1)
            ++failed;

        if (res2 != None)
        {
            ++majority;

            if (res2 != 0)
                ++nonzero;
        }
    }

    std::cout << "majority elements = " << 100. * majority / NQueries << "%\n";
    std::cout << " nonzero elements = " << 100. * nonzero / NQueries << "%\n";
    std::cout << "          queries = " << NQueries << '\n';
    std::cout << "           failed = " << failed << '\n';

    return 0;
}

travaux annexes:

comme indiqué dans autre réponse à cette question , il y a d'autres travaux où ce problème est déjà résolu: " gamme Majorité dans le temps constant et l'espace linéaire "par S. Durocher, M. He, I Munro, P. K. Nicholson, M. Skala .

algorithme présenté dans cet article a de meilleures complexités asymptotiques pour heure d'interrogation: O(1) au lieu de O(log n) et pour l'espace: O(n) au lieu de O(n log n) .

une meilleure complexité de l'espace permet à cet algorithme de traiter des ensembles de données plus grands (en les comparant à l'algorithme proposé dans cette réponse). Moins de mémoire nécessaire pour les données pré-traitées et un modèle d'accès aux données plus régulier, très probablement, permettent à cet algorithme de pré-traiter les données plus rapidement. Mais il n'est pas facile avec la requête...

supposons nous avons les données d'entrée les plus favorables à l'algorithme du papier: n=1000000000 (il est difficile d'imaginer un système avec plus de 10..30 gigaoctets de mémoire, en 2013).

algorithme proposé dans cette réponse doit traiter jusqu'à 120 (ou 2 limites de requête * 2 * log n) éléments pour chaque requête. Mais il effectue des opérations très simples, similaires à la recherche linéaire. Et il accède séquentiellement à deux zones de mémoire contiguës, donc il est facile à mettre en cache.

L'algorithme du papier doit effectuer jusqu'à 20 opérations (ou 2 limites de requête * 5 candidats * 2 niveaux d'arbre en ondelettes) pour chaque requête. C'est 6 fois moins. Mais chaque opération est plus complexe. Chaque requête pour représentation succincte des compteurs de bits contient elle-même une recherche linéaire (ce qui signifie 20 recherches linéaires au lieu d'une). Pire que tout, chaque opération de ce type devrait accéder à plusieurs zones de mémoire indépendantes( à moins que la taille de la requête et donc la taille quadruple est très petite), donc la requête est cache-hostiles. Ce qui signifie que chaque requête (alors est une opération à temps constant) est assez lente, probablement plus lente que dans l'algorithme proposé ici. Si nous diminuons la taille du tableau d'entrées, augmentées sont les chances que l'algorithme proposé ici est plus rapide.

inconvénient pratique de l'algorithme dans le papier est l'arbre des ondelettes et succinct bit counter implémentation. Leur mise en œuvre à partir de zéro peut prendre beaucoup de temps. Utiliser une implémentation préexistante n'est pas toujours pratique.