Liste de Big - O pour les fonctions PHP

Puisqu'il ne semble pas que quelqu'un a fait cela avant que je pensais que ce serait une bonne idée de l'avoir pour référence quelque part. J'y suis allé soit par benchmark soit par code-skimming pour caractériser les fonctions array_* . J'ai essayé de mettre le plus intéressant Big-O en haut. Cette liste n'est pas complète.

Note: Tout le Big-O où calculé en supposant une recherche de hachage est O(1) même si c'est vraiment O(n). Le coefficient de n est si faible, le le fait de stocker un tableau suffisamment grand vous nuirait avant que les caractéristiques de lookup Big-O commencent à prendre effet. Par exemple, la différence entre un appel à array_key_exists à N=1 et N=1.000.000 est une augmentation de temps d'environ 50%.

Points Intéressants :

1. isset / array_key_exists est beaucoup plus rapide que in_array et array_search
2. + (union) est un peu plus rapide que array_merge (et semble plus agréable). Mais il fonctionne différemment donc, gardez cela à l'esprit.
3. shuffle est sur le même Big-O tier array_rand
4. array_pop / array_push est plus rapide que array_shift / array_unshift en raison de la pénalité de réindexation

"Lookup :

array_key_exists O (n) mais vraiment proche de O (1) - Ceci est dû au sondage linéaire en les collisions, mais parce que les chances de collision est très faible, le coefficient est également très faible. Par exemple, la différence entre N=1000 et N=100000 ne ralentit que de 50% environ.

isset( $array[$index] ) O(n) mais vraiment proche de O(1) - il utilise la même recherche que array_key_exists. Depuis sa construction de langage, va mettre en cache la recherche Si la clé est codée en dur, résultant en une accélération dans les cas où la même la clé est utilisée de façon répétée.

in_array O(n) - c'est parce qu'il fait une recherche linéaire à travers le tableau jusqu'à ce qu'il trouve la valeur.

array_search O(n) - il utilise la même fonction de base que in_array mais renvoie de la valeur.

fonctions de file d'attente :

array_push O (∑var_i, pour tous i)

array_pop O (1)

array_shift O(n) - c'est à réindexer toutes les clés

array_unshift O(n + ∑ var_i, pour tout i), il a pour réindexer toutes les clés

Matrice D'Intersection, Union, Soustraction :

array_intersect_key si l'intersection de 100% ne O(Max(param_i_size)*∑param_i_count, pour tout i), si l'intersection de 0% se coupent en O(∑param_i_size, pour tout i)

array_intersect si l'intersection de 100% ne O(n^2*∑param_i_count, pour tout i), si l'intersection de 0% se coupent en O(n^2)

array_intersect_assoc si l'intersection de 100% ne O(Max(param_i_size)*∑param_i_count, pour tout i), si l'intersection de 0% se coupent en O(∑param_i_size, pour tout i)

array_diff O(π param_i_size, pour tous les i)) Que du produit de tous les param_sizes

array_diff_key O(∑ param_i_size, pour moi != 1) - c'est parce que nous n'avons pas besoin d'itérer sur le premier tableau.

array_merge O (∑ array_i, i != 1) - n'a pas besoin d'itérer sur le premier tableau

+ (union) O (n), où n est la taille du 2e tableau (i.e. array_first + array_second) - moins de frais généraux que array_merge puisqu'il n'a pas à renuméroter

array_replace O( ∑ array_i, pour tout i )

Aléatoire :

shuffle O(n)

array_rand O(n) - nécessite un sondage linéaire.

Obvious Big-O :

array_fill O (n)

array_fill_keys O (n)

range O (n)

array_splice O (offset + longueur)

array_slice O(offset + longueur) ou O(n) si longueur = NULL

array_keys O (n)

array_values O (n)

array_reverse O (n)

array_pad O (pad_size)

array_flip O (n)

array_sum O (n)

array_product O (n)

array_reduce O (n)

array_filter O (n)

array_map O (n)

array_chunk O (n)

array_combine O (n)

je tiens à remercier Eureqa pour rendre facile de trouver le Big-O des fonctions. C'est un programme incroyable gratuit qui peut trouver la meilleure fonction d'Ajustement pour les données arbitraires.

EDIT:

pour ceux qui doutent que les ID favori de tableau de PHP sont O(N) , j'ai écrit un benchmark pour tester que (ils sont encore effectivement O(1) pour les valeurs les plus réalistes).

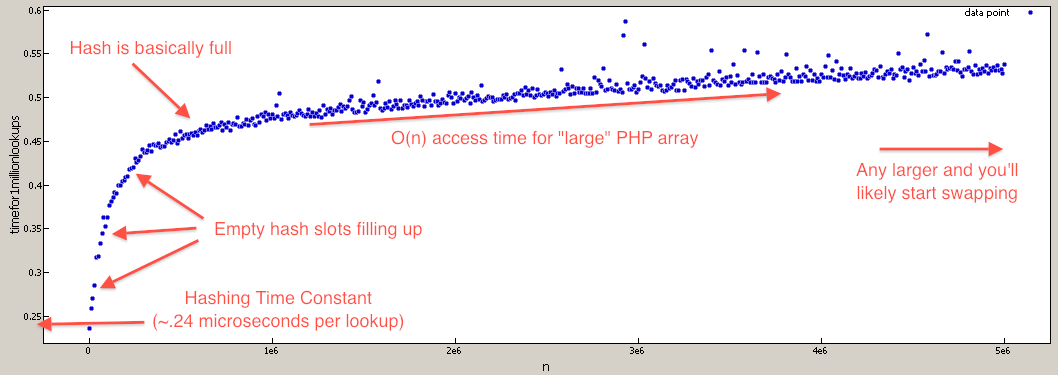
$tests = 1000000;
$max = 5000001;


for( $i = 1; $i <= $max; $i += 10000 ) {
    //create lookup array
    $array = array_fill( 0, $i, NULL );

    //build test indexes
    $test_indexes = array();
    for( $j = 0; $j < $tests; $j++ ) {
        $test_indexes[] = rand( 0, $i-1 );
    }

    //benchmark array lookups
    $start = microtime( TRUE );
    foreach( $test_indexes as $test_index ) {
        $value = $array[ $test_index ];
        unset( $value );
    }
    $stop = microtime( TRUE );
    unset( $array, $test_indexes, $test_index );

    printf( "%d,%1.15f\n", $i, $stop - $start ); //time per 1mil lookups
    unset( $stop, $start );
}