Distance Levenshtein: comment mieux gérer les échanges de mots?
j'ai eu un certain succès en comparant les chaînes en utilisant la fonction PHP levenshtein .
Cependant, pour deux chaînes qui contiennent des substrats qui ont changé de position, l'algorithme compte ceux-ci comme de nouveaux substrats entiers.
par exemple:
levenshtein("The quick brown fox", "brown quick The fox"); // 10 differences
sont considérés comme ayant moins en commun que:
levenshtein("The quick brown fox", "The quiet swine flu"); // 9 differences
je préférerais un algorithme qui ont vu que le deux premiers étaient plus similaires.
Comment pourrais-je trouver une fonction de comparaison capable d'identifier les substrats qui ont changé de position comme étant distincts des modifications?
une approche possible à laquelle j'ai pensé est de mettre tous les mots de la chaîne dans l'ordre alphabétique, avant la comparaison. Cela enlève complètement l'ordre original des mots de la comparaison. Un inconvénient à cela, cependant, est-ce que changer juste la première lettre d'un mot peut créer une perturbation beaucoup plus grande qu'un changement d'une seule lettre devrait causer.
ce que j'essaie d'obtenir est de comparer deux faits sur les gens qui sont des chaînes de texte libres, et de décider comment ces faits sont susceptibles d'indiquer le même fait. Les faits peuvent être l'école fréquentée, le nom de l'employeur ou de l'éditeur, par exemple. Deux documents peuvent avoir la même école orthographiée différemment, mots dans un ordre différent, mots supplémentaires, etc, de sorte que l'appariement doit être un peu flou si nous devons faire une bonne supposition qu'ils se réfèrent à la même école. Jusqu'à présent, il fonctionne très bien pour les fautes d'orthographe (j'utilise un algorithme phénétique similaire à métaphone en plus de tout cela) mais très mal si vous changez l'ordre des mots autour de qui semblent communs dans une école: "xxx collège" vs "collège de xxx".
9 réponses
n-grammes
utiliser n-grammes , qui supporte transpositions à plusieurs caractères dans le texte entier .
l'idée générale est que vous divisez les deux chaînes en deux ou trois sous-chaînes (n-grammes) et traitez le nombre de n-grammes partagés entre les deux chaînes comme leur métrique de similarité. Cela peut ensuite être normalisé en divisant le nombre partagé par le total nombre de n-grammes dans la longue chaîne. C'est facile à calculer, mais assez puissant.
pour les phrases types:
A. The quick brown fox
B. brown quick The fox
C. The quiet swine flu
A et b part 18 2-grammes
A et c part seulement 8 2-grammes
sur 20 total possible.
cela a été discutés plus en détail dans le Gravano et coll. papier .
tf-idf et de la similarité cosinus
une alternative pas si insignifiante, mais fondée sur la théorie de l'information, serait d'utiliser le terme fréquence des termes–fréquence inverse des documents (TF-idf) pour peser les jetons, construire des vecteurs de phrases et ensuite utiliser similarité cosinus comme métrique de similarité.
le l'algorithme est:
- calculer les fréquences des jetons de 2 caractères (tf) par phrase.
- calculer les fréquences de phrases inversées (idf), qui est un logarithme d'un quotient du nombre de toutes les phrases dans le corpus (dans ce cas 3) divisé par le nombre de fois qu'un jeton particulier apparaît à travers toutes les phrases. Dans ce cas th est dans toutes les phrases donc il a un contenu d'information zéro (log(3/3)=0).
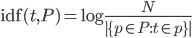
- produire la matrice TF-idf en multipliant les cellules correspondantes dans les tableaux tf et idf.
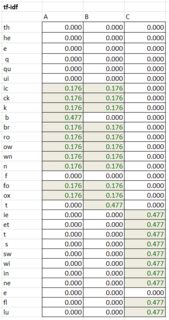
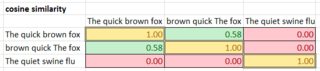
- enfin, calculer la matrice de similarité cosinus pour toutes les paires de phrases, où A et B sont des poids de la table TF-idf pour les jetons correspondants. La fourchette va de 0 (pas similaire) à 1 (égal).
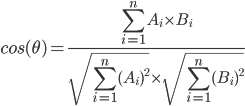
modifications de Levenshtein et Métaphone
concernant les autres réponses. Damerau-Levenshtein la modification appuie seulement la transposition de deux caractères adjacents . Métaphone a été conçu pour correspondre à des mots qui sonnent le même et pas pour la similarité correspondant.
C'est facile. Il suffit d'utiliser la distance Damerau-Levenshtein sur les mots au lieu de lettres.
explose sur les espaces, trie le tableau, implose, puis fait le Levenshtein.
vous pouvez également essayer ceci. (juste une suggestion supplémentaire)
$one = metaphone("The quick brown fox"); // 0KKBRNFKS
$two = metaphone("brown quick The fox"); // BRNKK0FKS
$three = metaphone("The quiet swine flu"); // 0KTSWNFL
similar_text($one, $two, $percent1); // 66.666666666667
similar_text($one, $three, $percent2); // 47.058823529412
similar_text($two, $three, $percent3); // 23.529411764706
cela montrera que le 1er et le 2e sont plus semblables que un et trois et deux et trois.
j'ai implémenté levenshtein dans un correcteur orthographique.
ce que vous demandez, c'est de compter les transpositions comme une édition.
C'est facile, si vous souhaitez seulement de compter les transpositions d'un mot. Toutefois, pour la transposition des mots 2 ou plus loin, l'ajout à l'algorithme est le pire scénario !(max(wordorder1.length(), wordorder2.length())) . Ajouter un sous-algorithme non linéaire à un algorithme déjà quadratique n'est pas une bonne idée.
c'est comment cela pourrait fonctionner.
if (wordorder1[n] == wordorder2[n-1])
{
min(workarray[x-1, y] + 1, workarray[x, y-1] + 1, workarray[x-2, y-2]);
}
else
{
min(workarray[x-1, y] + 1, workarray[x, y-1] + 1);
}
juste pour toucher les transpositions. Si vous voulez toutes les transpositions, vous devez pour chaque position travailler à l'envers à partir de ce point de comparaison
1[n] == 2[n-2].... 1[n] == 2[0]....
alors vous voyez pourquoi ils ne l'incluent pas dans la méthode standard.
Prendre cette réponse et procéder à la modification suivante:
void match(trie t, char* w, string s, int budget){
if (budget < 0) return;
if (*w=='"151900920"') print s;
foreach (char c, subtrie t1 in t){
/* try matching or replacing c */
match(t1, w+1, s+c, (*w==c ? budget : budget-1));
/* try deleting c */
match(t1, w, s, budget-1);
}
/* try inserting *w */
match(t, w+1, s + *w, budget-1);
/* TRY SWAPPING FIRST TWO CHARACTERS */
if (w[1]){
swap(w[0], w[1]);
match(t, w, s, budget-1);
swap(w[0], w[1]);
}
}
Ceci est pour la recherche de dictionnaire dans un tri, mais pour l'appariement à un seul mot, c'est la même idée. Vous faites des branches et des branches, et à n'importe quel moment, vous pouvez faire n'importe quel changement que vous voulez, aussi longtemps que vous lui donnez un coût.
élimine les mots en double entre les deux chaînes et utilise ensuite Levenshtein.
je crois qu'il s'agit d'un bon exemple pour l'utilisation d'un vecteur-moteur de recherche spatiale .
dans cette technique, chaque document devient essentiellement un vecteur ayant autant de dimensions qu'il y a de mots différents dans l'ensemble du corpus; des documents similaires occupent alors des zones voisines dans cet espace vecteur. une belle propriété de ce modèle est que les requêtes sont aussi juste des documents: pour répondre à une requête, vous calculez simplement leur position dans l'espace vectoriel, et vos résultats sont les documents les plus proches que vous pouvez trouver. je suis sûr qu'il y a des solutions "get-and-go" pour PHP là-bas.
pour fuzzifier les résultats à partir de l'espace vectoriel, vous pourriez envisager de faire émulation / similaire technique de traitement du langage naturel, et d'utiliser levenshtein pour construire des requêtes secondaires pour des mots similaires qui se produisent dans votre vocabulaire global.
si la première chaîne est A et la seconde est B:
- fendu A et B en mots
- pour chaque mot dans A, trouver le meilleur mot correspondant dans B (en utilisant levenshtein)
- Supprimer ce mot de B et le mettre dans B* au même index que le mot correspondant dans A.
- Comparez maintenant A et B*
exemple:
A: The quick brown fox
B: Quick blue fox the
B*: the Quick blue fox
vous pourriez améliorer étape 2 en le faisant en plusieurs passes, en ne trouvant que des Correspondances exactes au début, puis en trouvant des correspondances étroites pour les mots en A qui n'ont pas encore de compagnon en B*, puis moins de correspondances étroites, etc.