Java: nombre entier aléatoire avec une distribution non uniforme
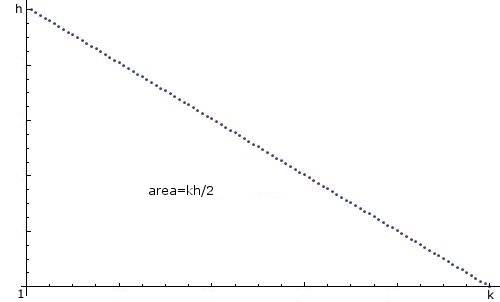
Comment puis-je créer un entier aléatoire n en Java, entre 1 et k avec une "distribution linéaire Décroissante", i.e. 1 est le plus probable, 2 est moins probable, 3 moins probable ...,k moins probable, et les probabilités de descendre de façon linéaire, comme ceci:
je sais qu'il y a déjà des dosens de fils sur ce sujet, et je m'excuse d'en avoir fait un nouveau, mais je ne peux pas sembler être capable de créer ce dont j'ai besoin d'eux. Je sais que l'utilisation de import java.util.*; le code
Random r=new Random();
int n=r.nextInt(k)+1;
crée un entier aléatoire compris entre 1 et k, répartis de manière uniforme.
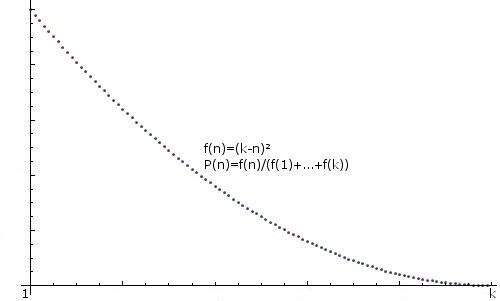
GENERALIZATION: toutes les astuces pour créer un entier distribué arbitrairement, i.e. f(n)=some function,P(n)=f(n)/(f(1)+...+f(k))), serait également appréciée, par exemple:
 .
.
10 réponses
Cela devrait vous donner ce dont vous avez besoin:
public static int getLinnearRandomNumber(int maxSize){
//Get a linearly multiplied random number
int randomMultiplier = maxSize * (maxSize + 1) / 2;
Random r=new Random();
int randomInt = r.nextInt(randomMultiplier);
//Linearly iterate through the possible values to find the correct one
int linearRandomNumber = 0;
for(int i=maxSize; randomInt >= 0; i--){
randomInt -= i;
linearRandomNumber++;
}
return linearRandomNumber;
}
aussi, Voici une solution générale pour les fonctions positives (les fonctions négatives n'ont pas vraiment de sens) le long de la gamme de l'index de début à l'index de stop:
public static int getYourPositiveFunctionRandomNumber(int startIndex, int stopIndex) {
//Generate a random number whose value ranges from 0.0 to the sum of the values of yourFunction for all the possible integer return values from startIndex to stopIndex.
double randomMultiplier = 0;
for (int i = startIndex; i <= stopIndex; i++) {
randomMultiplier += yourFunction(i);//yourFunction(startIndex) + yourFunction(startIndex + 1) + .. yourFunction(stopIndex -1) + yourFunction(stopIndex)
}
Random r = new Random();
double randomDouble = r.nextDouble() * randomMultiplier;
//For each possible integer return value, subtract yourFunction value for that possible return value till you get below 0. Once you get below 0, return the current value.
int yourFunctionRandomNumber = startIndex;
randomDouble = randomDouble - yourFunction(yourFunctionRandomNumber);
while (randomDouble >= 0) {
yourFunctionRandomNumber++;
randomDouble = randomDouble - yourFunction(yourFunctionRandomNumber);
}
return yourFunctionRandomNumber;
}
Note: pour les fonctions qui peuvent retourner des valeurs négatives, une méthode pourrait être de prendre la valeur absolue de cette fonction et de l'appliquer à la solution ci-dessus pour chaque appel de votre fonction.
nous avons donc besoin de la distribution suivante, de la moins probable à la plus probable:
*
**
***
****
*****
etc.
essayons de mapper une variable aléatoire entière uniformément distribuée à cette distribution:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
etc.
de cette façon, si nous générons un entier aléatoire uniformément distribué de 1 à, disons, 15 dans ce cas pour K = 5, nous avons juste besoin de comprendre quel seau il convient. La partie délicate est de savoir comment faire.
Note que les nombres sur la droite sont les nombres triangulaires! Cela signifie que pour généré de façon aléatoire X1T_n, nous avons juste besoin de trouver N tels que T_(n-1) < X <= T_n. Heureusement il y a un formule bien définie pour trouver la "racine triangulaire" d'un nombre donné, que nous pouvons utiliser comme noyau de notre cartographie de la distribution uniforme au seau:
// Assume k is given, via parameter or otherwise
int k;
// Assume also that r has already been initialized as a valid Random instance
Random r = new Random();
// First, generate a number from 1 to T_k
int triangularK = k * (k + 1) / 2;
int x = r.nextInt(triangularK) + 1;
// Next, figure out which bucket x fits into, bounded by
// triangular numbers by taking the triangular root
// We're dealing strictly with positive integers, so we can
// safely ignore the - part of the +/- in the triangular root equation
double triangularRoot = (Math.sqrt(8 * x + 1) - 1) / 2;
int bucket = (int) Math.ceil(triangularRoot);
// Buckets start at 1 as the least likely; we want k to be the least likely
int n = k - bucket + 1;
n devrait maintenant avoir la distribution spécifiée.
il y a beaucoup de façons de faire cela, mais probablement le plus facile est juste de générer
deux entiers aléatoires, entre 0 et k, appelle x, entre 0 et h, appelle y. Si y > mx + b (m et b choisis de façon appropriée...) alors
k-x, else x.
Modifier: répondre aux commentaires ici pour que je puisse avoir un peu plus d'espace.
en gros, ma solution exploite la symétrie votre distribution originale, où p(x) est une fonction linéaire de x. J'ai répondu avant votre édition sur la généralisation, et cette solution ne fonctionne pas dans le cas général (parce qu'il n'y a pas une telle symétrie dans le cas général).
j'ai imaginé le problème comme ceci:
- Vous avez deux triangles de droite, chacun
k x h, avec une hypoténuse commune. La forme composite est unk x hrectangle. - Générer un point aléatoire cela tombe sur chaque point dans le rectangle avec une probabilité égale.
- la Moitié du temps il va tomber dans un triangle, la moitié du temps dans l'autre.
- supposons que la pointe tombe dans le triangle inférieur.
- le triangle décrit essentiellement la F. P. M., et la "hauteur" du triangle au-dessus de chaque valeur de x décrit la probabilité que le point aura une telle valeur de X. (Rappelez-vous que nous ne traitons que des points dans le triangle inférieur.) Donc par le rendement de la x-valeur.
- supposons que la pointe tombe dans le triangle supérieur.
- Inverser les coordonnées et traiter comme ci-dessus avec le triangle inférieur.
vous aurez à prendre soin des cas de bord aussi (je ne me suis pas embêté). Par exemple: Je vois maintenant que votre distribution commence à 1, pas à 0, donc il y a un off-by-one là-dedans, mais c'est facile à réparer.
laissez-moi essayer une autre réponse aussi, inspiré par rlibby. Cette distribution particulière est aussi la distribution de plus petit de deux valeurs choisies uniformément et au hasard dans la même fourchette.
il n'est pas nécessaire de simuler ceci avec des tableaux et autres, si votre distribution est telle que vous pouvez calculer sa fonction de distribution cumulative (cdf). Ci-dessus, vous avez une fonction de distribution de probabilité (pdf). h est en fait déterminé, puisque l'aire sous la courbe doit être 1. Pour simplifier les mathématiques,laissez-moi aussi supposer que vous choisissez un nombre dans [0, k).
Le fichier pdf ici est f(x) = (2/k) * (1 - x/k), si je vous lis à droite. Le cdf n'est qu'une partie intégrante du pdf. Ici, C'est F(x) = (2 / k) * (x - x^2 / 2k). (Vous pouvez répéter cette logique pour toute fonction pdf si elle est intégrable.)
alors vous devez calculer l'inverse de la fonction cdf, F^-1(x) et si je n'étais pas paresseux, je le ferais pour vous.
mais la bonne nouvelle est ceci: une fois que vous avez F^-1(x), Tout ce que vous faites est de l'appliquer à une distribution de valeur aléatoire uniformément dans [0,1] et d'appliquer la fonction à elle. Java.util.Le hasard peut fournir cela avec un certain soin. C'est votre valeur échantillonnée au hasard à partir de votre distribution.
c'est ce qu'on appelle une distribution triangulaire, bien que le vôtre soit un cas dégénéré avec le mode égal à la valeur minimale. Wikipedia a des équations pour créer une variable donnée uniformément distribuée (0,1).
La première solution qui vient à l'esprit est d'utiliser le blocage d'un tableau. Chaque indice spécifierait une fourchette de valeurs en fonction de la façon dont "probable" vous voulez qu'il soit. Dans ce cas, vous utiliserez une gamme plus large pour 1, moins large pour 2, et ainsi de suite jusqu'à ce que vous atteigniez une petite valeur (disons 1) pour K.
int [] indexBound = new int[k];
int prevBound =0;
for(int i=0;i<k;i++){
indexBound[i] = prevBound+prob(i);
prevBound=indexBound[i];
}
int r = new Random().nextInt(prevBound);
for(int i=0;i<k;i++){
if(r > indexBound[i];
return i;
}
maintenant le problème est juste de trouver un nombre aléatoire, et puis mapping ce nombre à son seau. vous pouvez le faire pour n'importe quelle distribution pour autant que vous puissiez discrétiser la largeur de chaque intervalle. Faites-moi savoir si je manque quelque chose en expliquant l'algorithme ou sa justesse. Inutile de dire que ce qui doit être optimisé.
quelque Chose comme ça....
class DiscreteDistribution
{
// cumulative distribution
final private double[] cdf;
final private int k;
public DiscreteDistribution(Function<Integer, Double> pdf, int k)
{
this.k = k;
this.cdf = new double[k];
double S = 0;
for (int i = 0; i < k; ++i)
{
double p = pdf.apply(i+1);
S += p;
this.cdf[i] = S;
}
for (int i = 0; i < k; ++i)
{
this.cdf[i] /= S;
}
}
/**
* transform a cumulative distribution between 0 (inclusive) and 1 (exclusive)
* to an integer between 1 and k.
*/
public int transform(double q)
{
// exercise for the reader:
// binary search on cdf for the lowest index i where q < cdf[i]
// return this number + 1 (to get into a 1-based index.
// If q >= 1, return k.
}
}
la fonction de Distribution Cumulative est x^2 pour une distribution triangulaire [0,1] avec le mode (plus forte probabilité pondérée) de 1, comme indiqué ici.
Donc, tout ce que nous devons faire pour transformer une distribution uniforme (comme Java Random::nextDouble) dans une distribution triangulaire pratique pondérée vers 1 est: il suffit de prendre la racine carrée Math.sqrt(rand.nextDouble()), qui peut alors être multiplié par n'importe quelle plage désirée.
Pour ton exemple:
int a = 1; // lower bound, inclusive
int b = k; // upper bound, exclusive
double weightedRand = Math.sqrt(rand.nextDouble()); // use triangular distribution
weightedRand = 1.0 - weightedRand; // invert the distribution (greater density at bottom)
int result = (int) Math.floor((b-a) * weightedRand);
result += a; // offset by lower bound
if(result >= b) result = a; // handle the edge case
La chose la plus simple à faire pour générer une liste ou un tableau de toutes les valeurs possibles de leur poids.
int k = /* possible values */
int[] results = new int[k*(k+1)/2];
for(int i=1,r=0;i<=k;i++)
for(int j=0;j<=k-i;j++)
results[r++] = i;
// k=4 => { 1,1,1,1,2,2,2,3,3,4 }
// to get a value with a given distribution.
int n = results[random.nextInt(results.length)];
ceci fonctionne le mieux pour des valeurs de k relativement petites.ie. k < 1000. ;)
pour les plus grands nombres vous pouvez utiliser une approche de seau
int k =
int[] buckets = new int[k+1];
for(int i=1;i<k;i++)
buckets[i] = buckets[i-1] + k - i + 1;
int r = random.nextInt(buckets[buckets.length-1]);
int n = Arrays.binarySearch(buckets, r);
n = n < 0 ? -n : n + 1;
Le coût de la recherche binaire est assez petite, mais pas aussi efficace qu'une consultation directe (pour un petit tableau)
pour une distribution arbitaire vous pouvez utiliser un double[] pour les distribution cumulative et utilisez une recherche binaire pour trouver la valeur.