Est-il un moyen de détecter si une image est floue?

Une autre façon très simple d'estimer la netteté d'une image est d'utiliser un filtre Laplace (ou LoG) et de choisir simplement la valeur maximale. Utiliser une mesure robuste comme un quantile à 99,9% est probablement mieux si vous attendez du bruit (c'est-à-dire choisir le nième contraste le plus élevé au lieu du contraste le plus élevé.) Si vous prévoyez une luminosité variable de l'image, vous devez également inclure une étape de prétraitement pour normaliser la luminosité/contraste de l'image (par exemple, l'égalisation de l'histogramme).

J'ai implémenté la suggestion de Simon et celui-ci dans Mathematica, et l'a essayé sur quelques images de test:

Le premier test brouille les images de test en utilisant un filtre gaussien avec une taille de noyau variable, puis calcule la FFT de l'image floue et prend la moyenne des fréquences les plus élevées de 90%:

testFft[img_] := Table[
  (
   blurred = GaussianFilter[img, r];
   fft = Fourier[ImageData[blurred]];
   {w, h} = Dimensions[fft];
   windowSize = Round[w/2.1];
   Mean[Flatten[(Abs[
       fft[[w/2 - windowSize ;; w/2 + windowSize, 
         h/2 - windowSize ;; h/2 + windowSize]]])]]
   ), {r, 0, 10, 0.5}]

Résultat d'un tracé logarithmique:

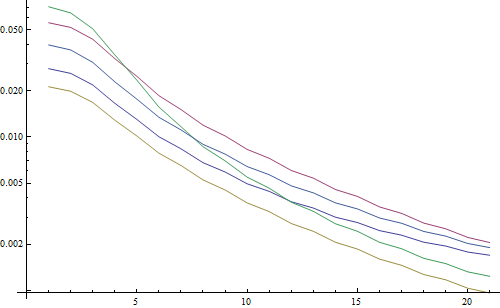
Les 5 lignes représentent les 5 images de test, l'axe X représente le rayon du filtre gaussien. Les graphiques sont en baisse, donc la FFT est un bon mesure de la netteté.

C'est le code de l'estimateur de flou "le plus élevé": il applique simplement un filtre de journal et renvoie le pixel le plus brillant dans le résultat du filtre:

testLaplacian[img_] := Table[
  (
   blurred = GaussianFilter[img, r];
   Max[Flatten[ImageData[LaplacianGaussianFilter[blurred, 1]]]];
   ), {r, 0, 10, 0.5}]

Résultat d'un tracé logarithmique:

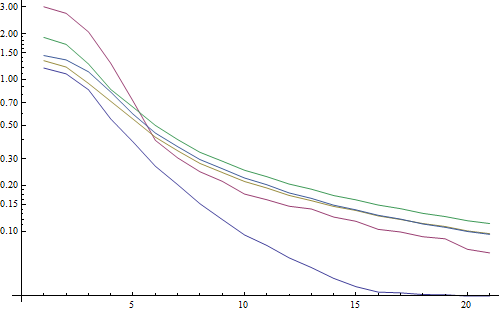
L'écart pour les images non floues est un peu meilleur ici (2.5 vs 3.3), principalement parce que cette méthode n'utilise que le contraste le plus fort dans l'image, alors que la FFT est essentiellement une moyenne sur l'image entière. Les fonctions sont également décroissant plus rapidement, il pourrait donc être plus facile de définir un seuil "flou".

Au cours d'un travail avec un objectif de mise au point automatique, je suis tombé sur cet ensemble très utile d'algorithmes pour détecter la mise au point de l'image. Il est implémenté dans MATLAB, mais la plupart des fonctions sont assez faciles à porter vers OpenCV avec filter2D.

C'est essentiellement une implémentation d'enquête de nombreux algorithmes de mesure de mise au point. Si vous voulez lire les documents originaux, les références aux auteurs des algorithmes sont fournies dans le code. La 2012 de papier par Pertuz, et al. analyse de focus measure operators for shape de focus (SFF) donne un excellent aperçu de toutes ces mesures ainsi que de leurs performances (à la fois en termes de vitesse et de précision appliquées à SFF).

EDIT: ajout du code MATLAB juste au cas où le lien meurt.

function FM = fmeasure(Image, Measure, ROI)
%This function measures the relative degree of focus of 
%an image. It may be invoked as:
%
%   FM = fmeasure(Image, Method, ROI)
%
%Where 
%   Image,  is a grayscale image and FM is the computed
%           focus value.
%   Method, is the focus measure algorithm as a string.
%           see 'operators.txt' for a list of focus 
%           measure methods. 
%   ROI,    Image ROI as a rectangle [xo yo width heigth].
%           if an empty argument is passed, the whole
%           image is processed.
%
%  Said Pertuz
%  Abr/2010


if ~isempty(ROI)
    Image = imcrop(Image, ROI);
end

WSize = 15; % Size of local window (only some operators)

switch upper(Measure)
    case 'ACMO' % Absolute Central Moment (Shirvaikar2004)
        if ~isinteger(Image), Image = im2uint8(Image);
        end
        FM = AcMomentum(Image);

    case 'BREN' % Brenner's (Santos97)
        [M N] = size(Image);
        DH = Image;
        DV = Image;
        DH(1:M-2,:) = diff(Image,2,1);
        DV(:,1:N-2) = diff(Image,2,2);
        FM = max(DH, DV);        
        FM = FM.^2;
        FM = mean2(FM);

    case 'CONT' % Image contrast (Nanda2001)
        ImContrast = inline('sum(abs(x(:)-x(5)))');
        FM = nlfilter(Image, [3 3], ImContrast);
        FM = mean2(FM);

    case 'CURV' % Image Curvature (Helmli2001)
        if ~isinteger(Image), Image = im2uint8(Image);
        end
        M1 = [-1 0 1;-1 0 1;-1 0 1];
        M2 = [1 0 1;1 0 1;1 0 1];
        P0 = imfilter(Image, M1, 'replicate', 'conv')/6;
        P1 = imfilter(Image, M1', 'replicate', 'conv')/6;
        P2 = 3*imfilter(Image, M2, 'replicate', 'conv')/10 ...
            -imfilter(Image, M2', 'replicate', 'conv')/5;
        P3 = -imfilter(Image, M2, 'replicate', 'conv')/5 ...
            +3*imfilter(Image, M2, 'replicate', 'conv')/10;
        FM = abs(P0) + abs(P1) + abs(P2) + abs(P3);
        FM = mean2(FM);

    case 'DCTE' % DCT energy ratio (Shen2006)
        FM = nlfilter(Image, [8 8], @DctRatio);
        FM = mean2(FM);

    case 'DCTR' % DCT reduced energy ratio (Lee2009)
        FM = nlfilter(Image, [8 8], @ReRatio);
        FM = mean2(FM);

    case 'GDER' % Gaussian derivative (Geusebroek2000)        
        N = floor(WSize/2);
        sig = N/2.5;
        [x,y] = meshgrid(-N:N, -N:N);
        G = exp(-(x.^2+y.^2)/(2*sig^2))/(2*pi*sig);
        Gx = -x.*G/(sig^2);Gx = Gx/sum(Gx(:));
        Gy = -y.*G/(sig^2);Gy = Gy/sum(Gy(:));
        Rx = imfilter(double(Image), Gx, 'conv', 'replicate');
        Ry = imfilter(double(Image), Gy, 'conv', 'replicate');
        FM = Rx.^2+Ry.^2;
        FM = mean2(FM);

    case 'GLVA' % Graylevel variance (Krotkov86)
        FM = std2(Image);

    case 'GLLV' %Graylevel local variance (Pech2000)        
        LVar = stdfilt(Image, ones(WSize,WSize)).^2;
        FM = std2(LVar)^2;

    case 'GLVN' % Normalized GLV (Santos97)
        FM = std2(Image)^2/mean2(Image);

    case 'GRAE' % Energy of gradient (Subbarao92a)
        Ix = Image;
        Iy = Image;
        Iy(1:end-1,:) = diff(Image, 1, 1);
        Ix(:,1:end-1) = diff(Image, 1, 2);
        FM = Ix.^2 + Iy.^2;
        FM = mean2(FM);

    case 'GRAT' % Thresholded gradient (Snatos97)
        Th = 0; %Threshold
        Ix = Image;
        Iy = Image;
        Iy(1:end-1,:) = diff(Image, 1, 1);
        Ix(:,1:end-1) = diff(Image, 1, 2);
        FM = max(abs(Ix), abs(Iy));
        FM(FM<Th)=0;
        FM = sum(FM(:))/sum(sum(FM~=0));

    case 'GRAS' % Squared gradient (Eskicioglu95)
        Ix = diff(Image, 1, 2);
        FM = Ix.^2;
        FM = mean2(FM);

    case 'HELM' %Helmli's mean method (Helmli2001)        
        MEANF = fspecial('average',[WSize WSize]);
        U = imfilter(Image, MEANF, 'replicate');
        R1 = U./Image;
        R1(Image==0)=1;
        index = (U>Image);
        FM = 1./R1;
        FM(index) = R1(index);
        FM = mean2(FM);

    case 'HISE' % Histogram entropy (Krotkov86)
        FM = entropy(Image);

    case 'HISR' % Histogram range (Firestone91)
        FM = max(Image(:))-min(Image(:));


    case 'LAPE' % Energy of laplacian (Subbarao92a)
        LAP = fspecial('laplacian');
        FM = imfilter(Image, LAP, 'replicate', 'conv');
        FM = mean2(FM.^2);

    case 'LAPM' % Modified Laplacian (Nayar89)
        M = [-1 2 -1];        
        Lx = imfilter(Image, M, 'replicate', 'conv');
        Ly = imfilter(Image, M', 'replicate', 'conv');
        FM = abs(Lx) + abs(Ly);
        FM = mean2(FM);

    case 'LAPV' % Variance of laplacian (Pech2000)
        LAP = fspecial('laplacian');
        ILAP = imfilter(Image, LAP, 'replicate', 'conv');
        FM = std2(ILAP)^2;

    case 'LAPD' % Diagonal laplacian (Thelen2009)
        M1 = [-1 2 -1];
        M2 = [0 0 -1;0 2 0;-1 0 0]/sqrt(2);
        M3 = [-1 0 0;0 2 0;0 0 -1]/sqrt(2);
        F1 = imfilter(Image, M1, 'replicate', 'conv');
        F2 = imfilter(Image, M2, 'replicate', 'conv');
        F3 = imfilter(Image, M3, 'replicate', 'conv');
        F4 = imfilter(Image, M1', 'replicate', 'conv');
        FM = abs(F1) + abs(F2) + abs(F3) + abs(F4);
        FM = mean2(FM);

    case 'SFIL' %Steerable filters (Minhas2009)
        % Angles = [0 45 90 135 180 225 270 315];
        N = floor(WSize/2);
        sig = N/2.5;
        [x,y] = meshgrid(-N:N, -N:N);
        G = exp(-(x.^2+y.^2)/(2*sig^2))/(2*pi*sig);
        Gx = -x.*G/(sig^2);Gx = Gx/sum(Gx(:));
        Gy = -y.*G/(sig^2);Gy = Gy/sum(Gy(:));
        R(:,:,1) = imfilter(double(Image), Gx, 'conv', 'replicate');
        R(:,:,2) = imfilter(double(Image), Gy, 'conv', 'replicate');
        R(:,:,3) = cosd(45)*R(:,:,1)+sind(45)*R(:,:,2);
        R(:,:,4) = cosd(135)*R(:,:,1)+sind(135)*R(:,:,2);
        R(:,:,5) = cosd(180)*R(:,:,1)+sind(180)*R(:,:,2);
        R(:,:,6) = cosd(225)*R(:,:,1)+sind(225)*R(:,:,2);
        R(:,:,7) = cosd(270)*R(:,:,1)+sind(270)*R(:,:,2);
        R(:,:,7) = cosd(315)*R(:,:,1)+sind(315)*R(:,:,2);
        FM = max(R,[],3);
        FM = mean2(FM);

    case 'SFRQ' % Spatial frequency (Eskicioglu95)
        Ix = Image;
        Iy = Image;
        Ix(:,1:end-1) = diff(Image, 1, 2);
        Iy(1:end-1,:) = diff(Image, 1, 1);
        FM = mean2(sqrt(double(Iy.^2+Ix.^2)));

    case 'TENG'% Tenengrad (Krotkov86)
        Sx = fspecial('sobel');
        Gx = imfilter(double(Image), Sx, 'replicate', 'conv');
        Gy = imfilter(double(Image), Sx', 'replicate', 'conv');
        FM = Gx.^2 + Gy.^2;
        FM = mean2(FM);

    case 'TENV' % Tenengrad variance (Pech2000)
        Sx = fspecial('sobel');
        Gx = imfilter(double(Image), Sx, 'replicate', 'conv');
        Gy = imfilter(double(Image), Sx', 'replicate', 'conv');
        G = Gx.^2 + Gy.^2;
        FM = std2(G)^2;

    case 'VOLA' % Vollath's correlation (Santos97)
        Image = double(Image);
        I1 = Image; I1(1:end-1,:) = Image(2:end,:);
        I2 = Image; I2(1:end-2,:) = Image(3:end,:);
        Image = Image.*(I1-I2);
        FM = mean2(Image);

    case 'WAVS' %Sum of Wavelet coeffs (Yang2003)
        [C,S] = wavedec2(Image, 1, 'db6');
        H = wrcoef2('h', C, S, 'db6', 1);   
        V = wrcoef2('v', C, S, 'db6', 1);   
        D = wrcoef2('d', C, S, 'db6', 1);   
        FM = abs(H) + abs(V) + abs(D);
        FM = mean2(FM);

    case 'WAVV' %Variance of  Wav...(Yang2003)
        [C,S] = wavedec2(Image, 1, 'db6');
        H = abs(wrcoef2('h', C, S, 'db6', 1));
        V = abs(wrcoef2('v', C, S, 'db6', 1));
        D = abs(wrcoef2('d', C, S, 'db6', 1));
        FM = std2(H)^2+std2(V)+std2(D);

    case 'WAVR'
        [C,S] = wavedec2(Image, 3, 'db6');
        H = abs(wrcoef2('h', C, S, 'db6', 1));   
        V = abs(wrcoef2('v', C, S, 'db6', 1));   
        D = abs(wrcoef2('d', C, S, 'db6', 1)); 
        A1 = abs(wrcoef2('a', C, S, 'db6', 1));
        A2 = abs(wrcoef2('a', C, S, 'db6', 2));
        A3 = abs(wrcoef2('a', C, S, 'db6', 3));
        A = A1 + A2 + A3;
        WH = H.^2 + V.^2 + D.^2;
        WH = mean2(WH);
        WL = mean2(A);
        FM = WH/WL;
    otherwise
        error('Unknown measure %s',upper(Measure))
end
 end
%************************************************************************
function fm = AcMomentum(Image)
[M N] = size(Image);
Hist = imhist(Image)/(M*N);
Hist = abs((0:255)-255*mean2(Image))'.*Hist;
fm = sum(Hist);
end

%******************************************************************
function fm = DctRatio(M)
MT = dct2(M).^2;
fm = (sum(MT(:))-MT(1,1))/MT(1,1);
end

%************************************************************************
function fm = ReRatio(M)
M = dct2(M);
fm = (M(1,2)^2+M(1,3)^2+M(2,1)^2+M(2,2)^2+M(3,1)^2)/(M(1,1)^2);
end
%******************************************************************

Quelques exemples de versions D'OpenCV:

// OpenCV port of 'LAPM' algorithm (Nayar89)
double modifiedLaplacian(const cv::Mat& src)
{
    cv::Mat M = (Mat_<double>(3, 1) << -1, 2, -1);
    cv::Mat G = cv::getGaussianKernel(3, -1, CV_64F);

    cv::Mat Lx;
    cv::sepFilter2D(src, Lx, CV_64F, M, G);

    cv::Mat Ly;
    cv::sepFilter2D(src, Ly, CV_64F, G, M);

    cv::Mat FM = cv::abs(Lx) + cv::abs(Ly);

    double focusMeasure = cv::mean(FM).val[0];
    return focusMeasure;
}

// OpenCV port of 'LAPV' algorithm (Pech2000)
double varianceOfLaplacian(const cv::Mat& src)
{
    cv::Mat lap;
    cv::Laplacian(src, lap, CV_64F);

    cv::Scalar mu, sigma;
    cv::meanStdDev(lap, mu, sigma);

    double focusMeasure = sigma.val[0]*sigma.val[0];
    return focusMeasure;
}

// OpenCV port of 'TENG' algorithm (Krotkov86)
double tenengrad(const cv::Mat& src, int ksize)
{
    cv::Mat Gx, Gy;
    cv::Sobel(src, Gx, CV_64F, 1, 0, ksize);
    cv::Sobel(src, Gy, CV_64F, 0, 1, ksize);

    cv::Mat FM = Gx.mul(Gx) + Gy.mul(Gy);

    double focusMeasure = cv::mean(FM).val[0];
    return focusMeasure;
}

// OpenCV port of 'GLVN' algorithm (Santos97)
double normalizedGraylevelVariance(const cv::Mat& src)
{
    cv::Scalar mu, sigma;
    cv::meanStdDev(src, mu, sigma);

    double focusMeasure = (sigma.val[0]*sigma.val[0]) / mu.val[0];
    return focusMeasure;
}

Aucune garantie sur si oui ou non ces mesures sont le meilleur choix pour votre problème, mais si vous traquez les documents associés à ces mesures, ils peuvent vous donner plus de perspicacité. J'espère que vous trouverez le code utile! Je sais que j'ai fait.

Construire sur la réponse de Nike. Il est simple d'implémenter la méthode basée sur laplacian avec opencv:

short GetSharpness(char* data, unsigned int width, unsigned int height)
{
    // assumes that your image is already in planner yuv or 8 bit greyscale
    IplImage* in = cvCreateImage(cvSize(width,height),IPL_DEPTH_8U,1);
    IplImage* out = cvCreateImage(cvSize(width,height),IPL_DEPTH_16S,1);
    memcpy(in->imageData,data,width*height);

    // aperture size of 1 corresponds to the correct matrix
    cvLaplace(in, out, 1);

    short maxLap = -32767;
    short* imgData = (short*)out->imageData;
    for(int i =0;i<(out->imageSize/2);i++)
    {
        if(imgData[i] > maxLap) maxLap = imgData[i];
    }

    cvReleaseImage(&in);
    cvReleaseImage(&out);
    return maxLap;
}

Retournera un court indiquant la netteté maximale détectée, ce qui, d'après mes tests sur des échantillons du monde réel, est un très bon indicateur de si une caméra est mise au point ou non. Sans surprise, les valeurs normales dépendent de la scène mais Beaucoup moins que la méthode FFT qui doit être élevée d'un taux de faux positifs pour être utile dans mon application.

J'ai trouvé une solution totalement différente. J'avais besoin d'analyser les images vidéo pour trouver la plus nette de toutes les images (X). De cette façon, je détecterais le flou de mouvement et/ou les images floues.

J'ai fini par utiliser Canny Edge detection et j'ai obtenu de très très bons résultats avec presque tous les types de vidéo (avec la méthode de nikie, j'ai eu des problèmes avec les vidéos VHS numérisées et les vidéos entrelacées lourdes).

J'ai optimisé les performances en définissant une région d'intérêt image d'origine.

En Utilisant EmguCV:

//Convert image using Canny
using (Image<Gray, byte> imgCanny = imgOrig.Canny(225, 175))
{
    //Count the number of pixel representing an edge
    int nCountCanny = imgCanny.CountNonzero()[0];

    //Compute a sharpness grade:
    //< 1.5 = blurred, in movement
    //de 1.5 à 6 = acceptable
    //> 6 =stable, sharp
    double dSharpness = (nCountCanny * 1000.0 / (imgCanny.Cols * imgCanny.Rows));
}

Merci nikie pour cette excellente suggestion de Laplace. OpenCV docs m'a pointé dans la même direction: en utilisant python, cv2 (opencv 2.4.10) et numpy...

gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) numpy.max(cv2.convertScaleAbs(cv2.Laplacian(gray_image,3)))

Le résultat est compris entre 0 et 255. J'ai trouvé quelque chose sur 200ish est très au point, et par 100, c'est sensiblement flou. le max n'obtient jamais vraiment beaucoup moins de 20 même s'il est complètement flou.

Une façon que j'utilise actuellement mesure la propagation des bords dans l'image. Recherchez ce document:

@ARTICLE{Marziliano04perceptualblur,
    author = {Pina Marziliano and Frederic Dufaux and Stefan Winkler and Touradj Ebrahimi},
    title = {Perceptual blur and ringing metrics: Application to JPEG2000,” Signal Process},
    journal = {Image Commun},
    year = {2004},
    pages = {163--172} }

C'est généralement derrière un paywall mais j'ai vu des copies gratuites autour. Fondamentalement, ils localisent les bords verticaux dans une image, puis mesurent la largeur de ces bords. La moyenne de la largeur donne le résultat final de l'estimation du flou pour l'image. Les bords plus larges correspondent à des images floues, et vice versa.

Ce problème appartient au champ de image sans référence estimation de la qualité . Si vous regardez sur Google Scholar, vous obtiendrez beaucoup de références utiles.

Modifier

Voici un tracé des estimations de flou obtenues pour les 5 images dans le post de nikie. Des valeurs plus élevées correspondent à un plus grand flou. J'ai utilisé un filtre gaussien de taille fixe 11x11 et varié l'écart-type (en utilisant la commande convert d'imagemagick pour obtenir les images floues).

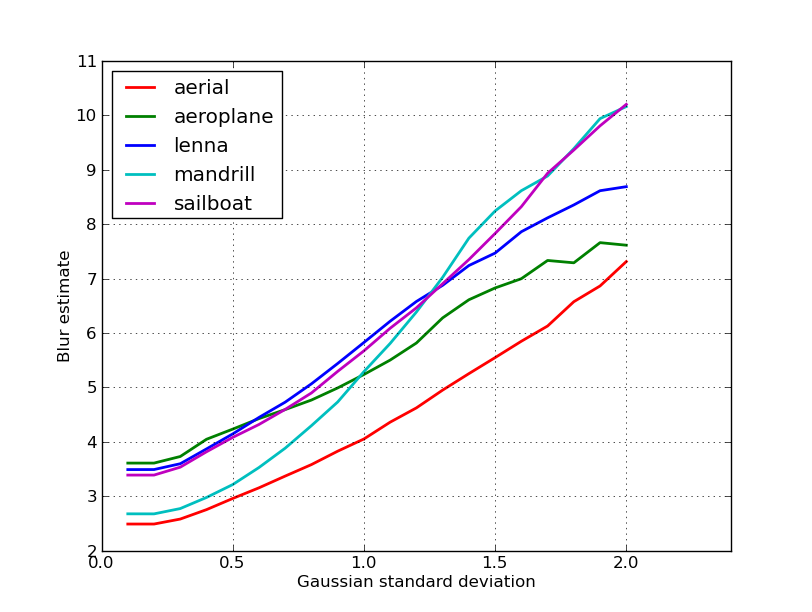
Si vous comparez des images de différentes tailles, n'oubliez pas de normaliser par la largeur de l'image, car les images plus grandes auront des bords plus larges.

Enfin, un problème important est de faire la distinction entre le flou artistique et le flou indésirable (causé par le manque de mise au point, la compression, le mouvement relatif du sujet à la caméra), mais cela dépasse les approches simples comme celle-ci. Pour un exemple de flou artistique, jetez un oeil à L'image de Lenna: le reflet de Lenna dans le miroir est flou, mais son visage est parfaitement au point. Cela contribue à un flou plus élevé estimation pour L'image de Lenna.

Les Réponses ci-dessus ont élucidé beaucoup de choses, mais je pense qu'il est utile de faire une distinction conceptuelle.

Que faire si vous prenez une image parfaitement mise au point d'une image floue?

Le problème de détection du flou n'est bien posé que lorsque vous avez une référence . Si vous devez concevoir, par exemple, un système de mise au point automatique, vous comparez une séquence d'images prises avec différents degrés de flou, ou de lissage, et vous essayez de trouver le point de flou minimum dans cet ensemble. Je en d'autres termes, vous devez croiser les différentes images en utilisant l'une des techniques illustrées ci-dessus (essentiellement-avec différents niveaux de raffinement possibles dans l'approche-à la recherche de l'image avec le contenu à haute fréquence le plus élevé).

J'ai essayé solution basée sur le filtre Laplacien de ce post. Il ne m'a pas aidé. Donc, j'ai essayé la solution à partir de ce post et c'était bon pour mon cas (mais c'est lent):

import cv2

image = cv2.imread("test.jpeg")
height, width = image.shape[:2]
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

def px(x, y):
    return int(gray[y, x])

sum = 0
for x in range(width-1):
    for y in range(height):
        sum += abs(px(x, y) - px(x+1, y))

L'image moins floue a une valeur maximale sum!

Vous pouvez également régler la vitesse et la précision en changeant l'étape, par exemple

Cette partie

for x in range(width - 1):

Vous pouvez remplacer par celui-ci

for x in range(0, width - 1, 10):

Le code Matlab de deux méthodes qui ont été publiées dans des revues de renom (Transactions IEEE sur le traitement D'Image) est disponible ici: https://ivulab.asu.edu/software

Vérifiez les algorithmes CPBDM et JNBM. Si vous vérifiez le code, il n'est pas très difficile d'être porté et, incidemment, il est basé sur la méthode de Marzialiano comme caractéristique de base.

Je l'ai implémenté utiliser fft dans matlab et vérifier l'histogramme de la moyenne de calcul fft et std mais aussi la fonction fit peut être faite

fa =  abs(fftshift(fft(sharp_img)));
fb = abs(fftshift(fft(blured_img)));

f1=20*log10(0.001+fa);
f2=20*log10(0.001+fb);

figure,imagesc(f1);title('org')
figure,imagesc(f2);title('blur')

figure,hist(f1(:),100);title('org')
figure,hist(f2(:),100);title('blur')

mf1=mean(f1(:));
mf2=mean(f2(:));

mfd1=median(f1(:));
mfd2=median(f2(:));

sf1=std(f1(:));
sf2=std(f2(:));

C'est ce que je fais dans Opencv pour détecter la qualité de mise au point dans une Région:

Mat grad;
int scale = 1;
int delta = 0;
int ddepth = CV_8U;
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
/// Gradient X
Sobel(matFromSensor, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT);
/// Gradient Y
Sobel(matFromSensor, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT);
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);
cv::Scalar mu, sigma;
cv::meanStdDev(grad, /* mean */ mu, /*stdev*/ sigma);
focusMeasure = mu.val[0] * mu.val[0];