Interprétation de L'algorithme de Dijkstra

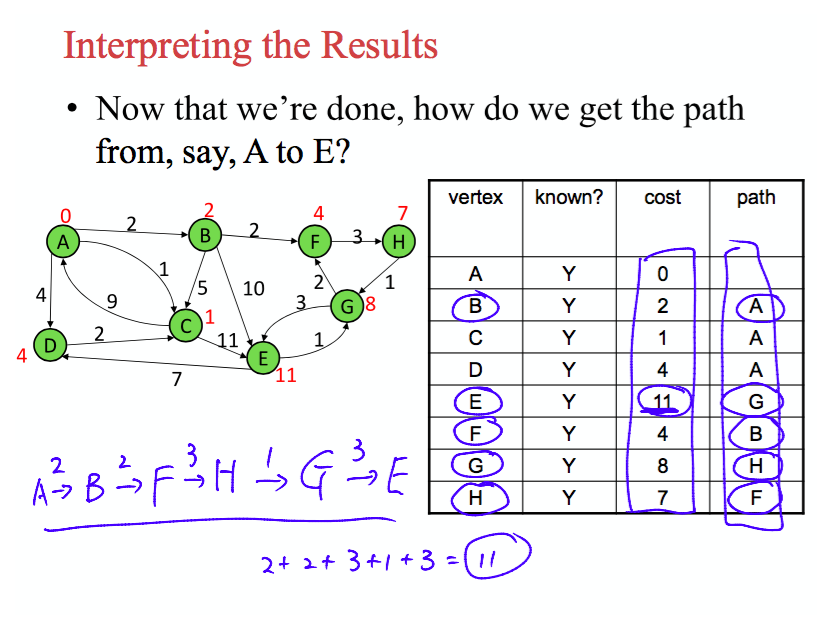
Graph

je comprends comment trouver le chemin le plus court du début à la fin comme expliqué par L'algorithme de Dijkstra, ce que je ne comprends pas est l'interprétation. Ici, à partir du graphique de l'image, l'ordre ajouté à mon ensemble connu de A à E est A,C,B,D,F,H,G,E ce que je ne comprends pas, c'est comment obtenir le chemin de A à E comme indiqué dans l'image (l'aspect mathématique)

12
demandé sur i_use_the_internet 2015-04-20 21:33:09

3 réponses

chaque noeud a un noeud parent. Quand vous atteignez 'E', vous regardez simplement son parent et ainsi de suite jusqu'à ce que vous trouviez 'A'. De cette façon, vous trouverez la liste dans l'ordre inverse. Inversez la liste pour trouver le chemin à partir de 'A''E'.

votre liste de parents sera 'E' 'G' 'H' 'F' 'B' 'A' si vous ajoutez dans l'ordre.

NOTE: le "noeud parent" est le noeud indiqué dans la colonne "Chemin" de la table

10
répondu Thellimist 2015-04-30 22:46:52

Envisager un minimum de file d'attente de priorité contenant les chemins à parcourir le chemin d'accès de priorité dans la file d'attente est le coût de la traversée des arêtes dans le chemin d'accès à partir de la racine jusqu'à et y compris ce bord. À chaque étape de l'algorithme, ouvrez le chemin le moins coûteux de la file d'attente et, en considérant chacun de ses bords incidents, prolongez le chemin avec ce bord incident et repoussez le nouveau chemin vers la file d'attente dans l'ordre de priorité. Répétez jusqu'à ce que le premier chemin atteint le destination.

Par exemple:

  1. Démarrer avec un vide la file d'attente <>
  2. Puis, à partir de la racine A, mettez tous les bords incidents (A->B, A->C et A->D avec un prix de 2, 1 et 4, respectivement) dans la file d'attente et par ordre de priorité: <(A->C,1),(A->B,2),(A->D,4)>
  3. Pop la priorité minimale chemin A->C à partir de l'avant de la file d'attente et d'examiner ensuite les bords de l'incident à la fin du chemin d'accès C et repousse ces chemins sur le la file d'attente (le maintien de l'ordre de priorité): <(A->B,2),(A->D,4),(A->C->A,10),(A->C->E,12)>
  4. Répéter, éclater la priorité minimale chemin A->B off et en étendant les chemins avec des arêtes incidentes: <(A->D,4),(A->B->F,4),(A->B->C,7),(A->C->A,10),(A->B->E,12),(A->C->E,12)>
  5. continuer... pop A->D et pousser plus arêtes incidentes: <(A->B->F,4),(A->D->C,6),(A->B->C,7),(A->C->A,10),(A->B->E,12),(A->C->E,12)>
  6. pop A->B->F et pousser plus arêtes incidentes: <(A->D->C,6),(A->B->C,7),(A->B->F->H,7),(A->C->A,10),(A->B->E,12),(A->C->E,12)>
  7. pop A->D->C - cependant, nous avons déjà atteint C avec un chemin de coût plus faible donc peut l'ignorer.
  8. pop A->B->C et ignorer il.
  9. pop A->B->F->H et pousser plus arêtes incidentes: <(A->B->F->H->G,8),(A->C->A,10),(A->B->E,12),(A->C->E,12)>
  10. pop A->B->F->H et pousser plus arêtes incidentes: <(A->B->F->H->G->F,10),(A->C->A,10),(A->B->F->H->G->E,11),(A->B->E,12),(A->C->E,12)>
  11. pop A->B->F->H->G->F et l'ignorer.
  12. pop A->C->A et l'ignorer.
  13. pop A->B->F->H->G->E et nous avons atteint l'objectif (avec un coût de 11)!
1
répondu MT0 2015-04-20 19:34:50

en commençant par le noeud de départ, un calcul de poids cumulatif est effectué lors de la traversée du graphe vers les noeuds disponibles. Le poids cumulatif d'un noeud à un noeud adjacent est comparé à n'importe quel résultat antérieur (c.-à-d., des traversées possibles à ce noeud). L'itinéraire le plus faible poids cumulé est ensuite choisi comme le "vainqueur". Le processus se répète jusqu'à ce qu'un chemin du début au noeud terminal soit trouvé et évalué comme étant le poids cumulatif le plus bas.

Donc dans l' exemple, vous avez indiqué:

  • ACE = 12
  • ADCE = 17
  • ABE = 12

ABFHGE est le seul chemin restant (dans le graphique dirigé) avec le plus faible poids cumulé de 11 (et aussi le plus long chemin) du début à la fin.

Comme vous calculer dès le départ que certains chemins semblent d'abord être plus courte (AC), mais que l'algorithme progresse ces choix sont abandonnés comme tous les chemins de A à E sont explorées.

0
répondu jhenderson2099 2015-04-20 19:25:29