Interpolation sur grille régulière en Python
j'ai eu du mal à intégrer les données pour les pixels "vides" dans ma matrice 2D. Fondamentalement, je comprends (mais pas profondément) les techniques d'interpolation telles que la pondération Inverse de la Distance, Krigging,Bicubic etc. Je ne connais pas exactement le point de départ (que ce soit dans l'énoncé du problème ou dans le cas de Python).
La définition du problème: J'ai une matrice MxN (grille régulière) dans laquelle chaque pixel représente une certaine valeur de mesure ( figure ci-dessous et les données utilisées dans cette figure estici). J'ai voulu interpoler les données pour "l'espace du point d'interrogation" (espace blanc qui se compose également de la même taille mais les pixels vides) des zones en utilisant les données existantes que j'ai comme pixels bleus.
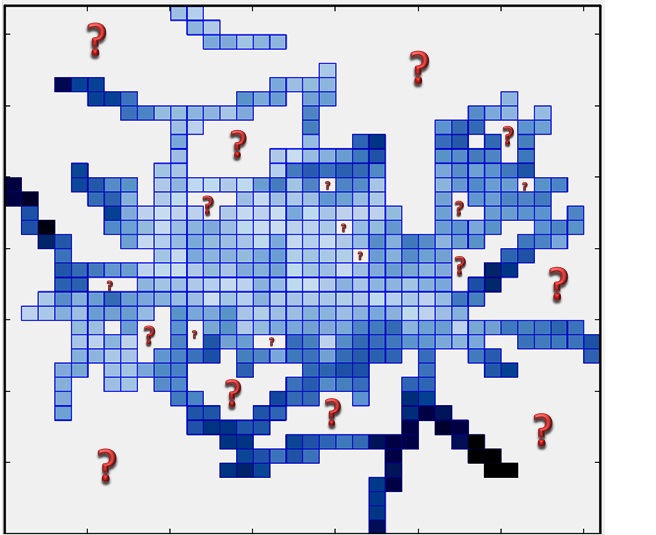
ma question:
1) Comment puis-je interpoler ces données. Est-ce que quelqu'un pourrait me donner un exemple simple (par exemple matrice 3x3) pour comprendre que clairement?
2) est-ce que quelqu'un pourrait me guider pour effectuer les étapes vers la solution dans L'environnement Python?
3) Comment puis-je comparer les techniques d'interpolation dans le sens de la précision en utilisant Python?
4) pensez-vous que c'est une bonne idée d'utiliser différents interpolation en fonction de la densité des données?
je vais apprécier vos réponses et suggestions.
1 réponses
ce qui est une solution raisonnable dépend en grande partie des questions auxquelles vous essayez de répondre avec les pixels interpolés -- attention emptor: extrapoler sur des données manquantes peut conduire à des réponses très trompeuses!
Fonction De Base Radiale Interpolation / Lissage Du Noyau
en termes de solutions pratiques disponibles en Python, une façon de remplir ces pixels serait d'utiliser L'implémentation par Scipy de l'interpolation de la fonction de base radiale (voir ici) qui est destiné au lissage/interpolation de données dispersées.
compte tenu de votre matrice M sous-jacents et les 1D coordonner les tableaux r et c (tels que M.shape == (r.size, c.size)), où les entrées manquantes de M sont définies pour nan, cela semble fonctionner assez bien avec un noyau RBF linéaire comme suit:
import numpy as np
import scipy.interpolate as interpolate
with open('measurement.txt') as fh:
M = np.vstack(map(float, r.split(' ')) for r in fh.read().splitlines())
r = np.linspace(0, 1, M.shape[0])
c = np.linspace(0, 1, M.shape[1])
rr, cc = np.meshgrid(r, c)
vals = ~np.isnan(M)
f = interpolate.Rbf(rr[vals], cc[vals], M[vals], function='linear')
interpolated = f(rr, cc)
ceci produit l'interpolation suivante des données que vous avez liées ci-dessus, qui bien que d'apparence raisonnable, ne fait ressortir comment défavorable le rapport entre les échantillons manquants et les données réelles est de:
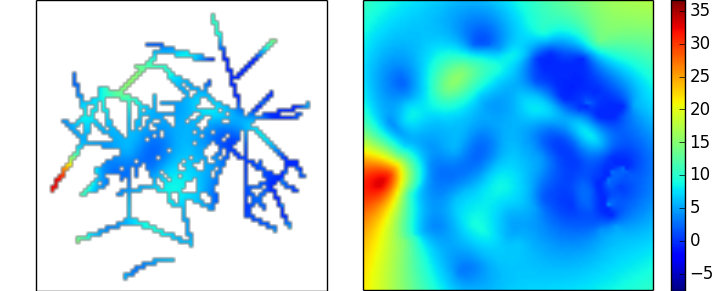
Processus Gaussien Régression / Krigging
l'interpolation Krigging est disponible via le Régression Gaussienne Du Processus implémentation (elle-même basée sur la boîte à outils DACE Kriging pour Matlab) dans la bibliothèque scikit-learn. Ceci pourrait être invoqué comme suit:
from sklearn.gaussian_process import GaussianProcess
gp = GaussianProcess(theta0=0.1, thetaL=.001, thetaU=1., nugget=0.01)
gp.fit(X=np.column_stack([rr[vals],cc[vals]]), y=M[vals])
rr_cc_as_cols = np.column_stack([rr.flatten(), cc.flatten()])
interpolated = gp.predict(rr_cc_as_cols).reshape(M.shape)
on obtient une interpolation très similaire à celle du Radial Exemple de fonction de base ci-dessus. Dans les deux cas, il y a beaucoup de paramètres à explorer - le choix de ceux-ci dépend largement des hypothèses que vous pouvez faire au sujet des données. (Un des avantages du noyau linéaire utilisé dans L'exemple RBF ci-dessus est qu'il n'a pas de paramètres libres)
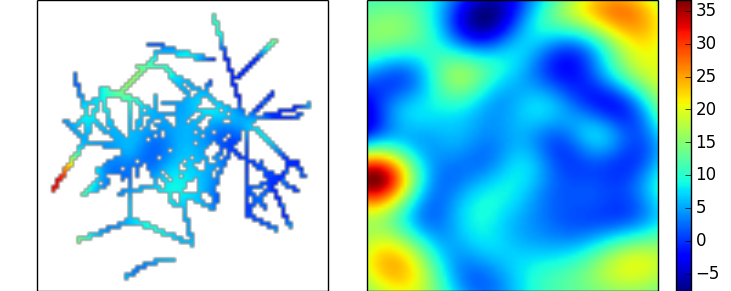
Inpainting
en conclusion, Unvisuellement motivé la solution serait D'utiliser Opencv's inpainting la fonctionnalité, bien que cela suppose des tableaux de 8 bits (0 - 255), et n'a pas une interprétation mathématique simple.