En R, traçant les effets aléatoires de lmer (paquet lme4) à l'aide de qqmath ou dotplot: comment les rendre fantaisistes?

la fonction qqmath fait de grands tracés caterpillaires d'effets aléatoires en utilisant la sortie du paquet lmer. C'est, qqmath est grande au tracé de la intercepte à partir d'un modèle hiérarchique avec leurs erreurs autour de l'estimation ponctuelle. Vous trouverez ci-dessous un exemple des fonctions lmer et qqmath en utilisant les données intégrées dans le paquet lme4 appelé Dyestuff. Le code produira le modèle hiérarchique et un joli tracé en utilisant la fonction ggmath.

library("lme4")
data(package = "lme4")

# Dyestuff 
# a balanced one-way classiï¬cation of Yield 
# from samples produced from six Batches

summary(Dyestuff)             

# Batch is an example of a random effect
# Fit 1-way random effects linear model
fit1 <- lmer(Yield ~ 1 + (1|Batch), Dyestuff) 
summary(fit1)
coef(fit1) #intercept for each level in Batch 

# qqplot of the random effects with their variances
qqmath(ranef(fit1, postVar = TRUE), strip = FALSE)$Batch

La dernière ligne de code produit une très belle parcelle de chaque intercepter l'erreur autour de chaque estimation. Mais le formatage de la fonction qqmath semble être très difficile, et j'ai eu du mal à formater l'intrigue. J'ai posé quelques questions auxquelles je ne peux pas répondre et dont je pense que d'autres pourraient également tirer profit s'ils utilisent la combinaison lmer/qqmath:

  1. y a-t-il un moyen de prendre la fonction qqmath ci-dessus et d'en ajouter quelques-unes options, telles que, rendre certains points vides par opposition à remplis, ou différentes couleurs pour différents points? Par exemple,Pouvez-vous faire remplir les points pour A, B et C de la variable Batch, mais vider le reste des points?
  2. est - il possible d'ajouter des étiquettes d'axes pour chaque point (peut-être le long de la en haut ou à droite de l'axe y, par exemple)?
  3. Mes données ont des en plus proche de 45 intercepte, de sorte qu'il est possible d'ajouter espacement entre les étiquettes pour qu'elles ne se croisent pas? Principalement, je suis intéressé à distinguer / étiqueter entre les points sur le graphique, qui semble encombrant / impossible dans la fonction ggmath.

jusqu'à présent, l'ajout d'une option supplémentaire dans la fonction qqmath produit des erreurs où je n'obtiendrais pas d'erreurs si c'était un tracé standard, donc je suis perdu.

en outre, si vous pensez qu'il y a un meilleur paquet/fonction pour tracer des intercepts à partir de la sortie lmer, j'aimerais l'entendre! (par exemple, Pouvez-vous faire les points 1-3 en utilisant dotplot?)

Merci.

EDIT: je suis aussi ouvert à un dotplot alternatif s'il peut être raisonnablement formaté. J'aime juste l'apparence d'un complot de ggmath, donc je commence par une question à ce sujet.

31
demandé sur Didzis Elferts 2012-12-13 00:20:21

3 réponses

Une possibilité est d'utiliser la bibliothèque ggplot2 dessiner graphique similaire et ensuite vous pouvez régler l'apparence de votre parcelle de terrain.

tout d'Abord, ranef l'objet est sauvegardé en tant que randoms. Puis les variances des intercepts sont sauvegardées dans l'objet qq.

randoms<-ranef(fit1, postVar = TRUE)
qq <- attr(ranef(fit1, postVar = TRUE)[[1]], "postVar")

Objet rand.interc contient juste des interceptions aléatoires avec des noms de niveaux.

rand.interc<-randoms$Batch

tous les objets mis dans une base de données. Pour les intervalles d'erreur sd.interc est calculé comme 2 fois racine carrée de écart.

df<-data.frame(Intercepts=randoms$Batch[,1],
              sd.interc=2*sqrt(qq[,,1:length(qq)]),
              lev.names=rownames(rand.interc))

si vous avez besoin que les interceptions soient ordonnées dans la parcelle en fonction de la valeur alors lev.names devrait être réorganisé. Cette ligne peut être ignorée si intercepte doit être ordonnée par nom.

df$lev.names<-factor(df$lev.names,levels=df$lev.names[order(df$Intercepts)])

ce code produit un tracé. Maintenant, les points différeront de shape selon les niveaux de facteurs.

library(ggplot2)
p <- ggplot(df,aes(lev.names,Intercepts,shape=lev.names))

#Added horizontal line at y=0, error bars to points and points with size two
p <- p + geom_hline(yintercept=0) +geom_errorbar(aes(ymin=Intercepts-sd.interc, ymax=Intercepts+sd.interc), width=0,color="black") + geom_point(aes(size=2)) 

#Removed legends and with scale_shape_manual point shapes set to 1 and 16
p <- p + guides(size=FALSE,shape=FALSE) + scale_shape_manual(values=c(1,1,1,16,16,16))

#Changed appearance of plot (black and white theme) and x and y axis labels
p <- p + theme_bw() + xlab("Levels") + ylab("")

#Final adjustments of plot
p <- p + theme(axis.text.x=element_text(size=rel(1.2)),
               axis.title.x=element_text(size=rel(1.3)),
               axis.text.y=element_text(size=rel(1.2)),
               panel.grid.minor=element_blank(),
               panel.grid.major.x=element_blank())

#To put levels on y axis you just need to use coord_flip()
p <- p+ coord_flip()
print(p)

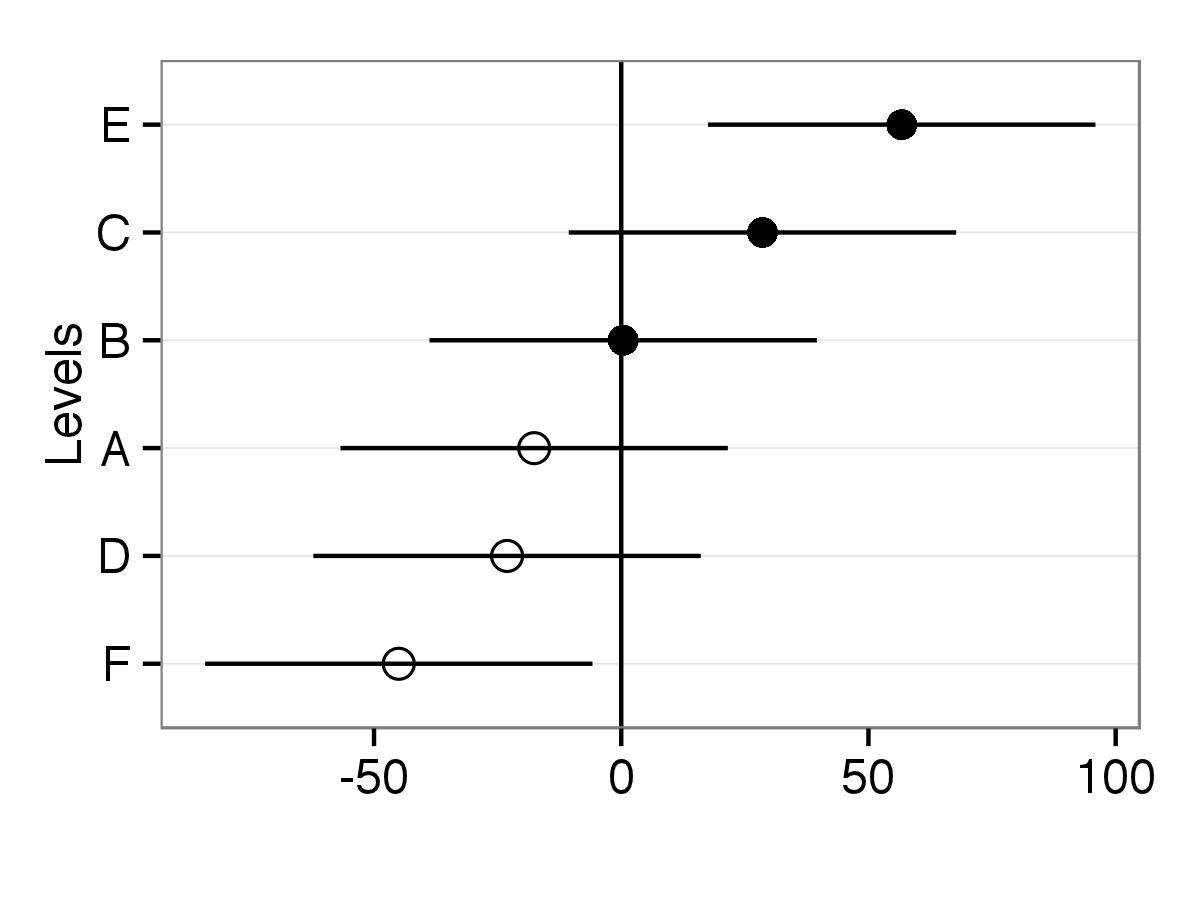
enter image description here

33
répondu Didzis Elferts 2012-12-18 06:13:39

la réponse de Didzis est géniale! Juste pour envelopper un peu, je l'ai mis dans sa propre fonction qui se comporte un peu comme qqmath.ranef.mer() et dotplot.ranef.mer(). En plus de la réponse de Didzis, il traite aussi des modèles avec des effets aléatoires corrélés multiples (comme qqmath() et dotplot() le faire). Comparaison qqmath():

require(lme4)                            ## for lmer(), sleepstudy
require(lattice)                         ## for dotplot()
fit <- lmer(Reaction ~ Days + (Days|Subject), sleepstudy)
ggCaterpillar(ranef(fit, condVar=TRUE))  ## using ggplot2
qqmath(ranef(fit, condVar=TRUE))         ## for comparison

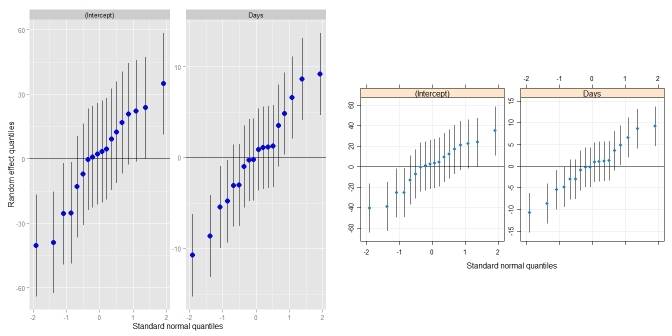
enter image description here

Comparaison dotplot():

ggCaterpillar(ranef(fit, condVar=TRUE), QQ=FALSE)
dotplot(ranef(fit, condVar=TRUE))

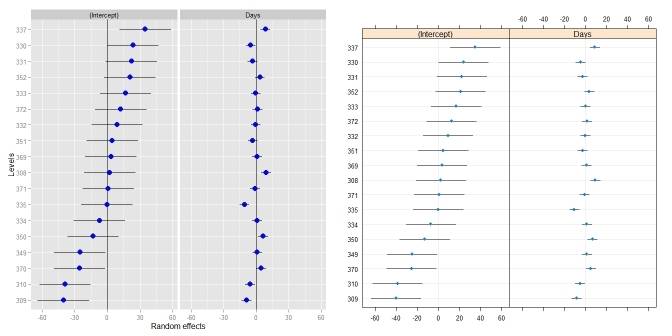
enter image description here

Parfois, il peut être utile d'avoir différentes échelles pour les effets aléatoires - quelque chose qui dotplot() applique. Quand j'ai essayé de détendre ceci, j'ai dû changer le facetting (voir ceci réponse).

ggCaterpillar(ranef(fit, condVar=TRUE), QQ=FALSE, likeDotplot=FALSE)

enter image description here

## re = object of class ranef.mer
ggCaterpillar <- function(re, QQ=TRUE, likeDotplot=TRUE) {
    require(ggplot2)
    f <- function(x) {
        pv   <- attr(x, "postVar")
        cols <- 1:(dim(pv)[1])
        se   <- unlist(lapply(cols, function(i) sqrt(pv[i, i, ])))
        ord  <- unlist(lapply(x, order)) + rep((0:(ncol(x) - 1)) * nrow(x), each=nrow(x))
        pDf  <- data.frame(y=unlist(x)[ord],
                           ci=1.96*se[ord],
                           nQQ=rep(qnorm(ppoints(nrow(x))), ncol(x)),
                           ID=factor(rep(rownames(x), ncol(x))[ord], levels=rownames(x)[ord]),
                           ind=gl(ncol(x), nrow(x), labels=names(x)))

        if(QQ) {  ## normal QQ-plot
            p <- ggplot(pDf, aes(nQQ, y))
            p <- p + facet_wrap(~ ind, scales="free")
            p <- p + xlab("Standard normal quantiles") + ylab("Random effect quantiles")
        } else {  ## caterpillar dotplot
            p <- ggplot(pDf, aes(ID, y)) + coord_flip()
            if(likeDotplot) {  ## imitate dotplot() -> same scales for random effects
                p <- p + facet_wrap(~ ind)
            } else {           ## different scales for random effects
                p <- p + facet_grid(ind ~ ., scales="free_y")
            }
            p <- p + xlab("Levels") + ylab("Random effects")
        }

        p <- p + theme(legend.position="none")
        p <- p + geom_hline(yintercept=0)
        p <- p + geom_errorbar(aes(ymin=y-ci, ymax=y+ci), width=0, colour="black")
        p <- p + geom_point(aes(size=1.2), colour="blue") 
        return(p)
    }

    lapply(re, f)
}
35
répondu caracal 2018-05-14 07:24:18

une autre façon de faire ceci est d'extraire des valeurs simulées de la distribution de chacun des effets aléatoires et de les tracer. À l'aide de la merTools package, il est possible d'obtenir facilement les simulations à partir d'un lmer ou glmer objet, et de l'intrigue. 

library(lme4); library(merTools)       ## for lmer(), sleepstudy
fit <- lmer(Reaction ~ Days + (Days|Subject), sleepstudy)
randoms <- REsim(fit, n.sims = 500)

randoms est maintenant un objet qui ressemble à:

head(randoms)
groupFctr groupID        term       mean     median       sd
1   Subject     308 (Intercept)   3.083375   2.214805 14.79050
2   Subject     309 (Intercept) -39.382557 -38.607697 12.68987
3   Subject     310 (Intercept) -37.314979 -38.107747 12.53729
4   Subject     330 (Intercept)  22.234687  21.048882 11.51082
5   Subject     331 (Intercept)  21.418040  21.122913 13.17926
6   Subject     332 (Intercept)  11.371621  12.238580 12.65172

Il fournit le nom du groupement facteur, le niveau du facteur, nous obtenons une estimation, le terme dans le modèle, et la moyenne, médiane et écart-type des valeurs simulées. Nous pouvons l'utiliser pour générer un tracé caterpillar similaire à ceux ci-dessus:

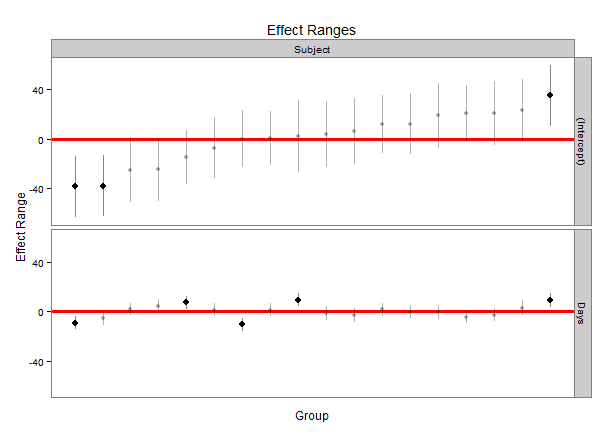
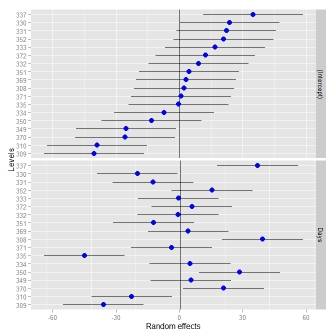
plotREsim(randoms)

qui produit:

A caterpillar plot of random effects

une caractéristique intéressante est que les valeurs qui ont un intervalle de confiance qui ne chevauche pas zéro sont surlignées en noir. Vous pouvez modifier la largeur de l'intervalle en utilisant le level paramètre plotREsim faire plus ou moins confiance intervalles en fonction de vos besoins.

12
répondu jknowles 2015-08-13 14:55:29