Dans L'ordre successeur dans L'Arbre de recherche binaire
avec un noeud dans un BST, comment trouve-t-on la touche supérieure suivante?
16 réponses
la manière générale dépend si vous avez un lien parent dans vos noeuds ou non.
si vous stockez le lien parent
puis vous choisissez:
- l'enfant le plus à gauche de l'enfant droit, si votre noeud actuel a un enfant droit. Si l'enfant de droite n'a pas d'enfant de gauche, l'enfant de droite est votre successeur.
- naviguez vers le haut des noeuds ancêtre parent, et quand vous trouvez un parent dont le gauche l'enfant est le noeud où vous êtes actuellement, le parent est le successeur ordonné de votre noeud d'origine.
si vous avez un enfant légitime, faites cette approche (cas 1 ci-dessus):
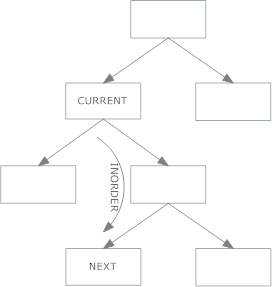
si vous n'avez pas d'enfant légitime, faites cette approche (cas 2 ci-dessus):
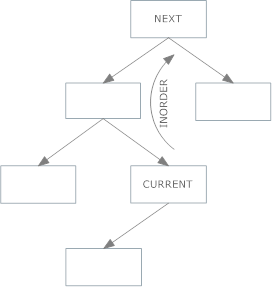
si vous ne stockez pas le lien parent
puis vous besoin d'exécuter un balayage complet de l'arbre, en gardant la trace des noeuds, généralement avec une pile, de sorte que vous avez les informations nécessaires pour faire fondamentalement la même chose que la première méthode qui s'est fiée sur le lien parent.
code Python pour le Lasse réponse :
def findNext(node):
if node.rightChild != None:
return findMostLeft(node.rightChild)
else:
parent = node.parent
while parent != None:
if parent.leftChild == node:
break
node = parent
parent = node.parent
return parent
découvrez ici : Afinde Successeur dans un Arbre de Recherche Binaire
en arbre binaire, Inorder successeur d'un le nœud est le nœud suivant Afinde la traversée de l'Arbre Binaire. Afinde Le successeur est nul pour le dernier noeud dans Inoorder traversée. Dans La Recherche Binaire Arbre, Inorder successeur d'une entrée nœud peut également être défini comme le nœud avec la plus petite clé plus grande que la la clé du nœud d'entrée.
Voici une implémentation sans liens parents ou structures intermédiaires (comme une pile). Cette fonction de successeur en ordre est un peu différente de ce que la plupart pourraient être à la recherche pour puisqu'elle opère sur la clé par opposition au noeud. Aussi, il sera de trouver un successeur d'une clé, même si elle n'est pas présente dans l'arbre. Pas trop difficile de changer si vous aviez besoin, cependant.
public class Node<T extends Comparable<T>> {
private T data;
private Node<T> left;
private Node<T> right;
public Node(T data, Node<T> left, Node<T> right) {
this.data = data;
this.left = left;
this.right = right;
}
/*
* Returns the left-most node of the current node. If there is no left child, the current node is the left-most.
*/
private Node<T> getLeftMost() {
Node<T> curr = this;
while(curr.left != null) curr = curr.left;
return curr;
}
/*
* Returns the right-most node of the current node. If there is no right child, the current node is the right-most.
*/
private Node<T> getRightMost() {
Node<T> curr = this;
while(curr.right != null) curr = curr.right;
return curr;
}
/**
* Returns the in-order successor of the specified key.
* @param key The key.
* @return
*/
public T getSuccessor(T key) {
Node<T> curr = this;
T successor = null;
while(curr != null) {
// If this.data < key, search to the right.
if(curr.data.compareTo(key) < 0 && curr.right != null) {
curr = curr.right;
}
// If this.data > key, search to the left.
else if(curr.data.compareTo(key) > 0) {
// If the right-most on the left side has bigger than the key, search left.
if(curr.left != null && curr.left.getRightMost().data.compareTo(key) > 0) {
curr = curr.left;
}
// If there's no left, or the right-most on the left branch is smaller than the key, we're at the successor.
else {
successor = curr.data;
curr = null;
}
}
// this.data == key...
else {
// so get the right-most data.
if(curr.right != null) {
successor = curr.right.getLeftMost().data;
}
// there is no successor.
else {
successor = null;
}
curr = null;
}
}
return successor;
}
public static void main(String[] args) {
Node<Integer> one, three, five, seven, two, six, four;
one = new Node<Integer>(Integer.valueOf(1), null, null);
three = new Node<Integer>(Integer.valueOf(3), null, null);
five = new Node<Integer>(Integer.valueOf(5), null, null);
seven = new Node<Integer>(Integer.valueOf(7), null, null);
two = new Node<Integer>(Integer.valueOf(2), one, three);
six = new Node<Integer>(Integer.valueOf(6), five, seven);
four = new Node<Integer>(Integer.valueOf(4), two, six);
Node<Integer> head = four;
for(int i = 0; i <= 7; i++) {
System.out.println(head.getSuccessor(i));
}
}
}
avec L'Arbre de recherche binaire, l'algorithme pour trouver le prochain noeud le plus haut d'un noeud donné est essentiellement de trouver le noeud le plus bas du sous-arbre droit de ce noeud.
l'algorithme peut simplement être:
- démarrer avec l'enfant droit du noeud donné (en faire le noeud courant temporaire)
- si le noeud courant n'a pas d'enfant gauche, c'est le prochain noeud le plus haut.
- si le noeud courant a un enfant de gauche, faites-en le noeud courant.
répétez 2 et 3 jusqu'à ce que nous trouvions le prochain noeud le plus haut.
C++ solution en supposant que les Nœuds ont de gauche, de droite, et parent pointeurs:
cela illustre la fonction Node* getNextNodeInOrder(Node) qui renvoie la touche suivante de l'arbre de recherche binaire dans l'ordre.
#include <cstdlib>
#include <iostream>
using namespace std;
struct Node{
int data;
Node *parent;
Node *left, *right;
};
Node *createNode(int data){
Node *node = new Node();
node->data = data;
node->left = node->right = NULL;
return node;
}
Node* getFirstRightParent(Node *node){
if (node->parent == NULL)
return NULL;
while (node->parent != NULL && node->parent->left != node){
node = node->parent;
}
return node->parent;
}
Node* getLeftMostRightChild(Node *node){
node = node->right;
while (node->left != NULL){
node = node->left;
}
return node;
}
Node *getNextNodeInOrder(Node *node){
//if you pass in the last Node this will return NULL
if (node->right != NULL)
return getLeftMostRightChild(node);
else
return getFirstRightParent(node);
}
void inOrderPrint(Node *root)
{
if (root->left != NULL) inOrderPrint(root->left);
cout << root->data << " ";
if (root->right != NULL) inOrderPrint(root->right);
}
int main(int argc, char** argv) {
//Purpose of this program is to demonstrate the function getNextNodeInOrder
//of a binary tree in-order. Below the tree is listed with the order
//of the items in-order. 1 is the beginning, 11 is the end. If you
//pass in the node 4, getNextNode returns the node for 5, the next in the
//sequence.
//test tree:
//
// 4
// / \
// 2 11
// / \ /
// 1 3 10
// /
// 5
// \
// 6
// \
// 8
// / \
// 7 9
Node *root = createNode(4);
root->parent = NULL;
root->left = createNode(2);
root->left->parent = root;
root->right = createNode(11);
root->right->parent = root;
root->left->left = createNode(1);
root->left->left->parent = root->left;
root->right->left = createNode(10);
root->right->left->parent = root->right;
root->left->right = createNode(3);
root->left->right->parent = root->left;
root->right->left->left = createNode(5);
root->right->left->left->parent = root->right->left;
root->right->left->left->right = createNode(6);
root->right->left->left->right->parent = root->right->left->left;
root->right->left->left->right->right = createNode(8);
root->right->left->left->right->right->parent =
root->right->left->left->right;
root->right->left->left->right->right->left = createNode(7);
root->right->left->left->right->right->left->parent =
root->right->left->left->right->right;
root->right->left->left->right->right->right = createNode(9);
root->right->left->left->right->right->right->parent =
root->right->left->left->right->right;
inOrderPrint(root);
//UNIT TESTING FOLLOWS
cout << endl << "unit tests: " << endl;
if (getNextNodeInOrder(root)->data != 5)
cout << "failed01" << endl;
else
cout << "passed01" << endl;
if (getNextNodeInOrder(root->right) != NULL)
cout << "failed02" << endl;
else
cout << "passed02" << endl;
if (getNextNodeInOrder(root->right->left)->data != 11)
cout << "failed03" << endl;
else
cout << "passed03" << endl;
if (getNextNodeInOrder(root->left)->data != 3)
cout << "failed04" << endl;
else
cout << "passed04" << endl;
if (getNextNodeInOrder(root->left->left)->data != 2)
cout << "failed05" << endl;
else
cout << "passed05" << endl;
if (getNextNodeInOrder(root->left->right)->data != 4)
cout << "failed06" << endl;
else
cout << "passed06" << endl;
if (getNextNodeInOrder(root->right->left->left)->data != 6)
cout << "failed07" << endl;
else
cout << "passed07" << endl;
if (getNextNodeInOrder(root->right->left->left->right)->data != 7)
cout << "failed08 it came up with: " <<
getNextNodeInOrder(root->right->left->left->right)->data << endl;
else
cout << "passed08" << endl;
if (getNextNodeInOrder(root->right->left->left->right->right)->data != 9)
cout << "failed09 it came up with: "
<< getNextNodeInOrder(root->right->left->left->right->right)->data
<< endl;
else
cout << "passed09" << endl;
return 0;
}
qui imprime:
1 2 3 4 5 6 7 8 9 10 11
unit tests:
passed01
passed02
passed03
passed04
passed05
passed06
passed07
passed08
passed09
si nous effectuons une traversée dans l'ordre, Nous visitons le sous-arbre de gauche, puis le noeud racine et finalement le sous-arbre de droite pour chaque noeud de l'arbre. Effectuer une traversée dans l'ordre nous donnera les clés d'un arbre de recherche binaire dans l'ordre ascendant, donc quand nous nous référons à récupérer le successeur dans l'ordre d'un noeud appartenant à un arbre de recherche binaire nous voulons dire ce qui serait le prochain noeud dans la séquence à partir du noeud donné.
disons que nous avons un noeud R et nous voulons son dans afin successeur, nous aurions les cas suivants.
[1] la racine R a un noeud droit, donc tout ce que nous avons à faire est de traverser à gauche le plus de noeud de R->droite.
[2] la racine R n'a pas de noeud droit, dans ce cas nous traversons l'arbre en suivant les liens parent jusqu'à ce que le noeud R soit un enfant gauche de son parent, lorsque cela se produit nous avons le noeud parent P comme successeur dans l'ordre.
[3] nous sommes à l'extrémité droite du noeud de l'arbre, dans ce cas il n'y a pas de successeur dans l'ordre.
la mise en œuvre est basée sur la définition suivante du noeud
class node
{
private:
node* left;
node* right;
node* parent
int data;
public:
//public interface not shown, these are just setters and getters
.......
};
//go up the tree until we have our root node a left child of its parent
node* getParent(node* root)
{
if(root->parent == NULL)
return NULL;
if(root->parent->left == root)
return root->parent;
else
return getParent(root->parent);
}
node* getLeftMostNode(node* root)
{
if(root == NULL)
return NULL;
node* left = getLeftMostNode(root->left);
if(left)
return left;
return root;
}
//return the in order successor if there is one.
//parameters - root, the node whose in order successor we are 'searching' for
node* getInOrderSucc(node* root)
{
//no tree, therefore no successor
if(root == NULL)
return NULL;
//if we have a right tree, get its left most node
if(root->right)
return getLeftMostNode(root->right);
else
//bubble up so the root node becomes the left child of its
//parent, the parent will be the inorder successor.
return getParent(root);
}
nous n'avons pas besoin de lien parent ou de pile pour trouver le successeur en ordre dans O(log n) (en supposant un arbre équilibré). Conservez une variable temporaire avec la valeur la plus récente rencontrée dans l'ordre transversal qui est plus grande que la clé. si inorder traversal constate que le noeud n'a pas d'enfant droit, alors ce sera le successeur inorder. autrement, le descendant le plus à gauche de l'enfant droit.
vous pouvez lire des informations supplémentaires ici (Lung Russe)
Node next(Node x)
if x.right != null
return minimum(x.right)
y = x.parent
while y != null and x == y.right
x = y
y = y.parent
return y
Node prev(Node x)
if x.left != null
return maximum(x.left)
y = x.parent
while y != null and x == y.left
x = y
y = y.parent
return y
ces réponses me semblent trop compliquées. Nous n'avons vraiment pas besoin de pointeurs parent ou de structures de données auxiliaires comme une pile. Tout ce que nous devons faire est de parcourir l'arborescence de la racine dans l'ordre, de définir un indicateur dès que nous trouvons la cible nœud et le nœud suivant dans l'arbre que nous avons visite sera l', afin successeur du nœud. Voici une routine rapide et sale que j'ai écrite.
Node* FindNextInorderSuccessor(Node* root, int target, bool& done)
{
if (!root)
return NULL;
// go left
Node* result = FindNextInorderSuccessor(root->left, target, done);
if (result)
return result;
// visit
if (done)
{
// flag is set, this must be our in-order successor node
return root;
}
else
{
if (root->value == target)
{
// found target node, set flag so that we stop at next node
done = true;
}
}
// go right
return FindNextInorderSuccessor(root->right, target, done);
}
solution JavaScript - Si le noeud donné a un noeud droit, alors retourner le plus petit noeud dans le sous-arbre droit - Si non, alors il y a 2 possibilités: - Le noeud donné est un enfant gauche du noeud parent. Si c'est le cas, retournez le noeud parent. Autrement, le noeud donné est un enfant droit du noeud parent. Si c'est le cas, retournez l'enfant droit du noeud parent
function nextNode(node) {
var nextLargest = null;
if (node.right != null) {
// Return the smallest item in the right subtree
nextLargest = node.right;
while (nextLargest.left !== null) {
nextLargest = nextLargest.left;
}
return nextLargest;
} else {
// Node is the left child of the parent
if (node === node.parent.left) return node.parent;
// Node is the right child of the parent
nextLargest = node.parent;
while (nextLargest.parent !== null && nextLargest !== nextLargest.parent.left) {
nextLargest = nextLargest.parent
}
return nextLargest.parent;
}
}
cela en Java
TreeNode getSuccessor(TreeNode treeNode) {
if (treeNode.right != null) {
return getLeftMostChild(treeNode.right);
} else {
TreeNode p = treeNode.parent;
while (p != null && treeNode == p.right) { // traverse upwards until there is no parent (at the last node of BST and when current treeNode is still the parent's right child
treeNode = p;
p = p.parent; // traverse upwards
}
return p; // returns the parent node
}
}
TreeNode getLeftMostChild(TreeNode treeNode) {
if (treeNode.left == null) {
return treeNode;
} else {
return getLeftMostChild(treeNode.left);
}
}
on peut diviser cela en 3 cas:
-
si le noeud est un parent: dans ce cas, nous trouvons s'il a un noeud droit et traverse à l'enfant le plus à gauche du noeud droit. Dans le cas où le noeud droit n'a pas d'enfants alors le noeud droit est son successeur d'ordre. S'il n'y a pas de noeud droit, nous devons remonter l'arbre pour trouver le successeur.
-
si le noeud est un enfant gauche: dans ce cas, le parent est le afinde successeur.
-
si le noeud (appelé x) est un enfant droit (de son parent immédiat): nous traversons l'arbre jusqu'à ce que nous trouvions un noeud dont le sous-arbre de gauche a X.
cas extrême: si le noeud est le noeud de coin le plus à droite, il n'y a pas de successeur d'ordre.
chaque "tutoriel" que j'ai vérifié sur google et toutes les réponses dans ce thread utilise la logique suivante: " si le noeud n'a pas un enfant droit alors son successeur dans l'ordre sera l'un de ses ancêtres. Utiliser parent link continuer à voyager jusqu'à ce que vous obtenez le noeud qui est l'enfant gauche de son parent. Alors ce noeud parent sera le successeur dans l'ordre. "
c'est la même chose que de penser " si mon parent est plus grand que moi, alors Je suis l'enfant gauche " (propriété d'un arbre de recherche binaire). Cela signifie que vous pouvez simplement remonter la chaîne parent jusqu'à ce que la propriété ci-dessus soit vraie. Ce qui, à mon avis, se traduit par un code plus élégant.
je suppose que la raison pour laquelle tout le monde vérifie " suis-je l'enfant de gauche "en regardant les branches au lieu des valeurs dans le chemin de code qui utilise les liens de parent vient de la logique" d'emprunt " de l'algorithme de non-lien à parent.
également à partir du code inclus ci-dessous, nous pouvons voir qu'il y a pas besoin de structure de données de pile comme suggéré par d'autres réponses.
ci-dessous est une fonction C++ simple qui fonctionne pour les deux cas d'utilisation (avec et sans utiliser le lien vers parent).
Node* nextInOrder(const Node *node, bool useParentLink) const
{
if (!node)
return nullptr;
// when has a right sub-tree
if (node->right) {
// get left-most node from the right sub-tree
node = node->right;
while (node->left)
node = node->left;
return node;
}
// when does not have a right sub-tree
if (useParentLink) {
Node *parent = node->parent;
while (parent) {
if (parent->value > node->value)
return parent;
parent = parent->parent;
}
return nullptr;
} else {
Node *nextInOrder = nullptr;
// 'root' is a class member pointing to the root of the tree
Node *current = root;
while (current != node) {
if (node->value < current->value) {
nextInOrder = current;
current = current->left;
} else {
current = current->right;
}
}
return nextInOrder;
}
}
Node* previousInOrder(const Node *node, bool useParentLink) const
{
if (!node)
return nullptr;
// when has a left sub-tree
if (node->left) {
// get right-most node from the left sub-tree
node = node->left;
while (node->right)
node = node->right;
return node;
}
// when does not have a left sub-tree
if (useParentLink) {
Node *parent = node->parent;
while (parent) {
if (parent->value < node->value)
return parent;
parent = parent->parent;
}
return nullptr;
} else {
Node *prevInOrder = nullptr;
// 'root' is a class member pointing to the root of the tree
Node *current = root;
while (current != node) {
if (node->value < current->value) {
current = current->left;
} else {
prevInOrder = current;
current = current->right;
}
}
return prevInOrder;
}
}
C# de mise en œuvre (Non récursif!) pour trouver le "prochain" nœud d'un nœud dans un arbre de recherche binaire, où chaque nœud a un lien vers son parent.
public static Node WhoIsNextInOrder(Node root, Node node)
{
if (node.Right != null)
{
return GetLeftMost(node.Right);
}
else
{
Node p = new Node(null,null,-1);
Node Next = new Node(null, null, -1);
bool found = false;
p = FindParent(root, node);
while (found == false)
{
if (p.Left == node) { Next = p; return Next; }
node = p;
p = FindParent(root, node);
}
return Next;
}
}
public static Node FindParent(Node root, Node node)
{
if (root == null || node == null)
{
return null;
}
else if ( (root.Right != null && root.Right.Value == node.Value) || (root.Left != null && root.Left.Value == node.Value))
{
return root;
}
else
{
Node found = FindParent(root.Right, node);
if (found == null)
{
found = FindParent(root.Left, node);
}
return found;
}
}
public static Node GetLeftMost (Node node)
{
if (node.Left == null)
{
return node;
}
return GetLeftMost(node.Left);
}
nous pouvons trouver le successeur en o(log n) sans utiliser de pointeurs parent (pour un arbre équilibré).
l'idée est très similaire à quand vous avez des pointeurs parent.
nous pouvons définir une fonction récursive qui réalise ceci comme suit:
- si le noeud courant est la cible, retourner le noeud le plus à gauche / le plus petit de son sous-arbre droit, s'il existe.
- à gauche si la cible est plus petite que le noeud courant, et juste si c'est plus grand.
- si la cible est à gauche et que nous n'avons pas encore trouvé de successeur, retourner le noeud courant.
Pseudo-code:
Key successor(Node current, Key target):
if current == null
return null
if target == current.key
if current.right != null
return leftMost(current.right).key
else
return specialKey
else
if target < current.key
s = successor(current.left, target)
if s == specialKey
return current.key
else
return s
else
return successor(current.right, target)
Node leftMost(Node current):
while current.left != null
current = current.left
return current