Mise en œuvre DE BFS, DFS et Dijkstra

Oui

disons que nous avons ce graphique, et que nous voulons trouver les distances les plus courtes à partir de A:

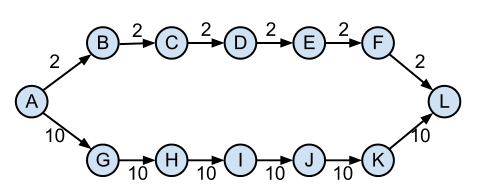
voici un simple NodeCollection interface qui permet les opérations nécessaires pour la traversée:

interface NodeCollection<E> {
    void offer(E node);
    E extract();
    boolean isEmpty();
}

et les implémentations pour la file d'attente, la pile et la file d'attente prioritaire. Notez que cette interface et les classes n'ont pas vraiment besoin d'être générique:

static class NodeQueue<E> implements NodeCollection<E> {
    private final Queue<E> queue = new LinkedList<E>();
    @Override public void offer(E node) { queue.offer(node); }
    @Override public E extract() { return queue.poll(); }
    @Override public boolean isEmpty() { return queue.isEmpty(); }
}

static class NodeStack<E> implements NodeCollection<E> {
    private final Stack<E> stack = new Stack<E>();
    @Override public void offer(E node) { stack.push(node); }
    @Override public E extract() { return stack.pop(); }
    @Override public boolean isEmpty() { return stack.isEmpty(); }
}

static class NodePriorityQueue<E> implements NodeCollection<E> {
    private final PriorityQueue<E> pq = new PriorityQueue<E>();
    @Override public void offer(E node) { pq.add(node); }
    @Override public E extract() { return pq.poll(); }
    @Override public boolean isEmpty() { return pq.isEmpty(); }
}

Notez que pour PriorityQueue pour travailler comme attendu, le Node classe doit fournir un compareTo(Node) méthode:

static class Node implements Comparable<Node> {
    final String name;
    Map<Node, Integer> neighbors;
    int dist = Integer.MAX_VALUE;
    Node prev = null;
    char color = 'w';

    Node(String name) {
        this.name = name;
        this.neighbors = Maps.newHashMap();
    }

    @Override public int compareTo(Node o) {
        return ComparisonChain.start().compare(this.dist, o.dist).result();
    }
}

voici le Graph classe. Notez que l' traverse méthode NodeCollection instance, qui sera utilisée pour stocker les noeuds lors de la traversée.

static class Graph {
    Map<String, Node> nodes = Maps.newHashMap();

    void addEdge(String fromName, String toName, int weight) {
        Node from = getOrCreate(fromName);
        Node to = getOrCreate(toName);
        from.neighbors.put(to, weight);
        to.neighbors.put(from, weight);
    }

    Node getOrCreate(String name) {
        if (!nodes.containsKey(name)) {
            nodes.put(name, new Node(name));
        }
        return nodes.get(name);
    }

    /**
     * Traverses this graph starting at the given node and returns a map of shortest paths from the start node to
     * every node.
     *
     * @param startName start node
     * @return shortest path for each node in the graph
     */
    public Map<String, Integer> traverse(String startName, NodeCollection<Node> collection) {
        assert collection.isEmpty();
        resetNodes();

        Node start = getOrCreate(startName);
        start.dist = 0;
        collection.offer(start);

        while (!collection.isEmpty()) {
            Node curr = collection.extract();
            curr.color = 'g';
            for (Node neighbor : curr.neighbors.keySet()) {
                if (neighbor.color == 'w') {
                    int thisPathDistance = curr.dist + curr.neighbors.get(neighbor);
                    if (thisPathDistance < neighbor.dist) {
                        neighbor.dist = thisPathDistance;
                        neighbor.prev = curr;
                    }
                    collection.offer(neighbor);
                }
            }
            curr.color = 'b';
        }

        Map<String, Integer> shortestDists = Maps.newTreeMap();
        for (Node node : nodes.values()) {
            shortestDists.put(node.name, node.dist);
        }
        return shortestDists;
    }

    private void resetNodes() {
        for (Node node : nodes.values()) {
            node.dist = Integer.MAX_VALUE;
            node.prev = null;
            node.color = 'w';
        }
    }
}

Enfin voici le main méthode qui traverse le même graphique 3 fois, une fois avec chacun des NodeCollection types:

private static Graph initGraph() {
    Graph graph = new Graph();
    graph.addEdge("A", "B", 2);
    graph.addEdge("B", "C", 2);
    graph.addEdge("C", "D", 2);
    graph.addEdge("D", "E", 2);
    graph.addEdge("E", "F", 2);
    graph.addEdge("F", "L", 2);

    graph.addEdge("A", "G", 10);
    graph.addEdge("G", "H", 10);
    graph.addEdge("H", "I", 10);
    graph.addEdge("I", "J", 10);
    graph.addEdge("J", "K", 10);
    graph.addEdge("K", "L", 10);

    return graph;
}

public static void main(String[] args) {
    Graph graph = initGraph();
    System.out.println("Queue (BFS):\n" + graph.traverse("A", new NodeQueue<Node>()));
    System.out.println("Stack (DFS):\n" + graph.traverse("A", new NodeStack<Node>()));
    System.out.println("PriorityQueue (Dijkstra):\n" + graph.traverse("A", new NodePriorityQueue<Node>()));
}

Et les résultats!

Queue (BFS):
{A=0, B=2, C=4, D=6, E=8, F=10, G=10, H=20, I=30, J=40, K=22, L=12}
Stack (DFS):
{A=0, B=2, C=4, D=66, E=64, F=62, G=10, H=20, I=30, J=40, K=50, L=60}
PriorityQueue (Dijkstra):
{A=0, B=2, C=4, D=6, E=8, F=10, G=10, H=20, I=30, J=32, K=22, L=12}

notez que la DSV prend parfois la branche supérieure en premier, donnant des résultats différents mais symétriques.

voici à quoi ressemblent les résultats sur le graphique:

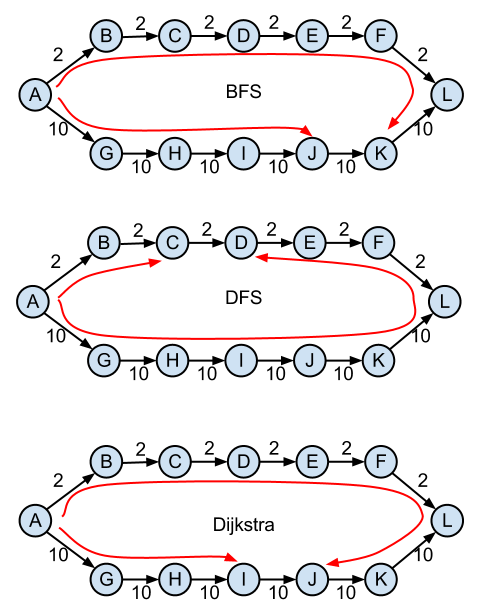
sur la question DE BFS vs. DFS: oui et non, mais plus "non"que " oui".

Si tout ce qui vous intéresse est le ordre de traversée avant, c'est à dire l'ordre dans lequel l'algorithme découvre les nouveaux sommets du graphe, alors oui: vous pouvez prendre l'algorithme classique BFS, remplacer la file D'attente FIFO par la pile LIFO, et vous obtiendrez l'algorithme pseudo-DFS.

Cependant, je l'appelle pseudo-DFS algorithme car il n'est pas vraiment la même chose que la DFS classique.

l'algorithme DFS obtenu de cette façon va effectivement générer de véritables DFS sommet de la découverte de commande. Cependant, elle sera encore différente de la DFS classique dans d'autres regadrs. Vous pouvez trouver la description de la DFS classique dans n'importe quel livre sur les algorithmes (ou Wikipedia) et vous verrez que la structure de l'algorithme est sensiblement différente de BFS. Il est fait de cette façon pour une raison. Le DFS classique offre quelques avantages supplémentaires en plus de produire le bon DFS sommet de la découverte de commande. Ces avantages supplémentaires incluent

• plus faible consommation de mémoire de pointe. dans l'implémentation DFS classique, la taille de la pile à chaque moment dans le temps est égale à la longueur du chemin entre l'origine de la recherche et le vertex courant. Dans les pseudo-DFS, la taille de la pile à chaque moment dans le temps est égale à la somme des degrés de tous les sommets, de l'origine de la recherche au sommet courant. Cela signifie que la mémoire de pointe la consommation de pseudo-algorithme DFS sera potentiellement beaucoup plus élevée.

  pour un exemple extrême, considérons un graphe "flocon de neige" constitué d'un seul sommet au centre directement relié à un 1000 sommets l'entourant. Un DFS classique traverse ce graphique avec une profondeur de pile maximale de 1. Pendant ce temps, un pseudo-DFS commencera par pousser tous les 1000 sommets dans la pile (à la manière DE BFS), ce qui donnera une profondeur de crête de la pile de 1000. C'est tout un différence.

• retour en arrière. un algorithme classique de DFS est un véritable algorithme récursif. Comme un algorithme récursif en plus du avant ordre transversal( i.e. ordre de découverte du sommet), il vous fournit aussi en arrière ordre transversal (retour en arrière). Dans le DFS classique vous visitez chaque vertex à plusieurs reprises: d'abord lorsque vous le découvrez pour la première fois, puis lorsque vous revenez d'un de ses les sommets descendants pour passer au sommet descendant suivant, et enfin pour la toute dernière fois quand vous avez traité tous ses descendants. De nombreux algorithmes basés sur la DFS sont basés sur la capture et la gestion de ces visites. Par exemple, l'algorithme de tri topologique est DFS classique qui affiche les sommets dans l'ordre de leur dernière visite DFS. L'algorithme pseudo-DFS, comme je l'ai dit plus haut, ne vous fournit qu'un accès clair au premier événement( vertex discovery), mais n'enregistre aucune mandature événements.

Oui, c'est vrai. Beaucoup d'algorithmes utiles ont des modèles similaires. Par exemple, pour les vecteurs propres des graphes, l'algorithme D'itération de puissance, si vous changez le vecteur de départ, et le vecteur d'orthogonalisation, vous obtenez toute une famille d'algorithmes utiles, mais connexes. Dans ce cas, ça s'appelle projection ABS.

dans ce cas, ils sont tous construits sur la primitive "addition incrémentielle"à un arbre. C'est juste la façon dont nous choisissons que le bord / sommet à ajouter détermine le type d'arbre et d'où le type de navigation.