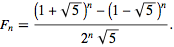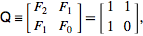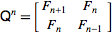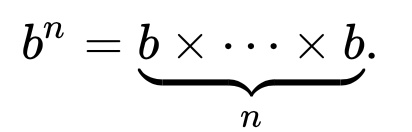Comment écrire la séquence de Fibonacci?
à l'origine, j'avais mal codé le programme. Au lieu de retourner les nombres de Fibonacci entre une gamme (ie. startNumber 1, endNumber 20 = uniquement les numéros entre 1 et 20), j'ai écrit pour le programme pour l'affichage de tous les nombres de Fibonacci entre une gamme (ie. startNumber 1, endNumber 20 affiche = 20 Premiers nombres de Fibonacci). Je pensais avoir un code de tir sûr. Aussi je ne vois pas pourquoi ce qui se passe.
startNumber = int(raw_input("Enter the start number here "))
endNumber = int(raw_input("Enter the end number here "))
def fib(n):
if n < 2:
return n
return fib(n-2) + fib(n-1)
print map(fib, range(startNumber, endNumber))
Quelqu'un a souligné dans ma partie II (qui a été fermé pour être un duplicata - https://stackoverflow.com/questions/504193/how-to-write-the-fibonacci-sequence-in-python-part-ii ) que je dois passer le startNumber et le endNumber à travers un générateur en utilisant une boucle while. Quelqu'un peut-il svp m'indiquer la direction sur la façon de faire cela? Toute aide est la bienvenue.
Je me demande d'écrire un programme qui computera et affichera la séquence de Fibonacci par un utilisateur entrant le numéro de début et le numéro de fin (c.-à-d. startNumber = 20 endNumber = 100 et il n'affichera que les nombres entre cette fourchette). Le truc est de l'utiliser de façon inclusive (ce que je ne sais pas faire en Python? - Je suppose que cela signifie d'utiliser un large éventail?).
ce que j'ai jusqu'à présent n'est pas un codage réel mais plutôt:
- Écrire Fib séquence de formule à l'infini
- afficher le numéro de début à la fin seulement à partir de la séquence Fib.
Je ne sais pas par où commencer et je demande des idées ou des idées sur la façon d'écrire ceci. J'ai aussi essayé d'écrire le Fib séquence forumla mais je me suis perdu.
30 réponses
il y a beaucoup d'informations sur la séquence de Fibonacci sur wikipedia et sur wolfram . Beaucoup plus que vous pourriez avoir besoin. Quoi qu'il en soit, il est bon d'apprendre à utiliser ces ressources pour trouver (rapidement si possible) ce dont vous avez besoin.
Écrire Fib séquence de formule à l'infini
En mathématiques, il est donné sous une forme récursive:
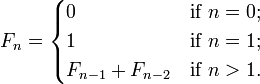
en programmation, infinite n'existe pas. Vous pouvez utiliser une forme récursive traduisant la forme mathématique directement dans votre langue, par exemple en Python elle devient:
def F(n):
if n == 0: return 0
elif n == 1: return 1
else: return F(n-1)+F(n-2)
essayez-le dans votre langue préférée et voyez que ce formulaire nécessite beaucoup de temps que n devient plus grand. En fait, C'est O(2 n ) dans le temps.
allez sur les sites que je vous ai liés et allez voir ceci (sur wolfram ):
celui-ci est assez facile à mettre en œuvre et très, très rapide à calculer, en Python:
from math import sqrt
def F(n):
return ((1+sqrt(5))**n-(1-sqrt(5))**n)/(2**n*sqrt(5))
une autre façon de le faire est de suivre la définition (de wikipedia ):
le premier numéro de la séquence est 0, le deuxième nombre est 1, et chacun le nombre est égal à la somme des deux numéros précédents du séquence elle-même, cédant la séquence 0, 1, 1, 2, 3, 5, 8, etc.
si votre langue supporte des itérateurs, vous pouvez faire quelque chose comme:
def F():
a,b = 0,1
while True:
yield a
a, b = b, a + b
afficher le numéro de début à la fin seulement à partir de la séquence Fib.
une fois que vous savez comment générer des nombres de Fibonacci, vous n'avez qu'à les parcourir et vérifier s'ils vérifier les conditions données.
supposons maintenant que vous avez écrit un f (n) qui renvoie le N-ème terme de la séquence de Fibonacci (comme celui avec sqrt(5))
dans la plupart des langues, vous pouvez faire quelque chose comme:
def SubFib(startNumber, endNumber):
n = 0
cur = f(n)
while cur <= endNumber:
if startNumber <= cur:
print cur
n += 1
cur = f(n)
en python j'utiliserais la forme iterator et je dirais:
def SubFib(startNumber, endNumber):
for cur in F():
if cur > endNumber: return
if cur >= startNumber:
yield cur
for i in SubFib(10, 200):
print i
Mon conseil est de apprendre à lire ce dont vous avez besoin. Projet Euler (google) va vous former à faire so: P Bonne chance et amusez-vous!
générateur pythonique efficace de la séquence de Fibonacci
j'ai trouvé cette question en essayant d'obtenir la génération pythonique la plus courte de cette séquence (plus tard réalisant que j'avais vu une semblable dans un proposition D'amélioration de Python ), et je n'ai pas remarqué quelqu'un d'autre venir avec ma solution spécifique (bien que la réponse supérieure se rapproche, mais encore moins élégant), donc ici, avec des commentaires décrivant la première itération, parce que je pensez que cela peut aider les lecteurs à comprendre:
def fib():
a, b = 0, 1
while True: # First iteration:
yield a # yield 0 to start with and then
a, b = b, a + b # a will now be 1, and b will also be 1, (0 + 1)
et usage:
for index, fibonacci_number in zip(range(10), fib()):
print('{i:3}: {f:3}'.format(i=index, f=fibonacci_number))
imprime:
0: 0
1: 1
2: 1
3: 2
4: 3
5: 5
6: 8
7: 13
8: 21
9: 34
10: 55
(à des fins d'attribution, j'ai récemment remarqué une implémentation similaire dans la documentation Python sur les modules, même en utilisant les variables a et b , que je me souviens avoir vu avant d'écrire cette réponse. Mais je pense que cette réponse démontre une meilleure utilisation de la langue.)
définie de manière Récursive mise en œuvre
Le Online Encyclopedia of Integer sequences définit la Séquence de Fibonacci de manière récursive comme
F (n) = F (n-1) + F (n-2) avec F (0) = 0 et F (1) = 1
définition succincte de cette récursivité en Python peut être fait comme suit:
def rec_fib(n):
'''inefficient recursive function as defined, returns Fibonacci number'''
if n > 1:
return rec_fib(n-1) + rec_fib(n-2)
return n
mais ce la représentation exacte de la définition mathématique est incroyablement inefficace pour des nombres beaucoup plus grands que 30, parce que chaque nombre étant calculé doit également calculer pour chaque nombre au-dessous de lui. Vous pouvez démontrer sa lenteur en utilisant ce qui suit:
for i in range(40):
print(i, rec_fib(i))
Memoized la récursivité pour plus d'efficacité
il peut être memoizé pour améliorer la vitesse (cet exemple tire avantage du fait qu'un argument de mot-clé par défaut est le même objet chaque fois que la fonction est appelée, mais normalement vous ne voudriez pas utiliser une mutable argument par défaut pour cette raison):
def mem_fib(n, _cache={}):
'''efficiently memoized recursive function, returns a Fibonacci number'''
if n in _cache:
return _cache[n]
elif n > 1:
return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
return n
vous trouverez la version memoized est beaucoup plus rapide, et dépassera rapidement votre profondeur maximale de récursion avant que vous ne pouvez même penser à se lever pour le café. Vous pouvez voir à quel point il est plus rapide visuellement en faisant ceci:
for i in range(40):
print(i, mem_fib(i))
(il peut sembler que nous pouvons juste faire le ci-dessous, mais en fait il ne nous permet pas de profiter du cache, parce qu'il s'appelle lui-même avant que setdefault ne soit appelé.)
def mem_fib(n, _cache={}):
'''don't do this'''
if n > 1:
return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
return n
générateur défini de façon récursive:
comme J'ai appris Haskell, je suis tombé sur cette mise en œuvre à Haskell:
fib@(0:tfib) = 0:1: zipWith (+) fib tfib
le plus proche je pense que je peux obtenir à ce en Python en ce moment est:
from itertools import tee
def fib():
yield 0
yield 1
# tee required, else with two fib()'s algorithm becomes quadratic
f, tf = tee(fib())
next(tf)
for a, b in zip(f, tf):
yield a + b
cela le démontre:
[f for _, f in zip(range(999), fib())]
il ne peut aller jusqu'à la limite de la récursivité. Habituellement, 1000, alors que la version Haskell peut aller jusqu'à 100s de millions, bien qu'il utilise les 8 Go de la mémoire de mon ordinateur portable pour le faire:
> length $ take 100000000 fib
100000000
Pourquoi ne pas simplement faire ce qui suit?
x = [1,1]
for i in range(2, 10):
x.append(x[-1] + x[-2])
print(', '.join(str(y) for y in x))
l'idée derrière la séquence de Fibonacci est montrée dans le code Python suivant:
def fib(n):
if n == 1:
return 1
elif n == 0:
return 0
else:
return fib(n-1) + fib(n-2)
cela signifie que fib est une fonction qui peut faire l'une des trois choses. Il définit fib(1) == 1, fib(0) == 0, et fib(n):
fib(n-1) + fib (n-2)
Où n est un entier arbitraire. Cela signifie que fib(2) par exemple, se développe à l'arithmétique suivante:
fib(2) = fib(1) + fib(0)
fib(1) = 1
fib(0) = 0
# Therefore by substitution:
fib(2) = 1 + 0
fib(2) = 1
on peut calculer fib (3) de la même façon que pour le calcul indiqué ci-dessous:
fib(3) = fib(2) + fib(1)
fib(2) = fib(1) + fib(0)
fib(2) = 1
fib(1) = 1
fib(0) = 0
# Therefore by substitution:
fib(3) = 1 + 1 + 0
la chose importante à réaliser ici est que fib(3) ne peut pas être calculé sans calculer fib(2), qui est calculé en connaissant les définitions de fib(1) et fib(0). Avoir une fonction qui s'appelle elle-même comme la fonction fibonacci le fait est appelé récursion, et c'est un sujet important dans la programmation.
cela ressemble à un devoir, donc je ne vais pas faire la partie début / fin pour vous. Python est un langage merveilleusement expressif pour cela cependant, donc cela devrait avoir du sens si vous comprenez les mathématiques, et nous espérons vous enseigner sur la récursion. Bonne chance!
Edit: une critique potentielle de mon code est qu'il n'utilise pas la fonction Python de rendement super-maniable, ce qui rend la fonction fib(n) Beaucoup plus courte. Mon exemple est un peu plus générique cependant, puisque peu de langues en dehors de Python ont réellement du rendement.
complexité temporelle:
la caractéristique de mise en cache réduit la façon normale de calculer la série de Fibonacci de O (2^n) à O (n) en éliminant les répétitions dans l'arbre récursif de la série de Fibonacci:
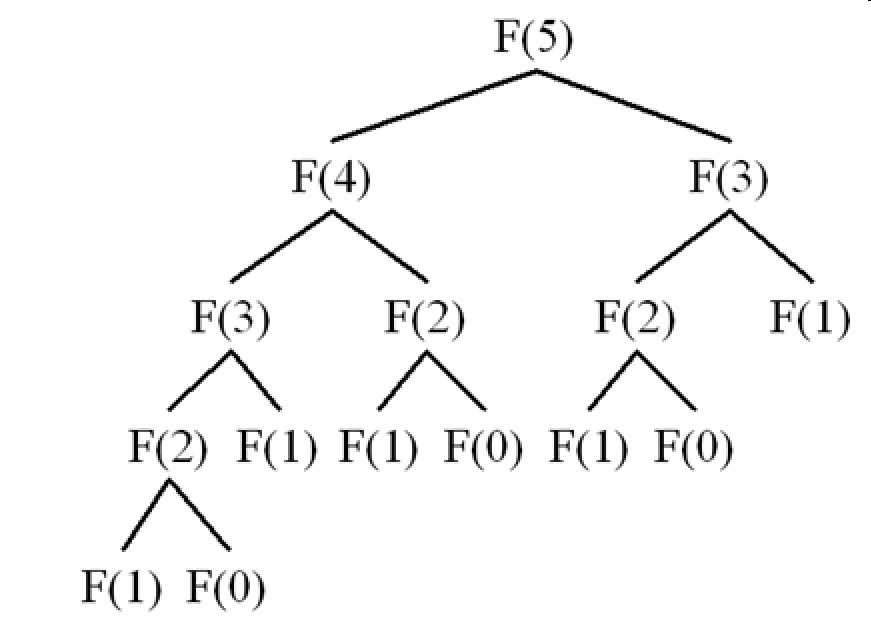
Code:
import sys
table = [0]*1000
def FastFib(n):
if n<=1:
return n
else:
if(table[n-1]==0):
table[n-1] = FastFib(n-1)
if(table[n-2]==0):
table[n-2] = FastFib(n-2)
table[n] = table[n-1] + table[n-2]
return table[n]
def main():
print('Enter a number : ')
num = int(sys.stdin.readline())
print(FastFib(num))
if __name__=='__main__':
main()
c'est assez efficace, en utilisant O(log n) opérations arithmétiques de base.
def fib(n):
return pow(2 << n, n + 1, (4 << 2*n) - (2 << n) - 1) % (2 << n)
celui-ci utilise O(1) opérations arithmétiques de base, mais la taille des résultats intermédiaires est grande et donc pas du tout efficace.
def fib(n):
return (4 << n*(3+n)) // ((4 << 2*n) - (2 << n) - 1) & ((2 << n) - 1)
celui - ci calcule X^n dans le cycle polynomial Z[X] / (X^2 - X-1) en utilisant l'exponentiation par quadrature. Le résultat de ce calcul est le polynôme Fib(n)X + Fib(n-1), à partir duquel le nième Fibonacci le numéro peut être lu.
encore une fois, cela utilise O(log n) opérations arithmétiques et est très efficace.
def mul(a, b):
return a[0]*b[1]+a[1]*b[0]+a[0]*b[0], a[0]*b[0]+a[1]*b[1]
def fib(n):
x, r = (1, 0), (0, 1)
while n:
if n & 1: r = mul(r, x)
x = mul(x, x)
n >>= 1
return r[0]
code Python canonique pour imprimer la séquence de Fibonacci:
a,b=1,1
while(True):
print a,
a,b=b,a+b # Could also use b=a+b;a=b-a
Pour le problème de "Impression le premier nombre de Fibonacci de plus de 1000 chiffres":
a,b=1,1
i=1
while(len(str(a))<=1000):
i=i+1
a,b=b,a+b
print i,len(str(a)),a
utiliser pour boucle et imprimer juste le résultat
def fib(n:'upto n number')->int:
if n==0:
return 0
elif n==1:
return 1
a=0
b=1
for i in range(0,n-1):
b=a+b
a=b-a
return b
résultat
>>>fib(50)
12586269025
>>>>
>>> fib(100)
354224848179261915075
>>>
imprimer le list contenant tous les numéros
def fib(n:'upto n number')->int:
l=[0,1]
if n==0:
return l[0]
elif n==1:
return l
a=0
b=1
for i in range(0,n-1):
b=a+b
a=b-a
l.append(b)
return l
résultat
>>> fib(10)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
il y a une méthode très simple pour réaliser cela!
vous pouvez exécuter ce code en ligne gratuitement en utilisant http://www.learnpython.org /
# Set the variable brian on line 3!
def fib(n):
"""This is documentation string for function. It'll be available by fib.__doc__()
Return a list containing the Fibonacci series up to n."""
result = []
a = 0
b = 1
while a < n:
result.append(a) # 0 1 1 2 3 5 8 (13) break
tmp_var = b # 1 1 2 3 5 8 13
b = a + b # 1 2 3 5 8 13 21
a = tmp_var # 1 1 2 3 5 8 13
# print(a)
return result
print(fib(10))
# result should be this: [0, 1, 1, 2, 3, 5, 8]
use récursion:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
x=input('which fibonnaci do you want?')
print fib(x)
nous savons que
et que la puissance n-e de cette matrice nous donne:
donc nous pouvons implémenter une fonction qui calcule simplement la puissance de cette matrice à la puissance n-th -1.
comme tout ce que nous savons, la puissance est égale à
ainsi à la fin la fonction fibonacci serait O( n )... rien de vraiment différent d'une mise en œuvre plus facile si ce n'était pas pour le fait que nous savons aussi que x^n * x^n = x^2n et l'évaluation de x^n peut donc être fait avec la complexité O( log n )
Voici mon implémentation fibonacci en utilisant le langage de programmation swift:
struct Mat {
var m00: Int
var m01: Int
var m10: Int
var m11: Int
}
func pow(m: Mat, n: Int) -> Mat {
guard n > 1 else { return m }
let temp = pow(m: m, n: n/2)
var result = matMultiply(a: temp, b: temp)
if n%2 != 0 {
result = matMultiply(a: result, b: Mat(m00: 1, m01: 1, m10: 1, m11: 0))
}
return result
}
func matMultiply(a: Mat, b: Mat) -> Mat {
let m00 = a.m00 * b.m00 + a.m01 * b.m10
let m01 = a.m00 * b.m01 + a.m01 * b.m11
let m10 = a.m10 * b.m00 + a.m11 * b.m10
let m11 = a.m10 * b.m01 + a.m11 * b.m11
return Mat(m00: m00, m01: m01, m10: m10, m11: m11)
}
func fibonacciFast(n: Int) -> Int {
guard n > 0 else { return 0 }
let m = Mat(m00: 1, m01: 1, m10: 1, m11: 0)
return pow(m: m, n: n-1).m00
}
complexité O (log n). Nous calculons la puissance de Q avec l'exposant n-1 et ensuite nous prenons l'élément m00 qui est Fn+1 qui à la puissance exposant n-1 est exactement le N-ème nombre de Fibonacci que nous voulions.
une fois que vous avez la fonction fibonacci rapide, vous pouvez itérer à partir du nombre de début et de fin pour obtenir la partie de la séquence de Fibonacci qui vous intéresse.
let sequence = (start...end).map(fibonacciFast)
bien sûr d'abord effectuer un certain contrôle sur le début et la fin pour s'assurer qu'ils peuvent former une plage valide.
je sais que la question a 8 ans, mais j'ai quand même eu du plaisir à y répondre. :)
def fib():
a,b = 1,1
num=eval(input("Please input what Fib number you want to be calculated: "))
num_int=int(num-2)
for i in range (num_int):
a,b=b,a+b
print(b)
Ces air un peu plus compliquées qu'elles ne devraient l'être. Mon code est très simple et rapide:
def fibonacci(x):
List = []
f = 1
List.append(f)
List.append(f) #because the fibonacci sequence has two 1's at first
while f<=x:
f = List[-1] + List[-2] #says that f = the sum of the last two f's in the series
List.append(f)
else:
List.remove(List[-1]) #because the code lists the fibonacci number one past x. Not necessary, but defines the code better
for i in range(0, len(List)):
print List[i] #prints it in series form instead of list form. Also not necessary
une autre façon de le faire:
a,n=[0,1],10
map(lambda i: reduce(lambda x,y: a.append(x+y),a[-2:]),range(n-2))
Affectation de liste aux "a", l'attribution entier "n" Map et reduce sont deux des trois fonctions les plus puissantes de python. Ici la carte est utilisée juste pour itérer' n-2 ' fois. un[-2:] aura le dernier deux éléments d'un tableau. A. ajouter (x+y) ajoutera les deux derniers éléments et ajoutera au tableau
OK.. après avoir été fatigué de faire référence à toutes les réponses longues, maintenant trouver le tri ci-dessous et douce, assez simple pour mettre en œuvre Fibonacci en python. Vous pouvez l'améliorer de la façon que vous voulez en obtenant un argument ou en obtenant l'entrée d'utilisateur...ou changer les limites de 10000. Comme vous en avez besoin......
def fibonacci():
start = 0
i = 1
lt = []
lt.append(start)
while start < 10000:
start += i
lt.append(start)
i = sum(lt[-2:])
lt.append(i)
print "The Fibonaccii series: ", lt
cette approche donne également de bons résultats. Trouver les statistiques d'exécution ci-dessous
In [10]: %timeit fibonacci
10000000 loops, best of 3: 26.3 ns per loop
import time
start_time = time.time()
#recursive solution
def fib(x, y, upperLimit):
return [x] + fib(y, (x+y), upperLimit) if x < upperLimit else [x]
#To test :
print(fib(0,1,40000000000000))
print("run time: " + str(time.time() - start_time))
résultats
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853]
durée: 0.04298138618469238
essentiellement traduit de Ruby:
def fib(n):
a = 0
b = 1
for i in range(1,n+1):
c = a + b
print c
a = b
b = c
...
def fib(lowerbound, upperbound):
x = 0
y = 1
while x <= upperbound:
if (x >= lowerbound):
yield x
x, y = y, x + y
startNumber = 10
endNumber = 100
for fib_sequence in fib(startNumber, endNumber):
print "And the next number is... %d!" % fib_sequence
suite de Fibonacci est: 1, 1, 2, 3, 5, 8, ... .
C'est-à-dire f(1) = 1 , f(2) = 1 , f(3) = 2 , ... , f(n) = f(n-1) + f(n-2) .
mon implémentation préférée (la plus simple et pourtant atteint une vitesse de lumière par rapport à d'autres implémentations) est celle-ci:
def fibonacci(n):
a, b = 0, 1
for _ in range(1, n):
a, b = b, a + b
return b
Test
>>> [fibonacci(i) for i in range(1, 10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34]
"1519160920 de" Timing
>>> %%time
>>> fibonacci(100**3)
CPU times: user 9.65 s, sys: 9.44 ms, total: 9.66 s
Wall time: 9.66 s
Edit: un exemple de visualisation pour cette mise en œuvre.
la récursion ajoute du temps. Pour éliminer les boucles, d'abord import math . Ensuite, utilisez math.sqrt et ratio d'or dans une fonction:
#!/usr/bin/env python3
import math
def fib(n):
gr = (1 + math.sqrt(5)) / 2
fib_first = (gr**n - (1 - gr)**n) / math.sqrt(5)
return int(round(fib_first))
fib_final = fib(100)
print(fib_final)
c'est une amélioration à la réponse de mathew henry:
def fib(n):
a = 0
b = 1
for i in range(1,n+1):
c = a + b
print b
a = b
b = c
le code doit être imprimé b au lieu de c
sortie: 1,1,2,3,5 ....
C'est la plus simple en python pour les séries de Fibonacci mais ajustée [0] dans le tableau de sortie par append() pour aboutir à la deuxième variable de la liste de résultats qui est result.append(second)
def fibo(num):
first = 0
second = 1
result = [0]
print('Fibonacci series is')
for i in range(0,num):
third = first + second
#print(second)
result.append(second)
first = second
second = third
print(result)
return
fibo(7)
sortie
Fibonacci series is
[0, 1, 1, 2, 3, 5, 8, 13]
allez trouver comment convertir un problème récursif en un problème itératif. On devrait pouvoir calculer à partir de là.
Que pourraient être les principes qu'ils essayent de vous apprendre, surtout si c'est un des Algorithmes de parcours.
15 minutes après un tutoriel que j'ai utilisé lors de L'apprentissage de Python, il a demandé au lecteur d'écrire un programme qui calculerait une séquence de Fibonacci à partir de 3 numéros d'entrée (premier numéro de Fibonacci, deuxième numéro, et numéro auquel arrêter la séquence). Le tutoriel ne couvrait que les variables, if/thens, et les boucles jusqu'à ce point. Pas de fonctions encore. J'ai trouvé le code suivant:
sum = 0
endingnumber = 1
print "\n.:Fibonacci sequence:.\n"
firstnumber = input("Enter the first number: ")
secondnumber = input("Enter the second number: ")
endingnumber = input("Enter the number to stop at: ")
if secondnumber < firstnumber:
print "\nSecond number must be bigger than the first number!!!\n"
else:
while sum <= endingnumber:
print firstnumber
if secondnumber > endingnumber:
break
else:
print secondnumber
sum = firstnumber + secondnumber
firstnumber = sum
secondnumber = secondnumber + sum
comme vous pouvez le voir, c'est vraiment inefficace, mais ça marche.
passer à travers http://projecteuler.net/problem=2 c'était mon prendre sur elle
# Even Fibonacci numbers
# Problem 2
def get_fibonacci(size):
numbers = [1,2]
while size > len(numbers):
next_fibonacci = numbers[-1]+numbers[-2]
numbers.append(next_fibonacci)
print numbers
get_fibonacci(20)
def fib(x, y, n):
if n < 1:
return x, y, n
else:
return fib(y, x + y, n - 1)
print fib(0, 1, 4)
(3, 5, 0)
#
def fib(x, y, n):
if n > 1:
for item in fib(y, x + y, n - 1):
yield item
yield x, y, n
f = fib(0, 1, 12)
f.next()
(89, 144, 1)
f.next()[0]
55
c'était un devoir de pratique que J'ai vu sur le Sal de Khan Academy sur la programmation Python: https://www.khanacademy.org/science/computer-science-subject/computer-science/v/exercise---write-a-fibonacci-function
Il n'est probablement pas la première personne à céder que peu de travail à faire. Mais c'est génial de le découvrir tout seul. J'ai beaucoup appris à le comprendre et c'était génial.
je vous recommande débrouillez-vous avant d'essayer de copier le code de quelqu'un d'autre pour vos devoirs.
dans la vidéo ci-dessus, Sal l'instructeur, montre toute la théorie derrière le nombre de Fibonacci, et avec cela à l'Esprit, vous devriez être en mesure de comprendre.
cela m'a pris environ 10 minutes et c'est le code que j'ai créé (j'apprends Python depuis 3 jours et c'est mon premier langage de programmation À APPRENDRE). Je n'aurais pas pu écrire le code s'il n'était pas pour la vidéo du tutoriel avant: https://www.khanacademy.org/science/computer-science-subject/computer-science/v/comparing-iterative-and-recursive-factorial-functions que l'on donne un exemple de Sal faisant une équation factorielle récursive et vous donne l'état d'esprit pour résoudre ce problème.
Voici mon code:
def fibonacci(num):
if num <= 1: #base case
return num
else:
return fibonacci(num-1) + fibonacci(num-2)
Vous pouvez voir que si le nombre est 1 ou 0, puis vous retournez simplement le nombre.
je trouve cela plus propre que de dire si le nombre est 1 retourner 1 et si le nombre est 0 retourner 0.
peut-être que cela aidera
def fibo(n):
result = []
a, b = 0, 1
while b < n:
result.append(b)
a, b = b, b + a
return result
essayez ceci:
def nth_fib(n):
if n == 0:
return 1
elif n == 1:
return 0
else:
return nth_fib(n - 1) + nth_fib(n - 2)
basé sur la séquence classique de fibonacci et juste pour le bien des monocouches
si vous avez juste besoin du numéro de l'index, vous pouvez utiliser le réduire (même si réduire il n'est pas mieux adapté pour cela, il peut être un bon exercice)
def fibonacci(index):
return reduce(lambda r,v: r.append(r[-1]+r[-2]) or (r.pop(0) and 0) or r , xrange(index), [0, 1])[1]
et pour obtenir le tableau complet il suffit de supprimer le ou (r. pop (0) et 0)
reduce(lambda r,v: r.append(r[-1]+r[-2]) or r , xrange(last_index), [0, 1])